10th Standard Nirdeshanka Rekhaganita Notes Question Answer Guide Extract Mcq Pdf Download Kannada Medium Karnataka State Syllabus 2025,10ನೇ ತರಗತಿ ಗಣಿತ ನಿರ್ದೇಶಾಂಕ ರೇಖಾಗಣಿತ ನೋಟ್ಸ್, 10th Class Nirdeshanka Rekhaganita Notes, 10th Standard Nirdeshanka Rekhaganita PDF,10th Standard Nirdeshanka Rekhaganita Question and Answer, 10th Standard Maths Kannada Medium Notes,10ನೇ ತರಗತಿ ಗಣಿತ ನಿರ್ದೇಶಾಂಕ ರೇಖಾಗಣಿತ, 10ನೇ ತರಗತಿ ಗಣಿತ ನಿರ್ದೇಶಾಂಕ ರೇಖಾಗಣಿತ ನೋಟ್ಸ್ PDF, 10th Standard Nirdeshanka Rekhaganita Notes 2025, ನಿರ್ದೇಶಾಂಕ ರೇಖಾಗಣಿತ 10ನೇ ತರಗತಿ, kseeb solutions for class 10 maths chapter 7 notes, maths notes for class 10 pdf.
ಘಟಕ 07 – ನಿರ್ದೇಶಾಂಕ ರೇಖಾಗಣಿತ
ಅಭ್ಯಾಸ 7.1
1). ಕೆಳಗಿನ ಬಿಂದುಗಳ ಜೋಡಿಗಳ ನಡುವಿನ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
i) (2, 3), (4, 1)
ii) (-5, 7), (-1, 3)
iii) (a, b), (-a, -b)
ಉತ್ತರ:
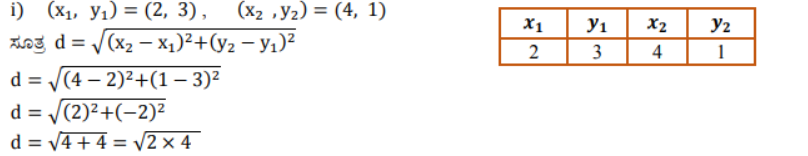
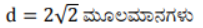
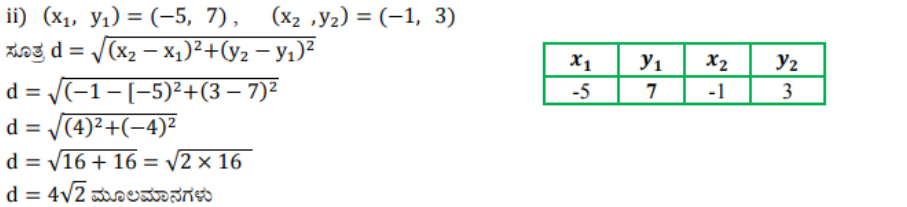
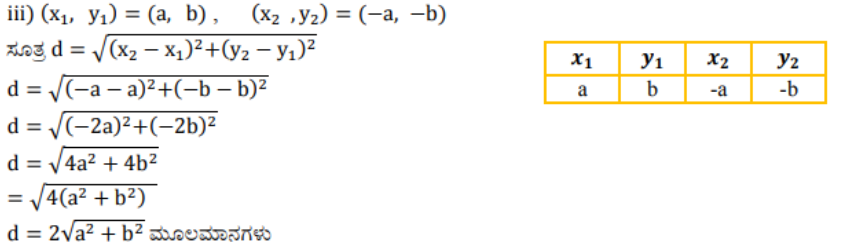
2). (0, 0) ಮತ್ತು (36, 15) ಬಿಂದುಗಳ ನಡುವಿನ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ನಿಮಗೀಗ, ವಿಭಾಗ 7.2 ರಲ್ಲಿ ಚರ್ಚಿಸಲಾದ P ಮತ್ತು Q ನಗರಗಳ ನಡುವಿನ ಅಂತರವನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದೆ?
ಉತ್ತರ:
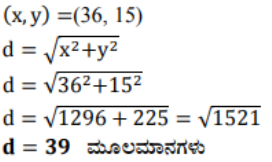
3). (1, 5), (2, 3) ಮತ್ತು (-2, -11) ಎಂಬ ಬಿಂದುಗಳು ಸರಳರೇಖಾಗತವೇ ಎಂದು ನಿರ್ಣಯಿಸಿ.
ಉತ್ತರ:

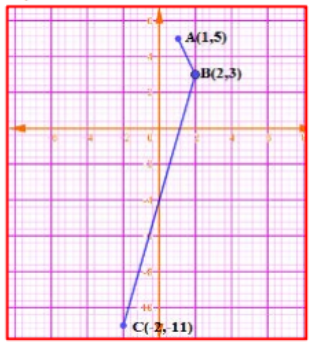
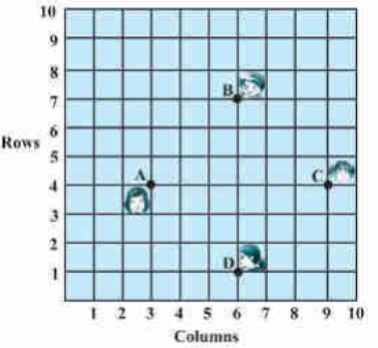
4). (5, -2), (6, 4) ಮತ್ತು (7, -2) ಒಂದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜದ ಶೃಂಗ ಬಿಂದುಗಳಾಗಿವೆಯೇ ಎಂದು ಪರಿಶೀಲಿಸಿ.
ಉತ್ತರ:
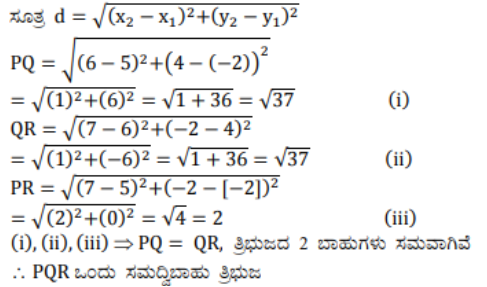
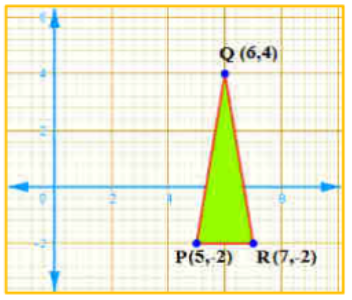
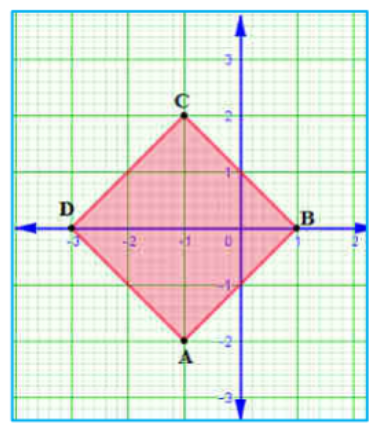
5) ಒಂದು ತರಗತಿಯಲ್ಲಿ ನಾಲ್ಕು ಮಂದಿ ಗೆಳತಿಯರು ಚಿತ್ರ 7.8 ರಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ A, B, C ಮತ್ತು D ಎಂಬ ಬಿಂದುಗಳಲ್ಲಿ ಕುಳಿತಿರುತ್ತಾರೆ. ಚಂಪಾ ಮತ್ತು ಚಮೇಲಿ ತರಗತಿಯೊಳಕ್ಕೆ ಬರುತ್ತಾರೆ. ಕೆಲವು ನಿಮಿಷ ಅವರನ್ನು ಗಮನಿಸಿದ ಬಳಿಕ ಚಂಪಾ ಚಮೇಲಿಯಲ್ಲಿ ಕೇಳುತ್ತಾಳೆ. “ABCD ಒಂದು ಚೌಕವೆಂದು ನಿನಗೆ ಅನಿಸುತ್ತಿಲ್ಲವೆ?” ಎಂದು. ಚಮೇಲಿ ಒಪ್ಪುವುದಿಲ್ಲ. ದೂರಸೂತ್ರವನ್ನು ಉಪಯೋಗಿಸಿ ಅವರಿಬ್ಬರಲ್ಲಿ ಯಾರು ಸರಿ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

6) ಕೆಳಗಿನ ಬಿಂದುಗಳಿಂದ ಚತುರ್ಭುಜಗಳು ಉಂಟಾಗುವುದಾದರೆ, ಉಂಟಾದ ಚತುರ್ಭುಜದ ವಿಧವನ್ನು ಹೆಸರಿಸಿ ಮತ್ತು ನಿಮ್ಮ ಉತ್ತರಕ್ಕೆ ಕಾರಣವನ್ನು ಕೊಡಿರಿ.
i) (-1, -2), (1, 0), (-1, 2), (-3, 0)
ii) (-3, 5), (3, 1), (0, 3), (-1, -4)
iii) (4, 5), (7, 6), (4, 3), (1, 2)
ಉತ್ತರ:
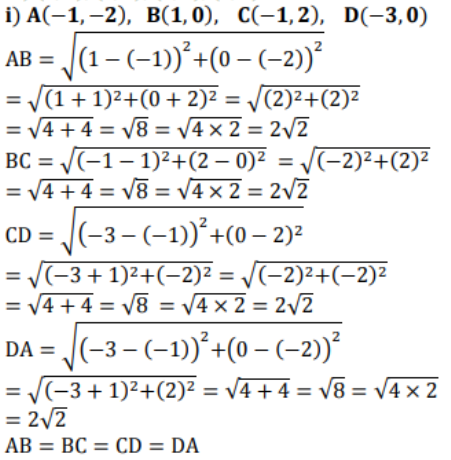
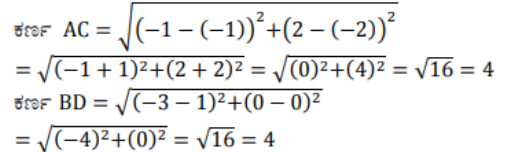
AC = BD ಎಲ್ಲಾ ಬಾಹುಗಳು ಸಮ AB = BC = CD = DA, ಕರ್ಣಗಳು ಸಮ AC = DB
ಆದ್ದರಿಂದ ABCD ಒಂದು ಚೌಕವಾಗಿದೆ.
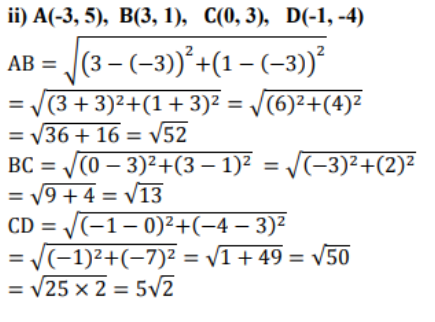
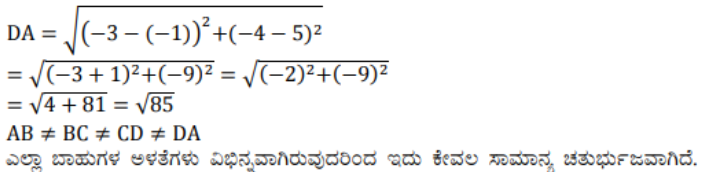
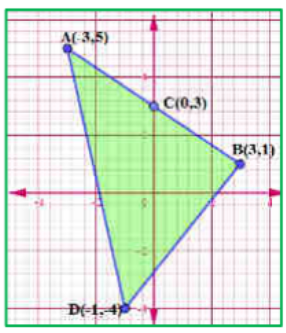
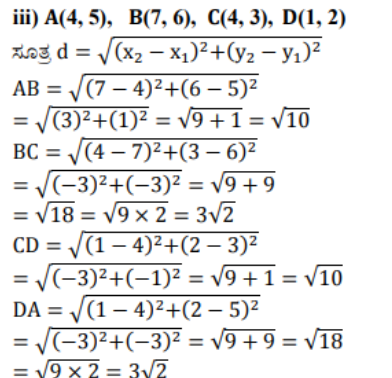
AB = CD, BC = DA
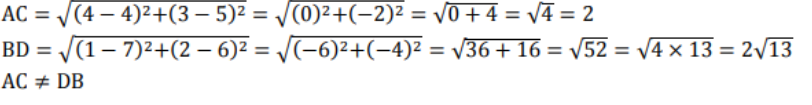
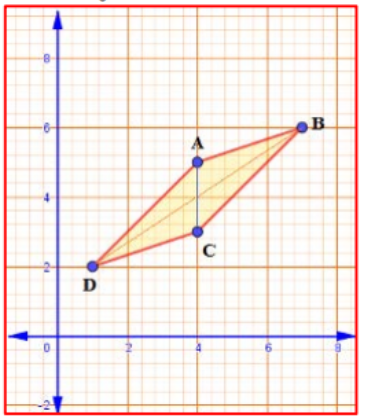
ಅಭಿಮುಖ ಬಾಹುಗಳು ಸಮ AB = CD ಮತ್ತು BC = DA
ಕರ್ಣಗಳು ಸಮವಲ್ಲ AC ≠ DB
ಆದ್ದರಿಂದ ಕೊಟ್ಟಿರುವ ಬಿಂದುಗಳು ಸಮಾಂತರ ಚತುರ್ಭುಜವನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ.
7) (2, -5) ಮತ್ತು (-2, 9) ರಿಂದ ಸಮಾನ ದೂರದಲ್ಲಿರುವ X – ಅಕ್ಷದ ಮೇಲಿನ ಬಿಂದುವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

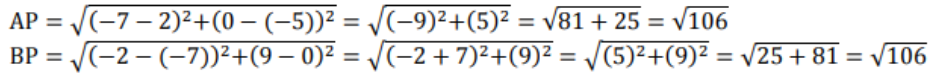
8) P (2, -3) ಮತ್ತು Q(10, y) ಬಿಂದುಗಳ ನಡುವಿನ ದೂರ 10 ಮಾನಗಳಾದರೆ, y ಯ ಬೆಲೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
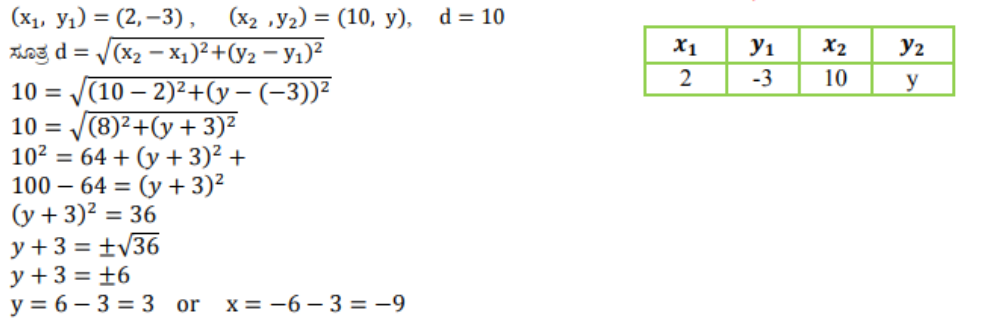
9) Q (0, 1) ಬಿಂದುವು P (5, -3) ಮತ್ತು R (x, 6) ರಿಂದ ಸಮಾನ ದೂರದಲ್ಲಿದ್ದರೆ, X ನ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. QR ಮತ್ತು PR ದೂರಗಳನ್ನು ಕೂಡಾ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
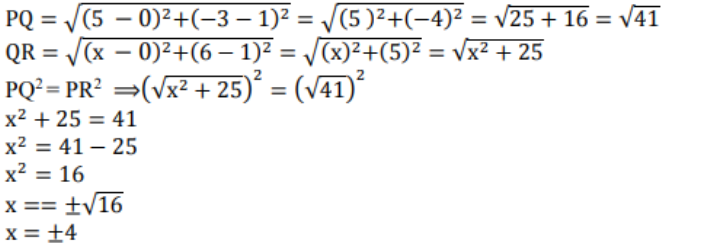
R ಬಿಂದುವಿನ ನಿರ್ದೇ ಶಾಂಕಗಳು (4,6) ಅಥವಾ (-4,6)
R ಬಿಂದುವಿನ ನಿರ್ದೇ ಶಾಂಕಗಳು (4,6) ಆದಾಗ
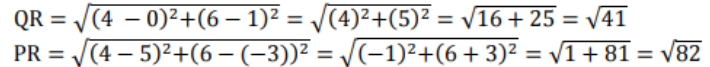
R ಬಿಂದುವಿನ ನಿರ್ದೇ ಶಾಂಕಗಳು (-4,6) ಆದಾಗ
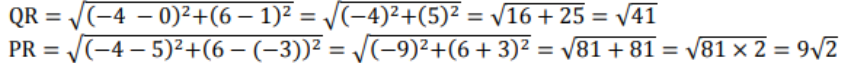
10) (x, y) ಬಿಂದುವು (3, 6) ಮತ್ತು (-3, 4) ಬಿಂದುಗಳಿಂದ ಸಮಾನ ದೂರದಲ್ಲಿದ್ದರೆ, X ಮತ್ತು y ಗಳ ನಡುವೆ ಒಂದು ಸಂಬಂಧವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

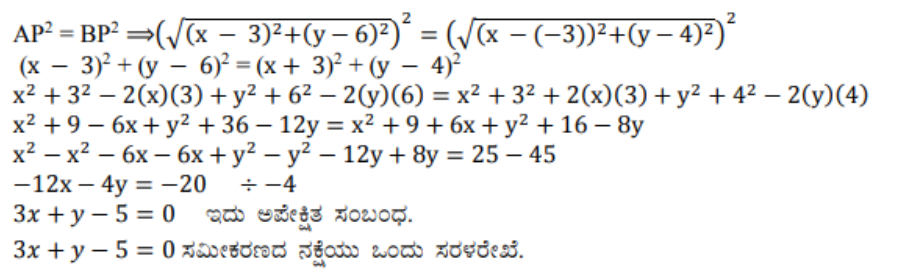
A ಮತ್ತು B ಗಳಿಂದ ಸಮಾನ ದೂರದಲ್ಲಿರುವ ಬಿಂದು AB ಯ ಲಂಬಾರ್ಧಕ ಮೇಲಿರುತ್ತದೆ.
ಅಭ್ಯಾಸ 7.2
1. (-1, 7) ಮತ್ತು (4, -3) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವನ್ನು 2 : 3 ರ ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
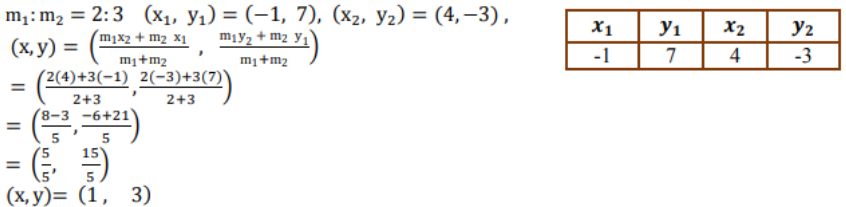
(-1, 7) ಮತ್ತು (4, -3) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವನ್ನು 2 : 3 ರ ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು (1, 3)
2) (4, -1) ಮತ್ತು (-2, -3) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡದ ತ್ರೈಭಾಜಕ ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

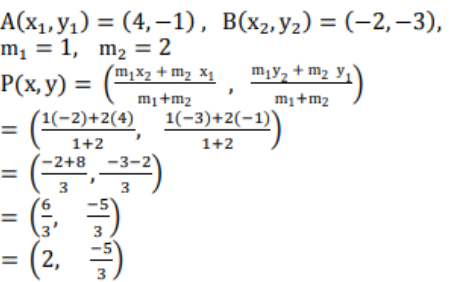
Q ಯು AB ಯನ್ನು ಆತಂರಿಕವಾಗಿ 2 : 1 ಅಮುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ ಭಾಗ ಪ್ರಮಾಣ ಸೂತ್ರವನ್ನು ವಿಭಾಗಿಸುವ ಮೂಲಕ Q ಯ ನಿರ್ದೇಶಾಂಕಗಳು
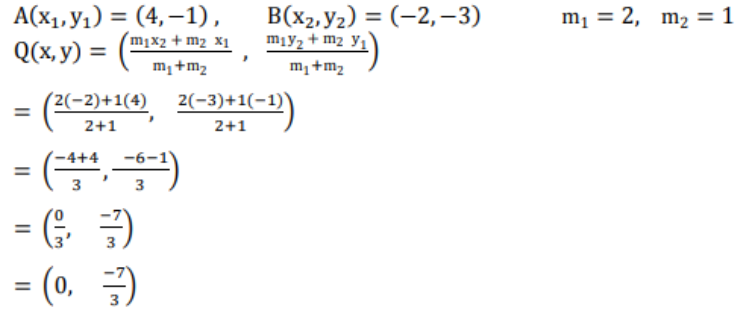
3) ಕ್ರೀಡಾದಿನದ ಚಟುವಟಿಕೆಗಳನ್ನು ನಡೆಸಲು, ಆಯತಾಕಾರದ ನಿಮ್ಮ ಶಾಲಾ ಮೈದಾನ ABCD ಯಲ್ಲಿ, 1m ಅಂತರದಲ್ಲಿ ಸೀಮೆಸುಣ್ಣದ ಪುಡಿಯಿಂದ ಗೆರೆಗಳನ್ನು ಎಳೆಯಲಾಗಿದೆ. AD ಯ ಉದ್ದಕ್ಕೂ ಪರಸ್ಪರ 1m ಅಂತರದಲ್ಲಿ 100 ಹೂವಿನ ಕುಂಡಗಳನ್ನು ಚಿತ್ರ 7.12 ರಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ಇರಿಸಲಾಗಿದೆ. ನಿಹಾರಿಕಾಳು AD ಯ 1/4 ರಷ್ಟು ದೂರವನ್ನು ಓಡಿ, 2ನೇ ಗೆರೆಯಲ್ಲಿ ಒಂದು ಹಸಿರು ಬಾವುಟವನ್ನು ನೆಡುತ್ತಾಳೆ. ಪ್ರೀತ್ AD ಯ 1/5 ರಷ್ಟು ದೂರವನ್ನು 8ನೇ ಗೆರೆಯಲ್ಲಿ ಓಡಿ, ಕೆಂಪು ಬಾವುಟವನ್ನು ನೆಡುತ್ತಾಳೆ. ಎರಡು ಬಾವುಟಗಳ ನಡುವಿನ ಅಂತರವೆಷ್ಟು? ರಶ್ಮಿಯು, ಈ ಇಬ್ಬರ ಬಾವುಟಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡದ ಮಧ್ಯದಲ್ಲಿ ನೀಲಿ ಬಾವುಟವನ್ನು ನೆಡಬೇಕೆಂದಾದರೆ, ಅವಳು ತನ್ನ ಬಾವುಟವನ್ನು ಎಲ್ಲಿ ನೆಡಬೇಕಾಗುತ್ತದೆ?
ಉತ್ತರ:
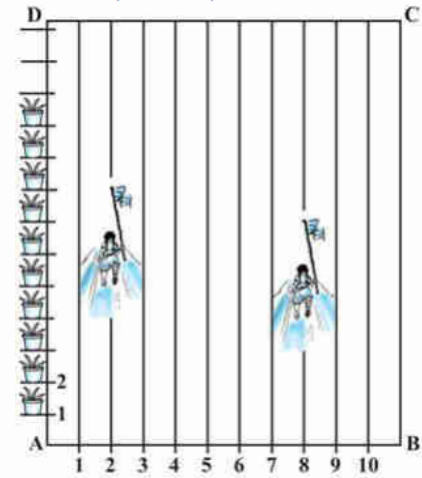

4) (-3, 10) ಮತ್ತು (6, -8) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವು (-1, 6) ರಿಂದ ಯಾವ ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸಲ್ಪಡುತ್ತದೆ ಎಂದು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

5) A (1, -5) ಮತ್ತು B (-4, 5) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವು X – ಅಕ್ಷದಿಂದ ಯಾವ ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸಲ್ಪಡುತ್ತದೆ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ವಿಭಾಗಿಸುವ ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕೂಡಾ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
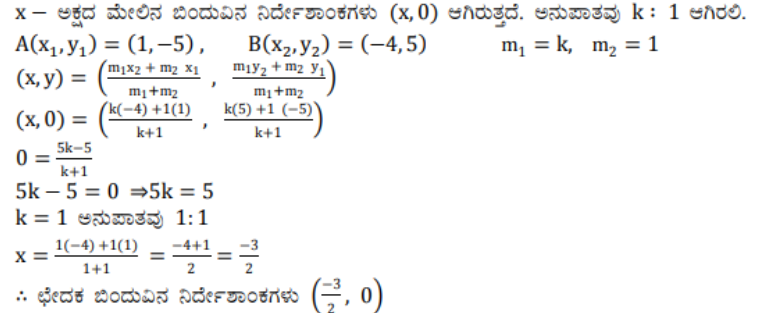
6) (1, 2), (4, y), (x, 6) ಮತ್ತು (3, 5) ಬಿಂದುಗಳು ಒಂದು ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಅನುಕ್ರಮ ಶೃಂಗಗಳಾದರೆ X ಮತ್ತು y ಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಬಿಂದುಗಳು
A(1, 2), B(4, y), C(x, 6) ಮತ್ತು D(3, 5)
ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಕರ್ಣಗಳು ಪರಸ್ಪರ ಒಂದನ್ನೊಂದು ಛೇದಿಸುತ್ತದೆ.
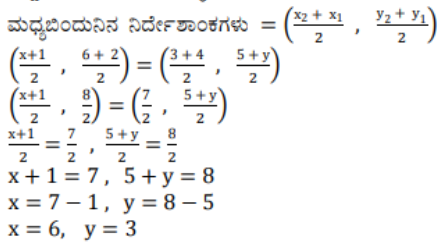
7) AB ವ್ಯಾಸವಾಗಿರುವ ವೃತ್ತದ ಕೇಂದ್ರ (2, -3) ಮತ್ತು B (1, 4) ಆದರೆ, A ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
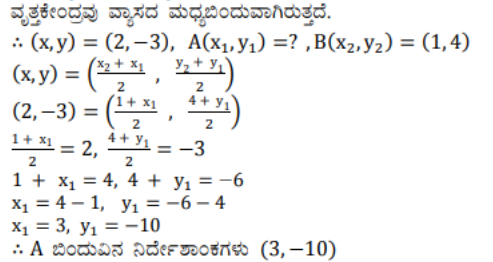
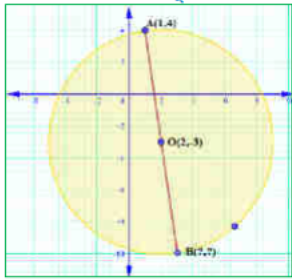
8) A ಮತ್ತು B ಗಳು ಕ್ರಮವಾಗಿ (-2, -2) ಮತ್ತು (2, -4) ಆಗಿದ್ದು AP = 3/7 AB ಆಗುವಂತೆ ರೇಖಾಖಂಡ AB ಯ ಮೇಲೆ ಇರುವ P ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

9) A (-2, 2) ಮತ್ತು B (2, 8) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವನ್ನು 4 ಸಮಭಾಗಗಳನ್ನಾಗಿ ಮಾಡುವ ಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:


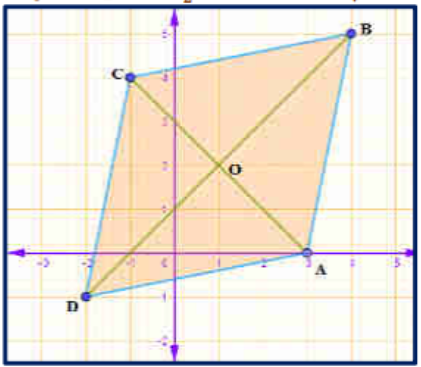
10) ಒಂದು ವಜಾಕೃತಿಯ ಅನುಕ್ರಮ ಶೃಂಗಗಳು (3, 0), (4, 5), (-1, 4) ಮತ್ತು (-2,-1) ಆದರೆ ಅದರ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. [ಸುಳುಹು: ವಜ್ರಾಕೃತಿಯ ವಿಸ್ತೀರ್ಣ = 1/2 (ಕರ್ಣಗಳ ಗುಣಲಬ್ಧ)]
ಉತ್ತರ:
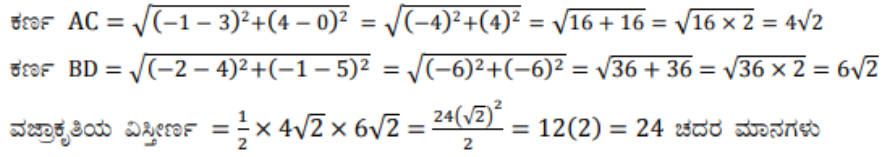
ಅಭ್ಯಾಸ 7.3
1) ಶೃಂಗಗಳು ಈ ಕೆಳಗಿನಂತಿರುವ ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
i) (2, 3), (-1, 0), (2, -4)
ii) (-5, -1), (3, -5) (5, 2)
ಉತ್ತರ:
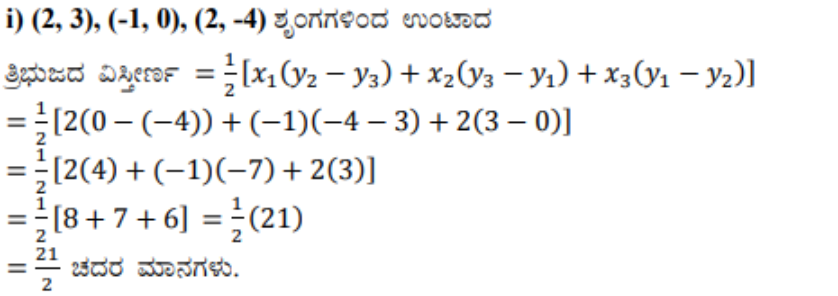
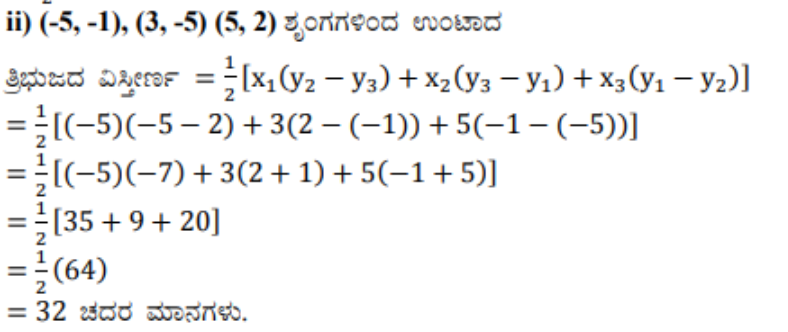
2) ಕೆಳಗಿನ ಪ್ರತಿಯೊಂದರಲ್ಲೂ, ಬಿಂದುಗಳು ಸರಳರೇಖಾಗತವಾಗಿದ್ದರೆ k ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
i) (7, -2), (5, 1), (3, k)
ii) (8, 1), (k, -4) (2, -5)
ಉತ್ತರ:
i) (7, -2), (5, 1), (3, k)
ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವು 0 ಆದರೆ ಕೊಟ್ಟಿರುವ ಮೂರು ಬಿಂದುಗಳು ಏಕರೇಖಾಗತವಾಗಿರುತ್ತದೆ.
A(7, -2), B(5, 1), ಮತ್ತು C (3, k)
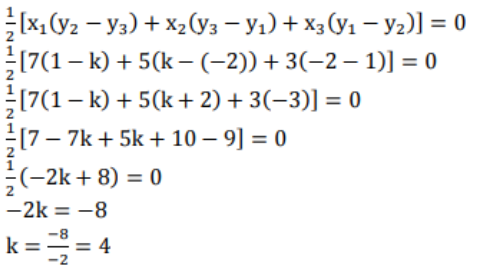
ii) (8, 1), (k, -4) (2, -5)
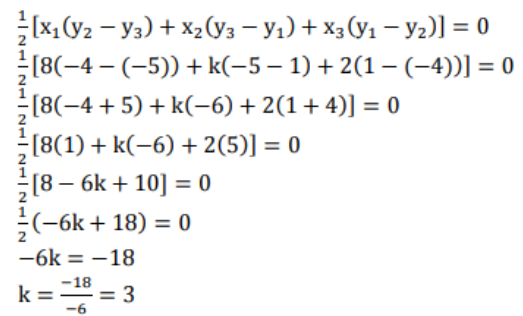
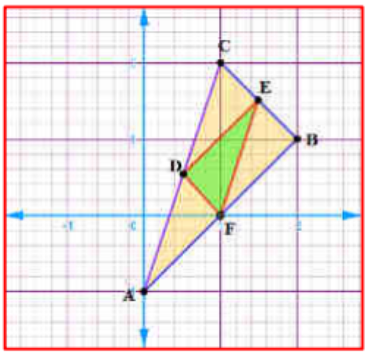
3) (0, -1), (2, 1) ಮತ್ತು (0, 3) ಶೃಂಗಬಿಂದುಗಳನ್ನು ಹೊಂದಿರುವ ತ್ರಿಭುಜದ ಬಾಹುಗಳ ಮಧ್ಯಬಿಂದುಗಳನ್ನು ಸೇರಿಸಿದಾಗ ಉಂಟಾಗುವ ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ಈ ತ್ರಿಭುಜ ಮತ್ತು ದತ್ತ ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
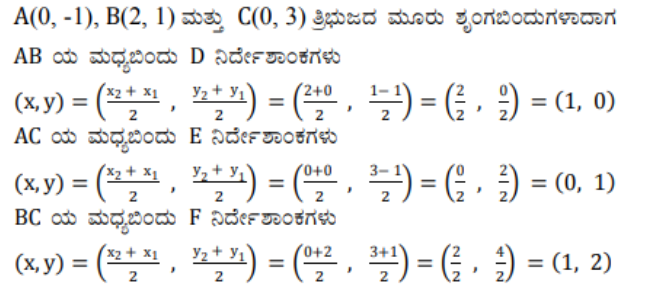

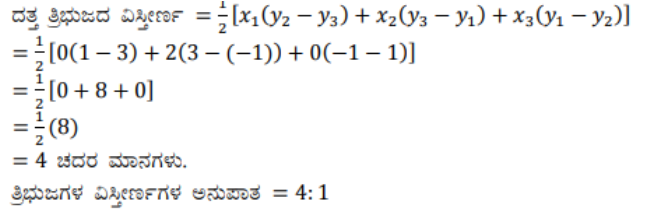
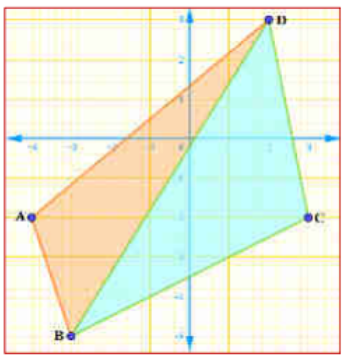
4) ಒಂದು ಚತುರ್ಭುಜದ ಅನುಕ್ರಮ ಶೃಂಗಗಳು (-4, -2), (-3, -5), (3, -2) ಮತ್ತು (2, 3) ಆದರೆ ಅದರ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

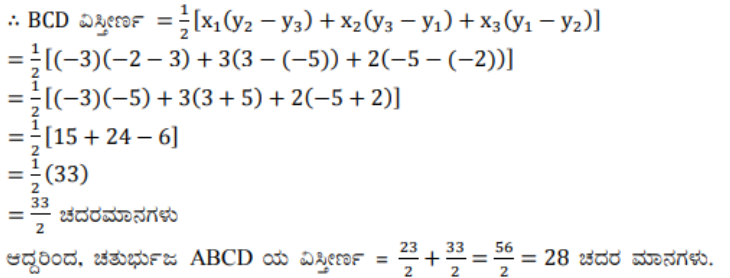
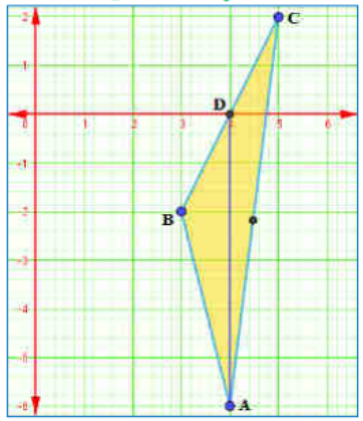
5) IX ತರಗತಿಯಲ್ಲಿ (ಅಧ್ಯಾಯ 9, ಉದಾಹರಣೆ 3) ಒಂದು ತ್ರಿಭುಜದ ಮಧ್ಯರೇಖೆಯು ಅದನ್ನು ಎರಡು ಸಮ ವಿಸ್ತೀರ್ಣದ ತ್ರಿಭುಜಗಳನ್ನಾಗಿ ವಿಭಾಗಿಸುತ್ತದೆಂದು ಕಲಿತಿದ್ದೀರಿ. ಇದನ್ನು A(4,-6), B (3, -2) ಮತ್ತು C (5, 2) ಶೃಂಗಬಿಂದುಗಳಾಗಿರುವ △ABC ಯಲ್ಲಿ ತಾಳೆ ನೋಡಿ.
ಉತ್ತರ:
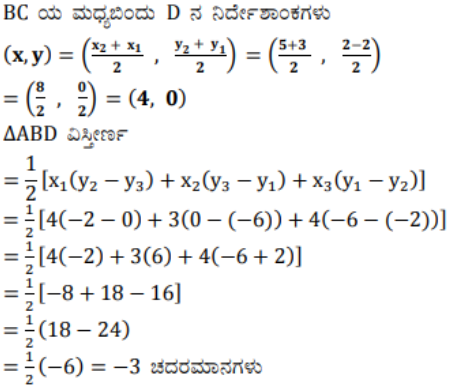
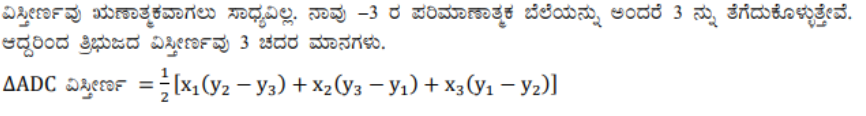

ಅಭ್ಯಾಸ 7.4 ( ಐಚ್ಛಿಕ)
1. 2x + y – 4 = 0 ಎಂಬ ರೇಖೆಯು A(2, – 2) B (3, 7) ಬಿಂದುಗಳಿಂದ ಉಂಟಾಗುವ ರೇಖಾಖಂಡವನ್ನು ವಿಭಾಗಿಸುವ ಅನುಪಾತವನ್ನು ನಿರ್ಧರಿಸಿ.
ಉತ್ತರ:
ಬೇಕಾದ ಅನುಪಾತ k : 1 ಮತ್ತು C ಬಿಂದುವು ಅನುಪಾತವನ್ನು ವಿಭಾಗಿಸುತ್ತದೆ.
∴ C ನಿರ್ದೇಶಾಂಕಗಳು
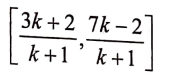
C ಬಿಂದುವು 2x + y = 4 = 0 ರೇಖೆಯ ಮೇಲೆ ಇರುವುದರಿಂದ
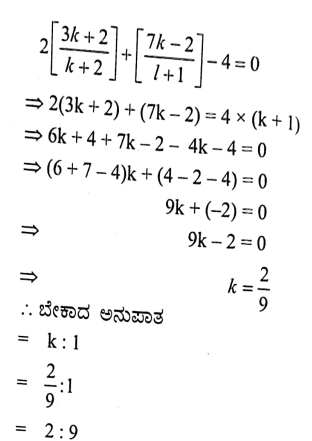
2. (x, y), (1.2) 2 (7, 0) ಬಿಂದುಗಳು ಸರಳರೇಖಾಗತವಾಗಿದ್ದರೆ, x ಮತ್ತು y ಗಳ ನಡುವೆ ಒಂದು ಸಂಬಂಧವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಬಿಂದುಗಳು
A(x, y) B(1, 2) 2 C(7,0)
A, B ಮತ್ತು Cಗಳು ಸರಳರೇಖಾಗತವಾದರೆ
x(2 + 0) + 1(0 – y) + 7(y – 2) = 0
2 x – y + 7y – 14 = 0
2x + 6y – 14 = 0
x + 3y – 7 = 0
x ಮತ್ತು y ಗಳ ನಡುವೆ ಬೇಕಾದ ಸಂಬಂಧ x + 3y – 7 = 0
3. (6, -6), (3, -7) ಮತ್ತು (3, 3) 2 ಎಂಬ ಬಿಂದುಗಳ ಮೂಲಕ ಹಾದುಹೋಗುವ ವೃತ್ತದ ಕೇಂದ್ರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
p(x, y) ವೃತ್ತದ ಕೇಂದ್ರ ಬಿಂದು
A(6, – 6) B(3, – 7) 2 C(3,3)
∴ AP = BP = CP
AP = BP ಯನ್ನು ತೆಗೆದೆಕೊಂಡಾಗ AP2 = BP2
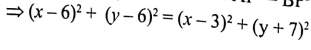

4. ಒಂದು ಚೌಕದ ಎರಡು ಅಭಿಮುಖ ಅಭಿಮುಖ ಶೃಂಗಗಳ ನಿರ್ದೇಶಾಂಕಗಳು (-1, 2) (3, 2) ಆಗಿವೆ. ಉಳಿದೆರಡು ಶೃಂಗಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
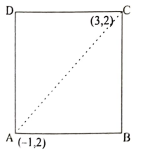
ಚೌಕ ABCD ಯ ಶೃಂಗ ಬಿಂದುಗಳು
A(- 1, 2) ಮತ್ತು C(3,2)
B(x, y) ಗೊತ್ತಿರದ ಶೃಂಗ ಬಿಂದು.
ಚೌಕದ ನಾಲ್ಕು ಪಾರ್ಶ್ವಗಳು ಸಮನಾಗಿರುವುದರಿಂದ

5. ಕೃಷ್ಣನಗರದ ಮಾಧ್ಯಮಿಕ ಶಾಲೆಯೊಂದರ X ತರಗತಿಯ ವಿದ್ಯಾರ್ಥಿಗಳಿಗೆ ಹೊದೋಟವನ್ನು ನಿರ್ಮಿಸುವ ಚಟುವಟಿಕೆಗಾಗಿ ಆಯತಾಕಾರದ ಜಮೀನನು ನೀಡಲಾಗಿದೆ. ಜಮೀನಿನ ಸೀಮಾರೇಖೆಯಲ್ಲಿ ಗುಲ್ಮೊಹರ್ನ ಸಸಿಗಳನ್ನು Im ಅಂತರದಲ್ಲಿ ನೆಡಲಾಗಿದೆ. ಜಮೀನಿನ ಒಳಭಾಗದಲ್ಲಿ ಚಿತ್ರ 7.14 ರಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ, ತ್ರಿಭುಜಾಕಾರದ ಒಂದು ಹುಲ್ಲು ಹಾಸು ಇದೆ. ಜಮೀನಿನ ಉಳಿದ ಭಾಗದಲ್ಲಿ ವಿದ್ಯಾರ್ಥಿಗಳು ಹೂ ಗಿಡಗಳ ಬೀಜಗಳನ್ನು ಬಿತ್ತಬೇಕಾಗಿದೆ.
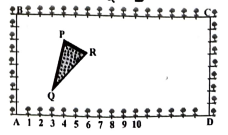
i) A ಯನ್ನು ಮೂಲಬಿಂದುವೆಂದು ಪರಿಗಣಿಸಿ, ತ್ರಿಭುಜದ ಶೃಂಗಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ii) C ಯು ಮೂಲಬಿಂದುವೆಂದು ∆PQR ನ ಶೃಂಗಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ಈ ಪ್ರಕರಣದಲ್ಲಿ, ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ನೀವು ಏನನ್ನು ಗಮನಿಸಿದಿರಿ?
ಉತ್ತರ:
(i) A ಯನ್ನು ಮೂಲ ಬಿಂದು ಆಗಿರಿಸಿ AD ಮತ್ತು AB ಅಕ್ಷಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ P( 4 , 6) Q(3, 2) ಮತ್ತು R (6, 5) ∆PQR 2 ಶೃಂಗಬಿಂದುಗಳು.
(ii) C ಯನ್ನು ಮೂಲ ಬಿಂದು ಆಗಿರಿಸಿ CB ಮತ್ತು CD ಅಕ್ಷಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ ∆PQD ನ ಶೃಂಗಬಿಂದುಗಳು.
P(12,2) Q(13, 6) ಮತ್ತು R(10, 3) APQR ನ ವಿಸ್ತೀರ್ಣ
P(4,6) Q(3, 2) ಮತ್ತು R(6, 5) ಶೃಂಗಬಿಂದುಗಳು ಆದಾಗ
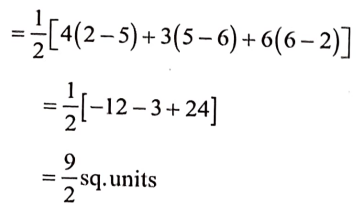
∆PQR ನ ವಿಸ್ತೀರ್ಣ ಎರಡು ಪ್ರಕರಣಗಳಲ್ಲೂ ಸಮ.

∆ABC ಯ ವಿಸ್ತೀರ್ಣದೊಂದಿಗೆ ಹೋಲಿಸಿರಿ. (ಪ್ರಮೇಯ 6.2 ಮತ್ತು ಪ್ರಮೇಯ 6.6 ನ್ನು ನೆನಪಿಸಿಕೊಳ್ಳಿ
ಉತ್ತರ:

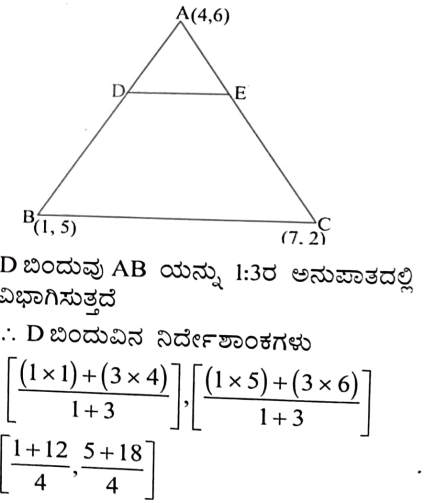

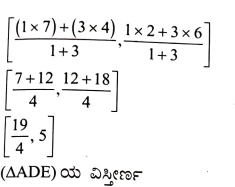
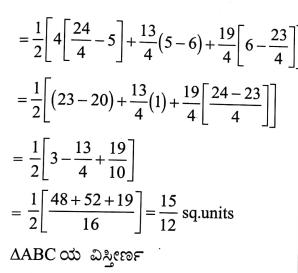
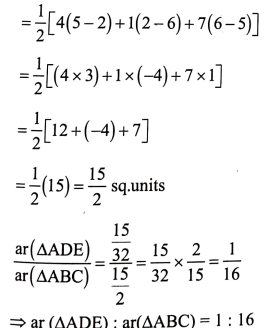
7. A (4, 2), B (6.5) ಮತ್ತು C (1.4) ಇವುಗಳು ∆ABC ಯ ಶೃಂಗಬಿಂದುಗಳಾಗಿರಲಿ.
i) A ಯಿಂದ ಎಳೆದ ಮಧ್ಯರೇಖೆಯು BC ಯನ್ನು D ಯಲ್ಲಿ ಸಂಧಿಸುತ್ತದೆ. D ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ii) AP: PD = 2: 1 ಆಗುವಂತೆ. AD ಯ ಮೇಲೆ ಇರುವ P ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
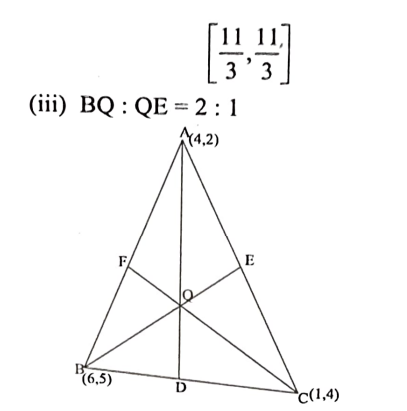
iii) BQ : QE = 2 : 1 ಮತ್ತು CR : RF = 2 : 1 ಆಗುವಂತೆ, BE ಮತ್ತು CF ಮಧ್ಯರೇಖೆಗಳ ಮೇಲೆ ಕ್ರಮವಾಗಿ ಇರುವ Q ಮತ್ತು R ಬಿಂದುಗಳ ಕಂಡುಹಿಡಿಯಿರಿ.
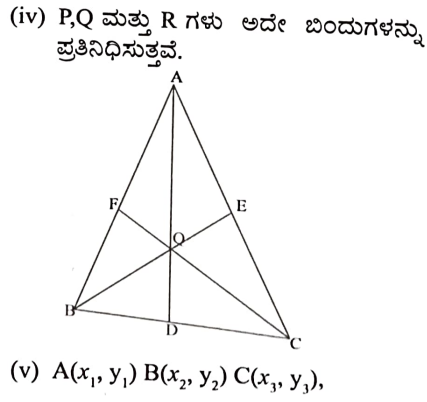
iv) ನೀವು ಏನನ್ನು ಗಮನಿಸಿದಿರಿ?
[ಸೂಚನೆ: ಎಲ್ಲಾ ಮೂರು ಮಧ್ವರೇಖೆಗಳಿಗೂ ಸಾಮಾನ್ಯವಾಗಿರುವ ಬಿಂದುವನ್ನು ‘ಗುರುತ್ವಕೇಂದ್ರ’ ಎನ್ನುತ್ತೇವೆ. ಇದು ಪ್ರತಿಯೊಂದು ಮಧ್ಯರೇಖೆಯನ್ನು 2 : 1 ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುತ್ತದೆ.]
v) A(x1, y1,), B(x2, y2) C (x3,y3) ಗಳು ∆ABC ಯ ಶೃಂಗಬಿಂದುಗಳಾದರೆ ತ್ರಿಭುಜದ ಗುರುತ್ವಕೇಂದ್ರದ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

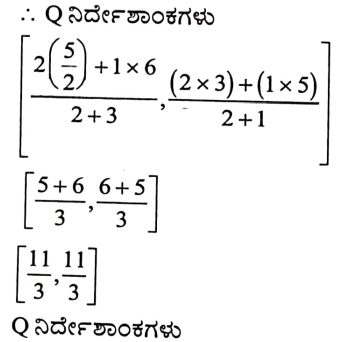

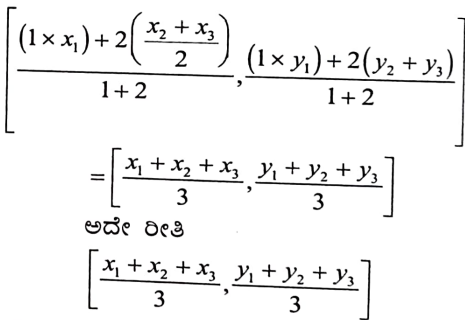
∆ABCD A (-1, 1), B(-1, 4), C (5, 4) 2 D (5, -1) ಬಿಂದುಗಳಿಂದ ಉಂಟಾದ ಒಂದು ಆಯತ. P, Q, R ಮತ್ತು S ಗಳು ಕ್ರಮವಾಗಿ, AB, BC, CD ಮತ್ತು DA ಗಳ ಮಧ್ಯಬಿಂದುಗಳು. ಚತುರ್ಭುಜ ABCD ಯು ಒಂದು ವರ್ಗವೆ? ಒಂದು ಆಯತವೇ? ಅಥವಾ, ಒಂದು ವಜ್ರಾಕೃತಿಯೇ? ನಿಮ್ಮ ಉತ್ತರವನ್ನು ಸಮರ್ಥಿಸಿ.
ಉತ್ತರ:

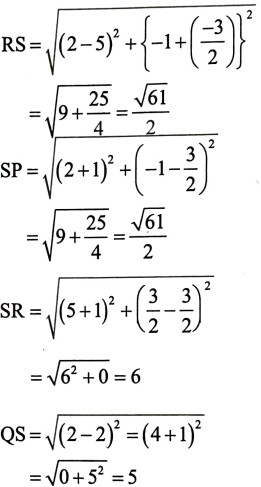
ನಾವು ಗಮನಿಸಿದಂತೆ PQ = QR = RS =SP PQRS ನ ಎಲ್ಲಾ ಬಾಹುಗಳು ಸಮವಾಗಿವೆ ಆದ್ದದಿಂದ ಇದು ವಜ್ರಾಕೃತಿ.
ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು


ಇತರೆ ವಿಷಯಗಳು :
10ನೇ ತರಗತಿ ಗಣಿತ ರಚನೆಗಳು ನೋಟ್ಸ್
10ನೇ ತರಗತಿ ಗಣಿತ ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ನೋಟ್ಸ್
