10th Standard Vastava Sankhyegalu Maths Notes Question Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, 10ನೇ ತರಗತಿ ಗಣಿತ ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು, 10th Standard Maths Notes Pdf, 10th Standard Maths Notes Part – 1, vastava sankhyegalu in kannada notes, ganitha notes kannada, ಗಣಿತ ನೋಟ್ಸ್ 10ನೇ ತರಗತಿ pdf, class 10th maths chapter 8 notes in kannada medium, kseeb solutions for class 10 maths chapter 8 notes pdf, 10ನೇ ತರಗತಿ ಗಣಿತ ನೋಟ್ಸ್, sslc vastava sankegalu in kannada.
ಘಟಕ 08 – ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು
ಅಭ್ಯಾಸ 8.1
1. ಯೂಕ್ಲಿಡ್ನ ಭಾಗಾಕಾರ ಕ್ರಮವಿಧಿಯನ್ನು ಉಪಯೋಗಿಸಿ ಈ ಕೆಳಗಿನ ಸಂಖ್ಯೆಗಳ ಮ.ಸಾ.ಅ. ವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) 135 ಮತ್ತು 225
(ii) 196 ಮತ್ತು 38220
(iii) 867 ಮತ್ತು 255
(i) 135 ಮತ್ತು 225
ಉತ್ತರ:

(ii) 196 ಮತ್ತು 38220
ಉತ್ತರ:

(iii) 867 ಮತ್ತು 255
ಉತ್ತರ:

2. ಯಾವುದೇ ಧನ ಬೆಸ ಪೂರ್ಣಾಂಕವು 6q+1 ಅಥವಾ 6q+3 ಅಥವಾ 6q+5 ರೂಪದಲ್ಲಿರುತ್ತದೆ ಎಂದು ತೋರಿಸಿ. ಇಲ್ಲಿ q ಒಂದು ಪೂರ್ಣಾಂಕವಾಗಿದೆ.
ಉತ್ತರ:
a ಯು ಒಂದು ಧನ ಬೆಸ ಸಂಖ್ಯೆ ಆಗಿರಲಿ. b = 6 ಆಗಿರಲಿ
ಆದ್ದರಿಂದ ಯೂಕ್ಲಿಡ್ ಭಾಗಾಕಾರ ಅಲ್ಗಾರಿಥಂ ಪ್ರಕಾರ,
a = bq + r[0 <= r < b]
a = 6q + r[r = 0, 1, 2, 3, 4, 5]
(i) r = 0 ಆದಾಗ, a =6q → ಇದು 2ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ 6q ಒಂದು ಸಮ ಸಂಖ್ಯೆ
(ii) r = 1 ಆದಾಗ, a = 6q + 1 → ಇದು 2ರಿಂದ ಭಾಗವಾಗುವುದಿಲ್ಲ. ಆದ್ದರಿಂದ 6q + 1 ಒಂದು ಬೆಸ ಸಂಖ್ಯೆ.
(iii) r = 2 ಆದಾಗ, a = 6q + 2 → ಇದು 2ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ 6q + 2ಒಂದು ಸಮ ಸಂಖ್ಯೆ.
(iv) r = 3 ಆದಾಗ, a = 6q + 3 → ಇದು 2ರಿಂದ ಭಾಗವಾಗುವುದಿಲ್ಲ. ಆದ್ದರಿಂದ 6q + 3 ಒಂದು ಬೆಸ ಸಂಖ್ಯೆ.
(v) r = 4 ಆದಾಗ, a = 6q + 4 → ಇದು 2ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ 6q + 4ಒಂದು ಸಮ ಸಂಖ್ಯೆ.
(iv) r = 5 ಆದಾಗ, a = 6q + 5 → ಇದು 2ರಿಂದ ಭಾಗವಾಗುವುದಿಲ್ಲ. ಆದ್ದರಿಂದ 6q + 5 ಒಂದು ಬೆಸ ಸಂಖ್ಯೆ
ಆದ್ದರಿಂದ ಯಾವುದೇ ಧನ ಬೆಸ ಪೂರ್ಣಾಂಕವು 6q + 1 ಅಥವಾ 6q + 3 ಅಥವಾ 6q + 5 ರೂಪದಲ್ಲಿರುತ್ತದೆ.
3. 32 ಸದಸ್ಯರುಳ್ಳ ಭೂದಳದ ತುಕಡಿಯ ಹಿಂದೆ 616 ಸದಸ್ಯರುಳ್ಳ ಭೂದಳ ಸೈನಿಕರ ಗುಂಪು ಒಂದು ಪಥ ಸಂಚಲನದಲ್ಲಿ ಚಲಿಸಬೇಕಾಗಿದೆ. ಆ ಎರಡೂ ತಂಡಗಳು ಒಂದೇ ಸಂಖ್ಯೆಯ ಕಂಬಸಾಲುಗಳಲ್ಲಿ ಚಲಿಸಬೇಕಾಗಿದೆ. ಗರಿಷ್ಠ ಎಷ್ಟು ಕಂಬಸಾಲುಗಳಲ್ಲಿ ಅವರು ಈ ರೀತಿ ಚಲಿಸಬಹುದು?
ಉತ್ತರ:
32 ಸದಸ್ಯರುಳ್ಳ ಭೂದಳದ ತುಕಡಿಯ ಹಿಂದೆ 616 ಸದಸ್ಯರುಳ್ಳ ಭೂದಳ ಸೈನಿಕರ ಗುಂಪು ಒಂದು ಪಥ ಸಂಚಲನದಲ್ಲಿ ಚಲಿಸಬೇಕಾಗಿದೆ. 616 >32, ಆಗಿರುವುದರಿಂದ ಯೂಕ್ಲಿಡ್ನ ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯವನ್ನು ಅನ್ವಯಿಸಿದಾಗ
616 = (32 x19) + 8
ಈಗ, ಭಾಜಕ 8 ಮತ್ತು ಭಾಗಲಬ್ಧ 32
32 = 8 x 4 = 0
ಶೇಷವು 0 ಆಗಿರುವುದರಿಂದ
ಮ.ಸಾ.ಅ (616, 32) = 8
ಎರಡು ತಂಡಗಳು ಚಲಿಸಬಹುದಾದ ಗರಿಷ್ಥ ಕಂಬಸಾಲುಗಳು = 8.
4. ಯೂಕ್ಲಿಡ್ನ ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯವನ್ನು ಬಳಸಿ. ಯಾವುದೇ ಧನ ಪೂರ್ಣಾಂಕದ ವರ್ಗವು 3m ಅಥವಾ 3m+1 ರೂಪದಲ್ಲಿಯೇ ಇರುತ್ತದೆ ಎಂದು ತೋರಿಸಿ. ತೋರಿಸಿ. ಇಲ್ಲಿ m ಒಂದು ಪೂರ್ಣಾಂಕ
[ಸುಳುಹು: X ಎಂಬುದು ಯಾವುದೇ ಧನ ಪೂರ್ಣಾಂಕ ಆಗಿರಲಿ. ಆಗ ಅದು 3q. 3q+1 ಅಥವಾ 3q+2 ರೂಪದಲ್ಲಿರುತ್ತದೆ. ಈಗ ಪ್ರತಿಯೊಂದನ್ನೂ ವರ್ಗಗೊಳಿಸಿ ಮತ್ತು ಅವುಗಳನ್ನು 3m ಅಥವಾ 3m + 1 ರೂಪದಲ್ಲಿ ಪುನಃ ಬರೆಯಬಹುದು ಎಂದು ತೋರಿಸಿ.]
ಉತ್ತರ:

5. ಯೂಕ್ಲಿಡ್ನ ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯವನ್ನು ಉಪಯೋಗಿಸಿ ಯಾವುದೇ ಧನ ಪೂರ್ಣಾಂಕದ ಘನವು 9m, 9m+1 ಅಥವಾ 9m+8 ರೂಪದಲ್ಲಿರುತ್ತದೆ ಎಂದು ತೋರಿಸಿ.
ಉತ್ತರ:
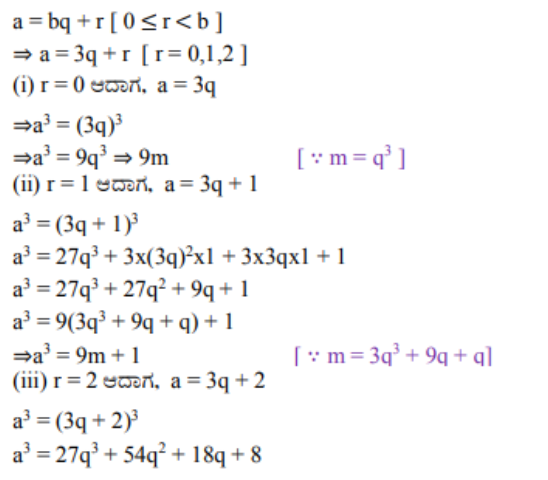
ಅಭ್ಯಾಸ 8.2
1. ಕೆಳಗಿನ ಪ್ರತಿ ಸಂಖ್ಯೆಯನ್ನು ಅದರ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳ ಗುಣಲಬ್ಧವಾಗಿ ವ್ಯಕ್ತಪಡಿಸಿ.
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
ಉತ್ತರ:
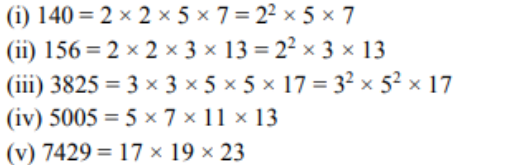
2. ಕೆಳಗೆ ನೀಡಿರುವ ಜೋಡಿ ಪೂರ್ಣಾಂಕಗಳ ಲ.ಸಾ.ಅ. ಮತ್ತು ಮ.ಸಾ.ಅ. ಗಳನ್ನು ಕಂಡುಹಿಡಿದು. ಲ.ಸಾ.ಅ. X ಮ.ಸಾ.ಅ. = ಆ ಎರಡು ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧ ಎಂಬುದನ್ನು ತಾಳೆ ನೋಡಿ.
(i) 26 ಮತ್ತು 91
(ii) 510 ಮತ್ತು 92
(iii) 336 ಮತ್ತು 54
ಉತ್ತರ:
(i) 26 ಮತ್ತು 91
26 = 2 x 13
91 = 13 x 7
ಮ.ಸಾ.ಅ (26, 91) = 13
ಲ.ಸಾ.ಅ (26, 91) = 13 x 2 x 7 = 182
ತಾಳೆ: ಲ.ಸಾ.ಅ x ಮ.ಸಾ.ಅ
= 182 x 13 = 2366
AxB = ಎರಡು ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧ 26 x 91 = 2366
ಆದ್ದರಿಂದ ಲ.ಸಾ.ಅ x ಮ.ಸಾ.ಅ = ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧ
(ii) 510 ಮತ್ತು 92
510 = 2 x 3 x 5 x 17
92 = 2 x 2 x 23
ಮ.ಸಾ.ಅ = 2
ಲ.ಸಾ.ಅ = 2 x 2 x 3 x 5 x 17 x 23 = 23460
ಮ.ಸಾ.ಅ x ಲ.ಸಾ.ಅ = 2 x 23460 = 46920
510 ಮತ್ತು 92 ರ ಗುಣಲಬ್ಧ
510 x 93 = 46920
ಆದ್ದರಿಂದ ಲ.ಸಾ.ಅ x ಮ.ಸಾ.ಅ =ಎರಡು ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧ
(iii) 336 ಮತ್ತು 54
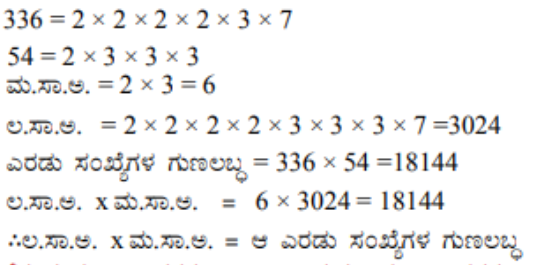
3. ಕೆಳಗಿನ ಪೂರ್ಣಾಂಕಗಳ ಲ.ಸಾ.ಅ ಮತ್ತು ಮ.ಸಾ.ಅ.ಗಳನ್ನು ಅವಿಭಾಜ್ಯ ಅಪವರ್ತ ವಿಧಾನದಿಂದ ಕಂಡುಹಿಡಿಯಿರಿ.
(1) 12,15 ಮತ್ತು 21 (ii) 17,23 ಮತ್ತು 29 (iii) 8,9 ಮತ್ತು 25.
(1) 12,15 ಮತ್ತು 21
12 x 2 x 2 x 3
15 = 3 x 5
21 = 3 x 7
ಮ.ಸಾ.ಅ (12, 15, 21) = 3
ಲ.ಸಾ.ಅ (12, 15, 21) = 3 x 22 x 5 x 1 =420
(ii) 17,23 ಮತ್ತು 29
17 = 17 x 1
23 = 23 x 1
29 = 29 x1
ಮ.ಸಾ.ಅ (17, 23, 29) = 1
ಲ.ಸಾ.ಅ (17, 23, 29) = 17 x 23 x 29 = 11339
ಆದ್ದರಿಂದ H x L = A x B
(iii) 8,9 ಮತ್ತು 25.
8 = 23 x 1
9 = 32 x 1
25 = 52 x 1
ಮ.ಸಾ.ಅ (8, 9, 25) = 1
ಲ.ಸಾ.ಅ (8,9,25)= 23 x 32 52 = 1800
ಆದ್ದರಿಂದ H x L = A x B
4. (306, 657) ರ ಮ.ಸಾ.ಅ = 9 ಆದರೆ ಅವುಗಳ ಲ.ಸಾ.ಅ.ವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
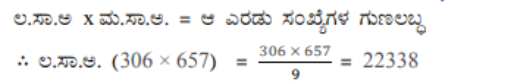
5. n ದ ಯಾವುದೇ ಬೆಲೆಗೆ 6n ಇದು ಸೊನ್ನೆಯಿಂದ ಕೊನೆಗೊಳ್ಳಬಹುದೇ? ಪರೀಕ್ಷಿಸಿ. ಇಲ್ಲಿ n ಒಂದು ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಯಾಗಿದೆ..
ಉತ್ತರ:
n ∈ N ಬೆಲೆಯು 6° ಇದು ಸೊನ್ನೆಯಿಂದ ಕೊನೆಗೊಳ್ಳಬೇಕಾದರೆ, ಅದು 5 ರಿಂದ ನಿಶ್ಯೇಷವಾಗಿ ಭಾಗಿಸಲ್ಪಡಬೇಕು ಅಂದರೆ, 6n ಇದರ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತಿಸುವಿಕೆಯು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ 5ನ್ನು ಒಳಗೊಂಡಿರಬೇಕು.
6. 7 × 11 × 13 + 13 ಮತ್ತು 7 × 6 × 5 × 4 × 3 × 2 ×1 + 5 ಇವು ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಗಳಾಗಿವೆ ಏಕೆ? ವಿವರಿಸಿ.
ಉತ್ತರ:
(7 x 11 x 13) + 13
= 13{(7 x 11) + 1} = 13(77 + 1)
= 13 x 78 ( ∴ 78-13×6)
= 13 X 13 X 6 = 132 X 2 X 3
ಸಂಯುಕ್ತ ಸಂಖ್ಯೆ ಆಗಬೇಕಾದರೆ
(7 x 6 x 5 x 4 x 3 x 2 x 1) + 5
= 5 {(7 x 6 x 4 x 3 x 2 x 1) + 1}
5(1008 + 1) = 5 * 1009 ಒಂದು ಸಂಯುಕ್ತ ಸಂಖ್ಯೆ
7. ಒಂದು ಕ್ರೀಡಾಂಗಣದ ಸುತ್ತಲೂ ವೃತ್ತಾಕಾರದ ಮಾರ್ಗವಿದೆ. ಸೋನಿಯಾಳು ಆ ಕ್ರೀಡಾಂಗಣದ ಒಂದು ಸುತ್ತನ್ನು ಪೂರ್ಣಗೊಳಿಸಲು 18 ನಿಮಿಷಗಳನ್ನು ತೆಗೆದುಕೊಂಡರೆ, ರವಿಯು ಅದೇ ಸುತ್ತನ್ನು ಪೂರ್ಣಗೊಳಿಸಲು 12 ನಿಮಿಷಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತಾನೆ. ಒಂದೊಮ್ಮೆ ಅವರಿಬ್ಬರೂ ಒಂದೇ ಬಿಂದುವಿನಿಂದ ಏಕಕಾಲದಲ್ಲಿ ಆರಂಭಿಸಿ, ಏಕಮುಖವಾಗಿ ಚಲಿಸಿದರೆ, ಎಷ್ಟು ನಿಮಿಷಗಳ ನಂತರ ಅವರು ಪುನಃ ಆರಂಭಿಕ ಬಿಂದುವಿನಲ್ಲಿ ಸಂಧಿಸುತ್ತಾರೆ?
ಉತ್ತರ:
18 ಮತ್ತು 12 ರ ಲ.ಸಾ.ಅ
18 = 2 x 3 x 3
12 = 2 x 2 x 3
ಲ.ಸಾ.ಅ = 2 2 x 32 = 36
36 ನಿಮಿಷಗಳಲ್ಲಿ ಸೊನಿಯಾಳು ಆ ಕ್ರೀಡಾಂಗಣದ 2 ಸುತ್ತನ್ನು ಸುತ್ತುತ್ತಾಳೆ 36 ನಿಮಿಷಗಳಲ್ಲಿ ರವಿಯು ಆ ಕ್ರೀಡಾಂಗಣದ 3 ಸುತ್ತನ್ನು ಸುತ್ತುತ್ತಾನೆ.
36 ನಿಮಿಷಗಳ ನಂತರ ಅವರು ಪುನಃ ಆರಂಭಿಕ ಬಿಂದುವಿನಲ್ಲಿ ಸಂಧಿಸುತ್ತಾರೆ.
ಅಭ್ಯಾಸ 8.3
1. √5 ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

2. 3 + 2√5 ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

3. ಈ ಕೆಳಗಿನ ಸಂಖ್ಯೆಗಳು ಅಭಾಗಲಬ್ಧಗಳೆಂದು ಸಾಧಿಸಿ.
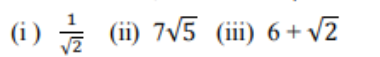
ಉತ್ತರ:

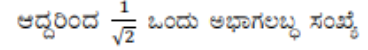


ಅಭ್ಯಾಸ 8.4
1. ದೀರ್ಘ ಭಾಗಾಕಾರ ಕ್ರಿಯೆಯನ್ನು ಮಾಡದೇ, ಈ ಕೆಳಗಿನ ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು ಅಂತ್ಯಗೊಳ್ಳುವ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯನ್ನು ಹೊಂದಿವೆಯೇ ಅಥವಾ ಅಂತ್ಯಗೊಳ್ಳದೇ ಆವರ್ತವಾಗುವ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯನ್ನು ಹೊಂದಿವೆಯೇ ತಿಳಿಸಿ:
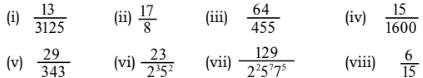

ಉತ್ತರ:

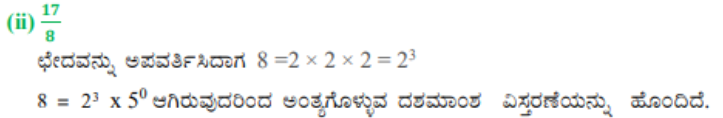

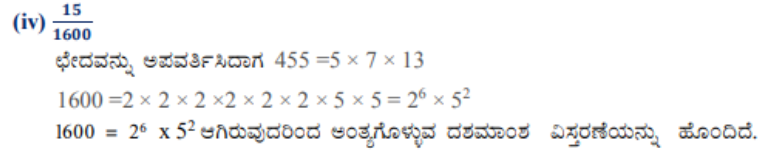



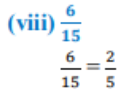



2. ಪ್ರಶ್ನೆ 1ರಲ್ಲಿನ ಅಂತ್ಯಗೊಳ್ಳುವ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯನ್ನು ಹೊಂದಿರುವ ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಗಳನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
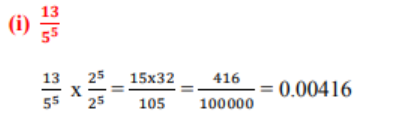
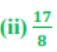
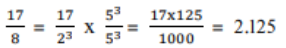
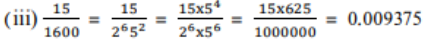
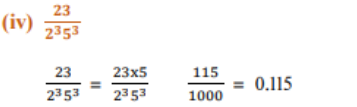
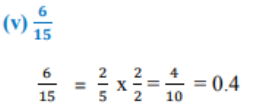
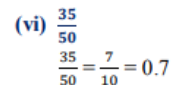
3. ಕೆಲವು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯನ್ನು ಈ ಕೆಳಗೆ ನೀಡಿದೆ. ಆ ಪ್ರತಿಯೊಂದು ಸಂಖ್ಯೆಯೂ ಭಾಗಲಬ್ಧವೇ ಅಥವಾ ಅಲ್ಲವೇ ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸಿ. ಅವು ಭಾಗಲಬ್ಧ P ಸಂಖ್ಯೆಗಳಾಗಿದ್ದು, p/q ರೂಪದಲ್ಲಿದ್ದರೆ, q ದ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳ ಬಗ್ಗೆ ನೀವು ಏನನ್ನು ಹೇಳುವಿರಿ?
(i) 43.123456789
(ii) 0.120120012000120000…
(iii) 43.123456789
ಉತ್ತರ:
(i) 43.123456789
43.123456789 – ದು ಅಂತ್ಯಗೊಳ್ಳುವ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯನ್ನು ಹೊಂದಿದೆ.
ಆದ್ದರಿಂದ ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯಾಗಿದ್ದು p/q ರೂಪದಲ್ಲಿದೆ.
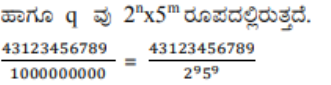
(ii) 0.120120012000120000…
ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯು ಪುನರಾವರ್ತಿತವಾದರೂ ಕೊನೆಗೊಳ್ಳುವುದಿಲ್ಲ. ಆದ್ದರಿಂದ ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯೆಯು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ

ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. (ಯೂಕ್ಲಿಡ್ ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯ): ದತ್ತ ಧನ ಪೂರ್ಣಾಂಕಗಳಾದ a ಮತ್ತು b ಗಳಿಗೆ, a = bq + r ಗೆ ಸರಿಹೊಂದುವಂತೆ q ಮತ್ತು r ಎಂಬ ಎರಡು ಅನನ್ಯ ಪೂರ್ಣಾಂಕಗಳಿರುತ್ತವೆ ಮತ್ತು ಇಲ್ಲಿ0 < c =<b ಆಗಿರುತ್ತದೆ. a + by
2. ಕ್ರಮವಿಧಿ ಎಂಬುದು, ಒಂದು ಸಮಸ್ಯೆಯನ್ನು ಬಿಡಿಸುವ ವಿಧಾನವನ್ನು ತಿಳಿಸುವ, ಸ್ಪಷ್ಟವಾಗಿ ನಿರೂಪಿಸಲ್ಪಟ್ಟ ವಿವಿಧ ಹಂತಗಳ ಸರಣಿಯಾಗಿದೆ.
3. ಅಂಕಗಣಿತದ ಮೂಲ ಪ್ರಮೇಯವು ಧನ ಪೂರ್ಣಾಂಕಗಳ ಗುಣಾಕಾರಕ್ಕೆ ಸಂಬಂಧಿಸಿದೆ.
4. ಯೂಕ್ಲಿಡ್ನ ಭಾಗಾಕಾರ ಕ್ರಮವಿಧಿಯನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ನಿರೂಪಿಸೋಣ. c > d ಆಗಿರುವಂತಹ c ಮತ್ತು d ಎಂಬ ಎರಡು ಧನ ಪೂರ್ಣಾಂಕಗಳ ಮ.ಸಾ.ಅ.ವನ್ನು ಕಂಡುಹಿಡಿಯಲು ನಾವು ಕೆಳಗಿನ ಹಂತಗಳು ಅನುಸರಿಸುತ್ತೇವೆ.
ಹಂತ 1: ಯೂಕ್ಲಿಡ್ ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯವನ್ನು c ಮತ್ತು d ಗಳಿಗೆ ಅನ್ವಯಿಸಿದಾಗ, c = dq + r ಆಗುವಂತೆ q ಮತ್ತು r ಎಂಬ ಎರಡು ಪೂರ್ಣ ಸಂಖ್ಯೆಗಳನ್ನು ನಾವು ಪಡೆಯುತ್ತೇವೆ. ಇಲ್ಲಿ 0 < r < d ಆಗಿರುತ್ತದೆ.
ಹಂತ 2: r = 0 ಆದರೆ, d ಯು c ಮತ್ತು d ಗಳ ಮ.ಸಾ.ಅ. ಆಗಿರುತ್ತದೆ. r ≠ 0 ಆದರೆ, ಭಾಗಾಕಾರ ಅನುಪ್ರಮೇಯವನ್ನು d ಮತ್ತು r ಗಳಿಗೆ ಅನ್ವಯಿಸಿ.
ಹಂತ 3: ಶೇಷವು ಸೊನ್ನೆಯಾಗುವತನಕ ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಮುಂದುವರಿಸಿ. ಈ ಹಂತ (ಶೂನ್ಯ ಶೇಷ) ದಲ್ಲಿನ ಭಾಜಕವು ಅಪೇಕ್ಷಿತ ಮ.ಸಾ.ಅ. ಆಗಿರುತ್ತದೆ.
ಇಲ್ಲಿ ಮ.ಸಾ.ಅ (c, d) = ಮ.ಸಾ.ಅ. (d,r) ಆಗಿರುವುದರಿಂದ. ಈ ಕ್ರಮವಿಧಿಯು ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ.
ಇಲ್ಲಿ ಮ.ಸಾ.ಅ. (c.d) ಎಂಬ ಸಂಕೇತವು c ಮತ್ತು d ಗಳ ಮ.ಸಾ.ಅ.ವನ್ನು ಸೂಚಿಸುತ್ತದೆ.
5. ಯಾವುದೇ ಧನ ಪೂರ್ಣಾಂಕ c ಯನ್ನು ಇನ್ನೊಂದು ಧನ ಪೂರ್ಣಾಂಕ b ಯಿಂದ ಭಾಗಿಸಿದಾಗ ಉಳಿಯುವ ಶೇಷ r ಎಂಬುದು, ಯಾವಾಗಲೂ ಭಾಜಕ b ಗಿಂತ ಕಡಿಮೆಯಾಗಿರುತ್ತದೆ.
6. ಒಂದು ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಯ ಆವಿಭಾಜ್ಯ ಅಪವರ್ತಿಸುವಿಕೆಯು ಅನನ್ಯವಾಗಿದ್ದು, ಅದರ ಅಪವರ್ತನಗಳನ್ನು ಬರೆಯುವ ಕ್ರಮಗಳು ವಿಭಿನ್ನವಾಗಿರಬಹುದು.
7. ಅಂಕಗಣಿತದ ಮೂಲ ಪ್ರಮೇಯ: ಪ್ರತಿಯೊಂದು ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಯನ್ನು ಅವಿಭಾಜ್ಯಗಳ ಗುಣಲಬ್ಧವಾಗಿ ವ್ಯಕ್ತಪಡಿಸಬಹುದು (ಅಪವರ್ತಿಸಬಹುದು) ಮತ್ತು ಈ ಅಪವರ್ತಿಸುವಿಕೆಯು, ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನೆಗಳ ಘಟಿಸುವ ಕ್ರಮವನ್ನು ಹೊರತುಪಡಿಸಿ ಅನನ್ಯವಾಗಿರುತ್ತದೆ.
8. ವಾಸ್ತವವಾಗಿ ಯಾವುದೇ ಎರಡು ಧನ ಪೂರ್ಣಾಂಕ a ಮತ್ತು b ಗಳಿಗೆ, ಮ.ಸಾ.ಅ. (a,b) x ಲ.ಸಾ.ಅ (a, b)= a x b ಆಗಿರುವುದನ್ನು ನಾವು ತಾಳೆ ನೋಡಬಹುದು.
9. ಒಂದು ಸಂಯುಕ್ತ ಸಂಖ್ಯೆ xನ್ನು ನಾವು x = p1p2…pn ಎಂದು ಅಪವರ್ತಿಸಬಹುದು. ಇಲ್ಲಿ p1 p2…. pn. ಇವು ಅವಿಭಾಜ್ಯಗಳಾಗಿವೆ ಮತ್ತು ಅವುಗಳನ್ನು ಏರಿಕೆ ಕ್ರಮದಲ್ಲಿ ಬರೆಯಲಾಗಿದೆ. ಅಂದರೆ P1 < P2 <…..< Pn. ನಾವು ಒಂದೇ ರೀತಿಯ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಸಂಯೋಜಿಸಿದರೆ, ಆವಿಭಾಜ್ಯಗಳ ಘಾತಗಳು ನಮಗೆ ದೊರೆಯುತ್ತವೆ.
10. ಒಂದು ಭಾಗಲಬ್ಧ ಮತ್ತು ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯ ಮೊತ್ತ ಅಥವಾ ವ್ಯತ್ಯಾಸವು ಅಭಾಗಲಬ್ಧವಾಗಿರುತ್ತದೆ.
11. x ಎಂಬುದು ಅಂತ್ಯಗೊಳ್ಳುವ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯನ್ನು ಹೊಂದಿರುವ ಒಂದು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಆಗಿರಲಿ. ಆಗ x ನ್ನು p/q ರೂಪದಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಬಹುದು. ಇಲ್ಲಿ p ಮತ್ತು q ಗಳು ಸಹ ಅವಿಭಾಜ್ಯಗಳು ಮತ್ತು q ದ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳು 2n5m ರೂಪದಲ್ಲಿರುತ್ತವೆ. ಇಲ್ಲಿ n,m ಗಳು ಋಣಾತ್ಮಕವಲ್ಲದ ಪೂರ್ಣಾಂಕಗಳಾಗಿವೆ.
12. ಶೂನ್ಯವಲ್ಲದ ಒಂದು ಭಾಗಲಬ್ಧ ಮತ್ತು ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯ ಗುಣಲಬ್ಧ ಮತ್ತು ಭಾಗಲಬ್ಬವು ಅಭಾಗಲಬ್ಧವಾಗಿರುತ್ತದೆ.
ಇತರೆ ವಿಷಯಗಳು :
10ನೇ ತರಗತಿ ಗಣಿತ ನಿರ್ದೇಶಾಂಕ ರೇಖಾಗಣಿತ ನೋಟ್ಸ್
10ನೇ ತರಗತಿ ಗಣಿತ ಬಹುಪದೋಕ್ತಿಗಳು ನೋಟ್ಸ್
