10ನೇ ತರಗತಿ ಗಣಿತ ಪೂರಕ ಪರೀಕ್ಷಾ ಪ್ರಶ್ನೆಪತ್ರಿಕೆ ಜೂನ್ / ಜುಲೈ – 2022, SSLC Supplementary Exam Question Paper 2022 (ಉತ್ತರಸಹಿತ) SSLC Supplementary Exam Question Paper 2022 Pdf download karnataka sslc question papers with answers pdf sslc previous year question papers with answers pdf download sslc previous year question papers with answers pdf download kannada medium June 2022 SSLC Supplementary exam Key answers Karnataka SSLC question papers with answers PDF 10th standard maths previous year question papers with answers pdf download

SSLC Supplementary Exam Question Paper 2022
I. ಬಹು-ಆಯ್ಕೆ ಪ್ರಶ್ನೆಗಳು: 8 x 1= 8
1. x – y = 8 ಮತ್ತು 3x – 3y = 16 ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ ಜೋಡಿಗಳು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು
(A) ಛೇದಿಸುವ ರೇಖೆಗಳು
(B) ಸಮಾಂತರ ರೇಖೆಗಳು
(C) ಲಂಬ ರೇಖೆಗಳು
(D) ಐಕ್ಯಗೊಳ್ಳುವ ರೇಖೆಗಳು
ಉತ್ತರ:
(B) ಸಮಾಂತರ ರೇಖೆಗಳು
2. 5, 3, 1, -1,……… ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ
(A) -2 (B) 2
(C) -3 (D) 5
ಉತ್ತರ:
(A) -2
3. x(x + 1) = 5 ಇದು ಬಂದು
(A) ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ
(B) ವರ್ಗ ಸಮೀಕರಣ
(C) ಘನ ಸಮೀಕರಣ
(D) ವರ್ಗ ಬಹುಪದೋಕ್ತಿ
ಉತ್ತರ:
(B) ವರ್ಗ ಸಮೀಕರಣ
4. 1 + tan2 θ ಗೆ ಸಮನಾದುದು
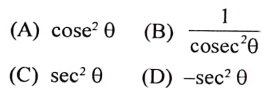
ಉತ್ತರ:
(c) sec2 θ
5. cot 90° ಯ ಬೆಲೆಯು
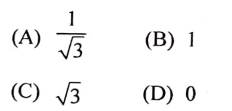
ಉತ್ತರ:
(D) 0
6. ಮೂಲಬಿಂದು ಮತ್ತು ಬಿಂದು P (a,b) ಗಳ ನಡುವಿನ ದೂರವು
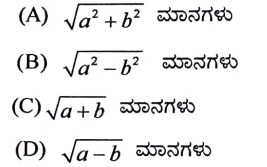
ಉತ್ತರ:
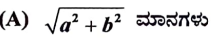
7. ಕೊಟ್ಟಿರುವ ಚಿತ್ರದಲ್ಲಿ ಛೇದಕವು
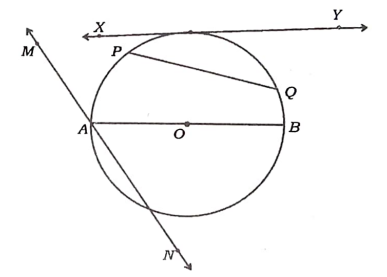
(A) AB (B) PQ
(C) XY (D) MN
ಉತ್ತರ:
(D) MN
8. ತ್ರಿಜ್ಯ ‘r’ ಮಾನ ಆಗಿರುವ ಒಂದು ಗೋಳದ ಘನಫಲವು

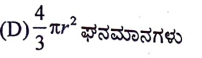
ಉತ್ತರ:

II. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ: 8 x 1 = 8
(ಪ್ರಶ್ನೆ ಸಂಖ್ಯೆ 9 ರಿಂದ 16 ರವರೆಗೆ ನೇರ ಉತ್ತರಕ್ಕೆ ಪೂರ್ಣ ಅಂಕಗಳನ್ನು ನೀಡುವುದು)
9. a1x + b1y + c1 =0 ಮತ್ತು a2x + b2y + c2 = 0 ಈ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ ಜೋಡಿಗಳು ಅಸ್ಥಿರವಾಗಿದ್ದರೆ, ಅವು ಹೊಂದಿರುವ ಪರಿಹಾರಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು?
ಉತ್ತರ:
ಯಾವುದೇ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ.
10. ಸಮಾಂತರ ಶ್ರೇಢಿ ಎಂದರೇನು?
ಉತ್ತರ:
ಮೊದಲ ಪದವನ್ನು ಹೊರತುಪಡಿಸಿ ಪ್ರತಿಯೊಂದು ಪದವನ್ನು ಪಡೆಯಲು ಅದರ ಹಿಂದಿನ ಪದಕ್ಕೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯನ್ನು ಕೂಡಿಸುವುದರಿಂದ ಪಡೆಯುವ ಸಂಖ್ಯಾಪಟ್ಟಿಯೇ ಸಮಾಂತರ ಶ್ರೇಢಿ.
11. ಒಂದು ವರ್ಗ ಸಮೀಕರಣದ ಆದರ್ಶ ರೂಪವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
ax2 + bx + c = 0
12. ಚಿತ್ರದಲ್ಲಿ ABC ಒಂದು ಲಂಬಕೋನ ತ್ರಿಭುಜ /C= 30° ಮತ್ತು AB = 12cm ಆದರೆ, AC ಯ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
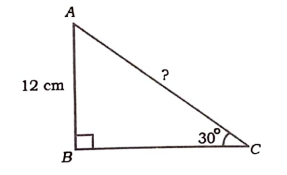
ಉತ್ತರ:
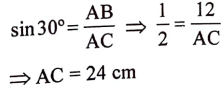
13. A(x1, y1) ಮತ್ತು B(x2, y2) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡವನ್ನು P ಬಿಂದುವು m1m2 ಅನುಪಾತದಲ್ಲಿ ಆಂತರಿಕವಾಗಿ ವಿಭಾಗಿಸಿದೆ. P ಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
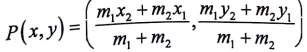
14. 4, 5, 5, 6, 7, 7, 6, 7, 5, 5 ಈ ದತ್ತಾಂಶಗಳ ಬಹುಲಕ (ರೂಢಿ ಬೆಲೆ) ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಬಹುಲಕ = 5
15. ‘ಮೂಲ ಸಮಾನುಪಾತತೆಯ ಪ್ರಮೇಯ” (ಥೇಲ್ಸ್ ಪ್ರಮೇಯ)ವನ್ನು ನಿರೂಪಿಸಿ.
ಉತ್ತರ:
ತ್ರಿಭುಜದ ಎರಡು ಬಾಹುಗಳನ್ನು ಎರಡು ವಿಭಿನ್ನ ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವಂತೆ ಒಂದು ಬಾಹುವಿಗೆ ಸಮಾನಾಂತರವಾಗಿ ಎಳೆದ ಸರಳರೇಖೆಯು ಉಳಿದೆರಡು ಬಾಹುಗಳನ್ನು ಸಮಾನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುತ್ತದೆ.
16. ಎರಡು ವೃತ್ತ ಪಾದದ ತ್ರಿಜ್ಯಗಳು r1 ಮತ್ತು r2‘ ಎತ್ತರ h’ ಆಗಿರುವ ಶಂಕುವಿನ ಭಿನ್ನಕದ ಘನಫಲ (V) ವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರ ಬರೆಯಿರಿ.
ಉತ್ತರ:
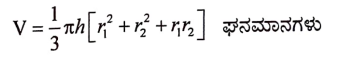
III. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ. 8 x 2 = 16
17. ಕೊಟ್ಟಿರುವ ಈ ಸಮೀಕರಣಗಳನ್ನು ವರ್ಜಿಸುವ ವಿಧಾನದಿಂದ ಬಿಡಿಸಿ:
2x + 3y = 7
2x + y = 5
ಉತ್ತರ:

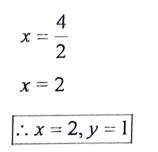
18. 2, 5, 8,………… ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯ 12ನೇ ಪದವನ್ನು ಸೂತ್ರ ಉಪಯೋಗಿಸಿ ಕಂಡು ಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
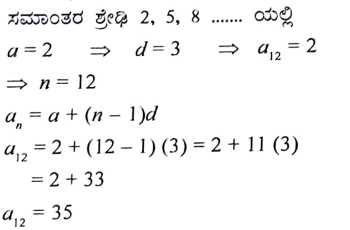
19. 7, 11, 15………, ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯ 16 ಪದಗಳವರೆಗಿನ ಮೊತ್ತವನ್ನು ಸೂತ್ರ ಉಪಯೋಗಿಸಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
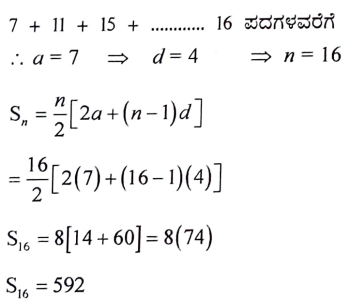
ಅಥವಾ
3, 6, 9,… ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಎಷ್ಟು ಪದಗಳನ್ನು ಕೂಡಿದಾಗ ಮೊತ್ತ 165 ಆಗುತ್ತದೆ ಎಂದು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:


20. 4x2 – 12x + 9 = 0 ಈ ಸಮೀಕರಣ ಶೋಧಕದ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿದು, ಮೂಲಗಳ ಸ್ವಭಾವವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
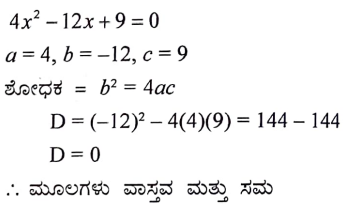
21. x2 – 3x + 1 = 0 ಈ ಸಮೀಕರಣದ ಮೂಲಗಳನ್ನು ವರ್ಗಸಮೀಕರಣದ ಸೂತ್ರ ಉಪಯೋಗಿಸಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
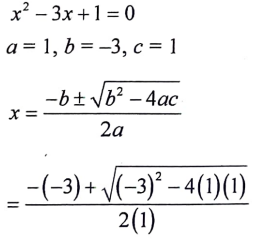
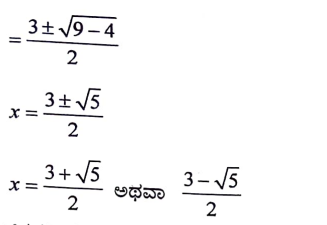
22. ಚಿತ್ರದಲ್ಲಿ ABC ಒಂದು ಲಂಬಕೋನ ತ್ರಿಭುಜ AB = 24cm, BC = 7 cm ಮತ್ತು AC = 25 cm , sin α ಮತ್ತು cos α ಗಳ ಬೆಲೆಗಳನ್ನು ಬರೆಯಿರಿ.
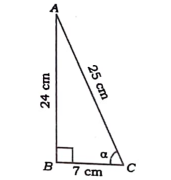
ಉತ್ತರ:
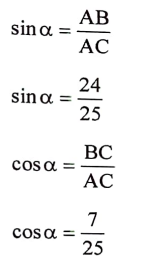
23. P(2,3) Q (4, 1) ಈ ಬಿಂದುಗಳ ನಡುವಿನ ದೂರವನ್ನು ‘ದೂರ ಸೂತ್ರ’ ಉಪಯೋಗಿಸಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
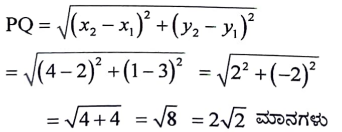
ಅಥವಾ
A(-6, 10) ಮತ್ತು B(3,-8) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡ P(-4, 6) ಯನ್ನು ಬಿಂದುವು ವಿಭಾಗಿಸುವ ಅನುಪಾತವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಭಾಗ ಪ್ರಮಾಣ ಸೂತ್ರದ ಪ್ರಕಾರ
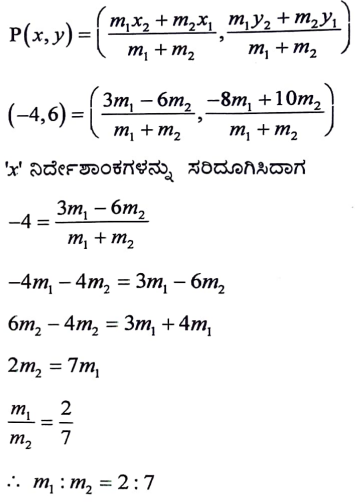
24. 84 ಸೆಂ.ಮೀ. ಉದ್ದವಿರುವ ಒಂದು ರೇಖಾಖಂಡವನ್ನು ಎಳೆದು, ಅದನ್ನು ಜ್ಯಾಮಿತಿ ರಚನೆಯಿಂದ 1 : 3 ಅನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸಿ.
ಉತ್ತರ:

IV. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ. 9 x 3 = 27
25. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೂರನೇ ಪದ 16 ಆಗಿದೆ ಮತ್ತು ಅದರ 7ನೇ ಪದವು 5ನೇ ಪದಕ್ಕಿಂತ 12 ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಆ ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

26. ಮೂರು ವರ್ಷಗಳ ಹಿಂದಿನ ರೆಹಮಾನನ ವಯಸು (ವರ್ಷಗಳಲ್ಲಿ) ಮತ್ತು 5 ವರ್ಷಗಳ ನಂತರದ ಅವನ ವಯಸ್ಸು ಇವುಗಳ ವ್ಯತ್ನಮಗಳ ಮೊತ್ತ 1/3 ಆದರೆ, ಅವನ ಈಗಿನ ವಯಸ್ಸನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ರೆಹಮಾನನ ಈಗಿನ ವಯಸ್ಸು ‘x’ವರ್ಷಗಳಾಗಿರಲಿ
3 ವರ್ಷಗಳ ಹಿಂದೆ ರೆಹಮಾನನ ವಯಸ್ಸು (x – 3) 5 ವರ್ಷಗಳ
ನಂತರ ರೆಹಮಾನನ ವಯಸ್ಸು (x + 5) ವರ್ಷಗಳು
ದತ್ತ ನಿಬಂಧನೆಯ ಪ್ರಕಾರ,
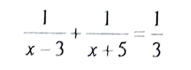
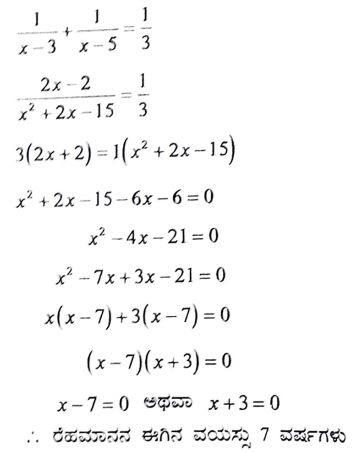
ಅಥವಾ
ಒಂದು ರೈಲು 360km ದೂರವನ್ನು ಏಕರೂಪ ಜವದೊಂದಿಗೆ ಕ್ರಮಿಸುತ್ತದೆ. ಅದರ ಜವವು 5km/h ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಅಷ್ಟೇ ದೂರವನ್ನು ಕ್ರಮಿಸಲು ಅದು 1 ಗಂಟೆ ಕಡಿಮೆ ಸಮಯ ತೆಗೆದುಕೊಳ್ಳುತ್ತಿತ್ತು. ರೈಲಿನ ಜವವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ರೈಲಿನ ಜವ ‘x’ km/h ಆಗಿರಲಿ
ರೈಲು ಚಲಿಸಿದ ದೂರ 360 km
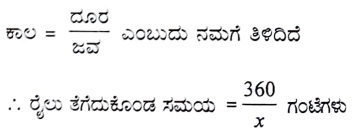
ರೈಲಿನ ಜನ 5 km/hr ಹೆಚ್ಚಾಗಿದ್ದರೆ, ರೈಲಿನ ಜವವು (x + 5) km/hr ಆಗಿರುತ್ತಿತ್ತು
ಆಗ ರೈಲು ತೆಗೆದುಕೊಳ್ಳುವ ಸಮಯ ಗಂಟೆಗಳು ಆಗುತ್ತಿತ್ತು.
ದತ್ತ ನಿಬಂಧನೆಯ ಪ್ರಕಾರ,
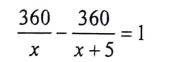
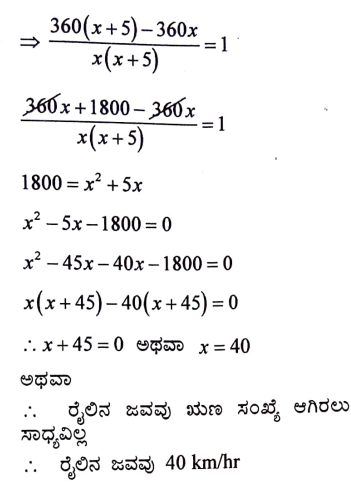
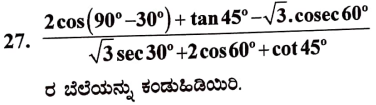
ಉತ್ತರ:
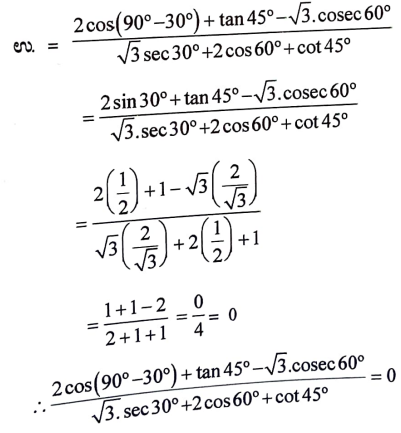
28. ಒಂದು ಗೋಪುರ ಮತ್ತು ಒಂದು ಕಟ್ಟಡ ಒಂದೇ ಸಮತಟ್ಟಾದ ನೆಲದ ಮೇಲೆ ನೇರವಾಗಿ ನಿಂತಿದೆ. ಗೋಪುರದ ಪಾದದಿಂದ ಕಟ್ಟಡದ ಮೇಲ್ತುದಿಯನ್ನು ನೋಡಿದಾಗ ಉನ್ನತ ಕೋನವು 30° ಮತ್ತು ಕಟ್ಟಡದ ಪಾದದಿಂದ ಗೋಪುರದ ಮೇಲ್ತುದಿಗೆ ಉನ್ನತಕೋನವು 60° ಇದೆ. ಗೋಪುರದ ಎತ್ತರ 50m ಇದ್ದರೆ ಕಟ್ಟಡದ ಎತ್ತರ ಕಂಡುಹಿಡಿಯಿರಿ.
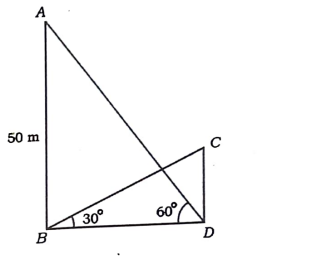
ಉತ್ತರ:


ಅಥವಾ
ಒಂದು ರೈಲು 360km ದೂರವನ್ನು ಏಕರೂಪ ಜವದೊಂದಿಗೆ ಕ್ರಮಿಸುತ್ತದೆ. ಅದರ ಜನವು 5km/h ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಅಷ್ಟೇ ದೂರವನ್ನು ಕ್ರಮಿಸಲು ಅದು 1 ಗಂಟೆ ಕಡಿಮೆ ಸಮಯ ತೆಗೆದುಕೊಳ್ಳುತ್ತಿತ್ತು. ರೈಲಿನ ಜವವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:


29. P(2,3) Q(4, k) 2 R(6, – 3) ಬಿಂದುಗಳು ಸರಳರೇಖಾಗತವಾಗಿದ್ದರೆ ‘k’ ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
P(2,3) Q(4, k) ಮತ್ತು R(6, – 3)
ಈ ಬಿಂದುಗಳು ಸರಳರೇಖಾಗತವಾಗಿರುವುದರಿಂದ ಇವುಗಳಿಂದ ಉಂಟಾದ ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವು ಸೊನ್ನೆಯಾಗಿರುತ್ತದೆ.

ಅಥವಾ
ಒಂದು ವೃತ್ತಕೇಂದ್ರವು P(2, 3) ಆಗಿದ್ದು, ಆ ವೃತ್ತವು A(4,3) ಮತ್ತು B(x, 5) ಬಿಂದುಗಳ ಮೂಲಕ ಹಾದು ಹೋದರೆ ನ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
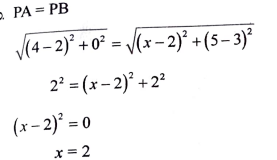
30. ಈ ಕೆಳಗೆ ನೀಡಿರುವ ದತ್ತಾಂಶಗಳಿಗೆ ನೇರ ವಿಧಾನದಿಂದ ಸರಾಸರಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
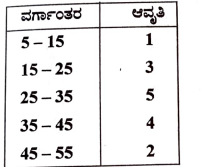
ಉತ್ತರ:


ಅಥವಾ
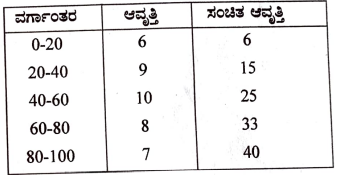
ಈ ಕೆಳಗೆ ದತ್ತಾಂಶಗಳಿಗೆ ಮಧ್ಯಾಂಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ:
ವರ್ಗಾಂತರ ಆವೃತಿ
0-20 6
20-40 9
40-60 10
60-80 8
80-100 7
ಉತ್ತರ:
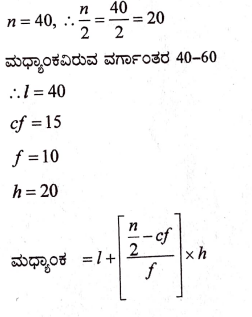
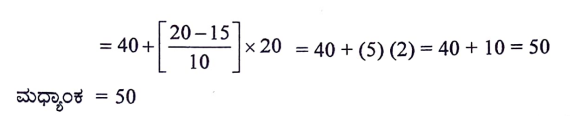
31. ಈ ಕೆಳಗಿನ ಕೋಷ್ಟಕದಲ್ಲಿ ಒಂದು ಶಾಲೆಯ X ನೇ ತರಗತಿಯ 60 ವಿದ್ಯಾರ್ಥಿಗಳ ಎತ್ತರದ ಮಾಹಿತಿಯನ್ನು ನೀಡಲಾಗಿದೆ. ಈ ದತ್ತಾಂಶಗಳಿಗೆ ಕಡಿಮೆ ವಿಧಾನದ ಓಜೀವ್ ರಚಿಸಿ:
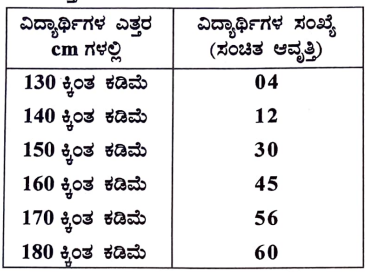
ಉತ್ತರ:
32. “ಬಾಹ್ಯ ಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳ ಉದ್ದವು ಸಮವಾಗಿರುತ್ತದೆ” ಎಂದು ಸಾಧಿಸಿ.
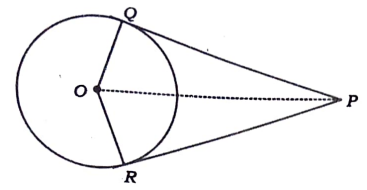
ಉತ್ತರ:
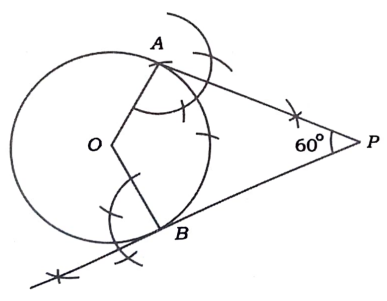
33. 3em ತ್ರಿಜ್ಯದ ವೃತ್ತಕ್ಕೆ, ಸ್ಪರ್ಶಕಗಳ ನಡುವಿನ ಕೋನ 60° ಇರುವಂತೆ ಒಂದು ಜೊತೆ ಸ್ಪರ್ಶಕಗಳನ್ನು ರಚಿಸಿ,
ಉತ್ತರ:
ತ್ರಿಜ್ಯಗಳ ನಡುವಿನ ಕೋನ = 1800 – 600 = 1200
V. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ: 4 x 4 = 16
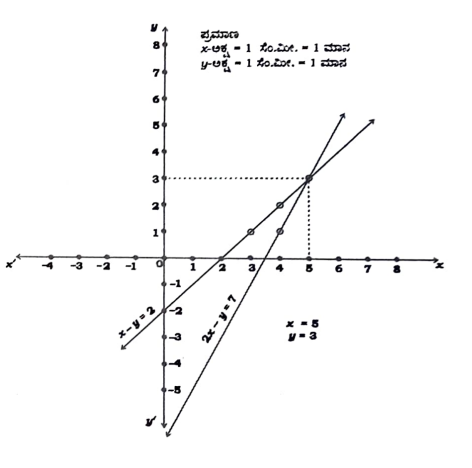
34. ಕೊಟ್ಟಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ, ನಕ್ಷೆಯ ವಿಧಾನದಿಂದ ಪರಿಹಾರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ:
2x – y = 7
x – y = 2
ಉತ್ತರ:
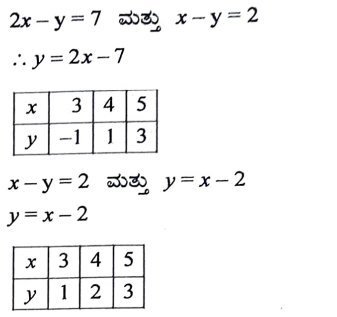
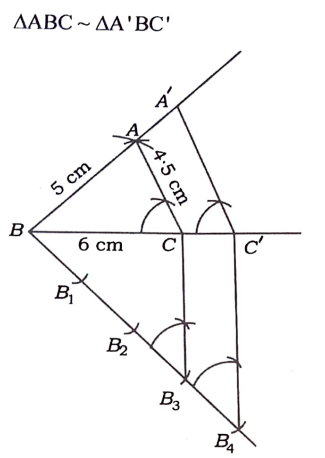
35. BC = 6cm AB-5cm ಮತ್ತು AC = 4.5cm ಇರುವಂತೆ ತ್ರಿಭುಜ ABC ಯನ್ನು ರಚಿಸಿ, ನಂತರ ಮತ್ತೊಂದು ತ್ರಿಭುಜವನ್ನು ಅದರ ಬಾಹುಗಳು ತ್ರಿಭುಜ ABC ಯ ಅನುರೂಪ ಬಾಹುಗಳ 4/3 ರಷ್ಟಿರುವಂತೆ ರಚಿಸಿ.
ಉತ್ತರ:
36. ABCD ಯ 14cm ಬಾಹುವುಳ್ಳ ಚೌಕವಾಗಿದೆ. P, Q, R ಮತ್ತು S ಗಳು ಈ ಚೌಕದ ಬಾಹುಗಳ ಮಧ್ಯಬಿಂದುಗಳಾಗಿವೆ. ಚೌಕದ ಬಾಹುಗಳ ಮಧ್ಯಬಿಂದುಗಳನ್ನು ಸ್ಪರ್ಶಿಸುವಂತೆ ಚೌಕದ ಒಳಗೆ ವೃತ್ತವನ್ನು ಎಳೆಯಾಲಾಗಿದೆ. PQ, QR, RS ಮತ್ತು PS ವೃತ್ತದ ಕಂಸಗಳಾಗಿವೆ. ಚಿತ್ರದಲ್ಲಿ ಛಾಯೆಗೊಳಿಸಿದ ಭಾಗದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.


37. ಪಾದದ ತ್ರಿಜ್ಯ 18cm ಮತ್ತು ಎತ್ತರ 32em ಇರುವ ಒಂದು ಸಿಲಿಂಡರಿನಾಕಾರದ ಪಾತ್ರೆಯಲ್ಲಿ ಪೂರ್ಣವಾಗಿ ಮರಳನ್ನು ತುಂಬಿದೆ. ಪಾತ್ರೆಯಲ್ಲಿರುವ ಮರಳನ್ನು ಪೂರ್ತಿಯಾಗಿ ನೆಲದ ಮೇಲೆ ಸುರಿದಾಗ ಅದು ಶಂಕುವಿನಾಕಾರದ ಮರಳಿನ ರಾಶಿಯನ್ನು ಉಂಟುಮಾಡಿದೆ. ಶಂಕುವಿನಾಕಾರದ ರಾಶಿಯ ಎತ್ತರವು 24cm ಆದಾಗ ಶಂಕುವಿನಾಕಾರದ ಮರಳಿನ ರಾಶಿಯ ಪಾದದ ತ್ರಿಜ್ಯ ಮತ್ತು ಓರೆ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
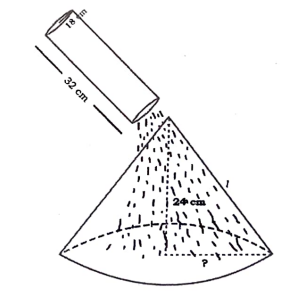
ಉತ್ತರ:

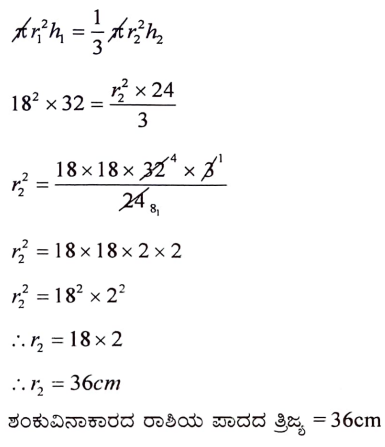
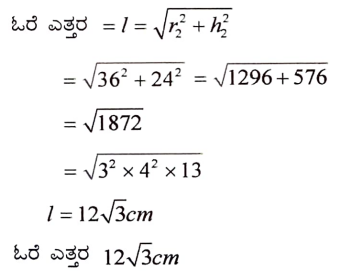
ಅಥವಾ
ಒಂದು ಅರ್ಧಗೋಳದ ಮೇಲೆ ಅದೇ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವ ಒಂದು ಶಂಕುವನ್ನು ಕೂಡಿಸಿ ಒಂದು ಆಟಿಕೆಯನ್ನು ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿದಂತೆ ಮಾಡಿದೆ. ಅವೆರೆಡರ ವೃತ್ತಾಕಾರದ ಪಾದದ ತ್ರಿಜ್ಯವು 21cm ಆಗಿದೆ. ಆಟಿಕೆಯ ಒಟ್ಟು ಎತ್ತರವು 49cm ಆಗಿದೆ. ಆ ಆಟಿಕೆಯ ಮೇಲೆ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
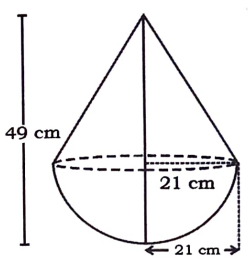
ಉತ್ತರ:

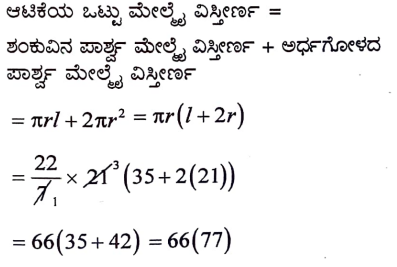

VI. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ: 1 x 5 = 5
38. “ಎರಡು ತ್ರಿಭುಜಗಳಲ್ಲಿ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾದರೆ, ಅವುಗಳ ಅನುರೂಪ ಬಾಹುಗಳ ಅನುಪಾತಗಳು ಸಮ (ಅಥವಾ ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ) ಆದ್ದರಿಂದ ಆ ತ್ರಿಭುಜಗಳು ಸಮರೂಪವಾಗಿರುತ್ತದೆ.’ ಎಂದು ಸಾಧಿಸಿ.
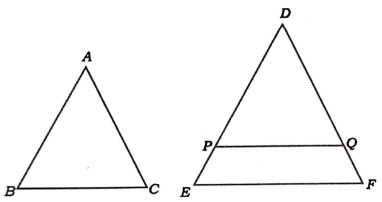
ಉತ್ತರ:


