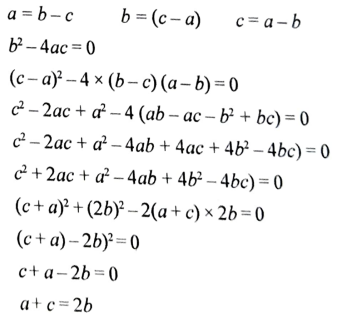10ನೇ ತರಗತಿ ಗಣಿತ ಪೂರಕ ಪರೀಕ್ಷಾ ಪ್ರಶ್ನೆಪತ್ರಿಕೆ ಮಾರ್ಚ್ – 2019, SSLC Supplementary Exam Question Paper 2019 (ಉತ್ತರಸಹಿತ) 10ನೇ ತರಗತಿ ಗಣಿತ ಮಾದರಿ ಪ್ರಶ್ನೆ ಪತ್ರಿಕೆಗಳು 2019 pdf 10th standard maths exam question paper with solution sslc 2019 maths question paper with answer sslc question paper 2019 karnataka pdf with answers maths maths board paper 2019 class 10 solutions pdf download 2019 maths question paper solved karnataka sslc question papers with answers pdf

SSLC Preparatory Exam Question Paper 2019
I. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಅಥವಾ ಅಪೂರ್ಣ ಹೇಳಿಕೆಗಳಿಗೆ ನಾಲ್ಕು ಪರ್ಯಾಯ ಉತ್ತರಗಳನ್ನು ನೀಡಲಾಗಿದೆ. ಅವುಗಳಲ್ಲಿ ಸರಿಯಾದ ಉತ್ತರವನ್ನು ಆರಿಸಿ. ಕ್ರಮಾಕ್ಷರದೊಡನೆ ಪೂರ್ಣ ಉತ್ತರವನ್ನು ಬರೆಯಿರಿ. 8 x 1 = 8
1. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ nನೇ ಪದ 5n +3 ಆದಾಗ ಸಮಾಂತರ ಶ್ರೇಢಿಯ 3ನೇ ಪದವು
a) 11 b) 18 c) 12 d) 13
ಉತ್ತರ:
a) 18
2. ಚಿತ್ರದಲ್ಲಿ ‘O’ ಕೇಂದ್ರವುಳ್ಳ ವೃತ್ತಕ್ಕೆ PA, PC ಮತ್ತು CD ಗಳು ಸ್ಪರ್ಶಕಗಳಾಗಿವೆ. AP = 3cm CD = Scm ಆದಾಗ PC ಯ ಉದ್ದವು.
(a) 3cm (b) 5cm (c) 8cm (d) 2cm
ಉತ್ತರ:
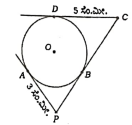
(c) 8cm
3. a1x + b1y + c1 = 0 ಹಾಗೂ a2x + b2y + c2 = 0 ರೂಪದ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳಿಗೆ ಎಳೆದ ರೇಖೆಗಳು ಪರಸ್ಪರ ಐಕ್ಯಗೊಂಡರೆ ಈ ಕೆಳಗಿನವುಗಳಲ್ಲಿ ಸರಿಯಾದ ಸಂಬಂಧವು.
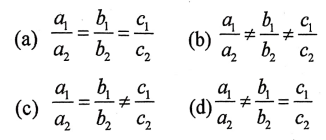
ಉತ್ತರ:
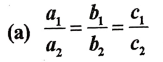
4. ಮೂಲಬಿಂದು ಮತ್ತು (x,y) ನಿರ್ದೇಶಾಂಕಗಳ ನಡುವಿನ ದೂರವು
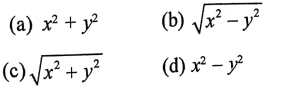
ಉತ್ತರ:
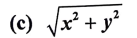
5. 72 ಮತ್ತು 120ರ ಮ.ಸಾ.ಅ 24 ಆದರೆ, ಅವುಗಳ ಲ.ಸಾ.ಅ
(a) 36 (b) 720 (c) 360 (d) 72
ಉತ್ತರ:
(c) 360
7. sin 300 + cos 600 ಯ ಬೆಲೆಯು

ಉತ್ತರ:
(d) 1
7. ಕೊಟ್ಟಿರುವ ನಕ್ಷೆ y = P(x) ನಲ್ಲಿ ಶೂನ್ಯತೆಗಳ ಸಂಖ್ಯೆಯು
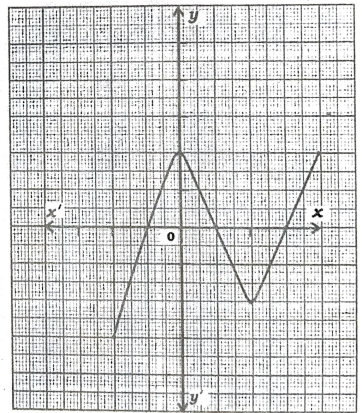
(a) 4 (b) 3 (c) 2 (d) 7
ಉತ್ತರ:
(b) 3
8. 1 ರಿಂದ 6ರವರೆಗಿನ ಸಂಖ್ಯೆಗಳನ್ನು ಹೊಂದಿರುವ ಒಂದು ಘನಾಕೃತಿಯ ದಾಳವನ್ನು ಒಂದು ಬಾರಿ ಉರುಳಿಸಿದಾಗ, ಬೆಸ ಸಂಖ್ಯೆ ಮೇಲೆ ಬರುವ ಸಂಭವನೀಯತೆಯು,
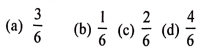
ಉತ್ತರ:
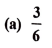
II. ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಉತ್ತರಿಸಿ.
9. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲನೆ ಪದವು ‘a’ ಮತ್ತು ಕೊನೆಯ ಪದವು ‘an‘ ಆದಾಗ, ಆ ಶ್ರೇಢಿಯ ಮೊದಲ ‘n’ ಪದಗಳವರೆಗಿನ ಮೊತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
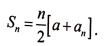
10. ಎರಡು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ ಪರಿಹಾರ ಇರುವುದಿಲ್ಲ (ಅಸ್ಥಿರವಾಗಿದ್ದರೆ). ಆ ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು ಎಂತಹ ರೇಖೆಗಳಾಗಿರುತ್ತದೆ ಎಂದು ಬರೆಯಿರಿ.
ಉತ್ತರ:
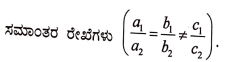
11. ವೃತ್ತ ಕೇಂದ್ರದಲ್ಲಿ ಉಂಟಾದ ಕೋನವು ‘9’ ಡಿಗ್ರಿಯಾದಾಗ ತ್ರಿಜ್ಯಾಂತರ ಖಂಡದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
ತ್ರಿಜ್ಯಾಂತರ ಖಂಡದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರ
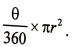
12. 96ನ್ನು ಅವುಗಳ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳಾಗಿ ಬರೆಯಿರಿ.
ಉತ್ತರ:
96=3×2×2×2×2×2
13. P(x) = x²+2x² – 5x – 6 ಬಹುಪದೋಕ್ತಿಯ ಮಹತ್ತಮ ಘಾತ (ಡಿಗ್ರಿ)ವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
3
14. ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ ∠ABC = 90° ಮತ್ತು ∠ACB = 30° ಆದಾಗ, AB: AC ಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ
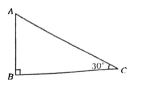
ಉತ್ತರ:
III. ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಉತ್ತರಿಸಿ.
15. ಈ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ ಪರಿಹಾರವನ್ನು (2)
x + y = 14
x – y = 4
ಉತ್ತರ:
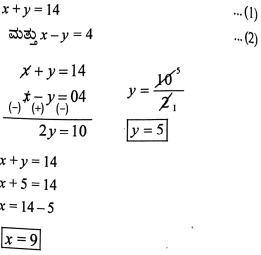
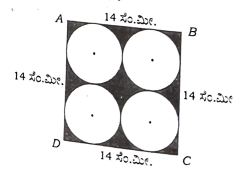
16. ABCD ಯು 14cm ಬಾಹುವಿರುವ ಒಂದು ಚೌಕ. ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಇದರಲ್ಲಿ ನಾಲ್ಕು ಸರ್ವಸಮ ವೃತ್ತಗಳನ್ನು ರಚಿಸಲಾಗಿದೆ. ಹಾಗಾದರೆ ಛಾಯೆಗೊಳಿಸಿದ ವಲಯದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (ವೃತ್ತಗಳು ಒಂದನ್ನೊಂದು ಬಾಹ್ಯವಾಗಿ ಸ್ಪರ್ಶಿಸುತ್ತದೆ ಮತ್ತು ಚೌಕದ ಬಾಹುಗಳನ್ನು ಸ್ಪರ್ಶಿಸುತ್ತವೆ).
ಉತ್ತರ:
a → ಚೌಕದ ಬಾಹು, r → ವೃತ್ತದ ತ್ರಿಜ್ಯ = 3.5 ಚೌಕದ ವಿಸ್ತೀರ್ಣ – 14
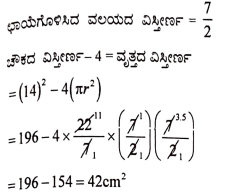
17. (2,3) ಮತ್ತು (4, 1) ಬಿಂದುಗಳ ನಡುವಿನ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
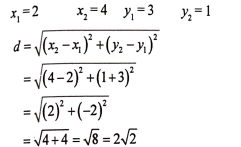
18. ಶೃಂಗ ಬಿಂದುಗಳು (1,-1), (-4, 6) 2 (-3,-5) ಆಗಿರುವ ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (2)
ಉತ್ತರ:
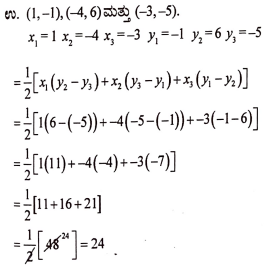
19. 5+ √3 ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
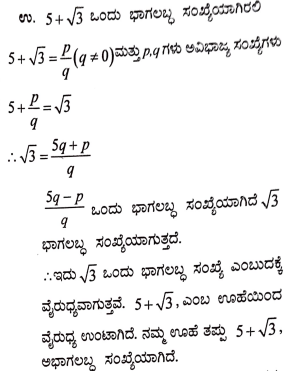
20. △ABC ~ ADEF ಮತ್ತು ಅವುಗಳ ವಿಸ್ತೀರ್ಣಗಳು ಕ್ರಮವಾಗಿ 64cm2 ಮತ್ತು 100cm2 ಗಳಾಗಿದ್ದು, EF= 12cm ಆದಾಗ BCಯ ಅಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
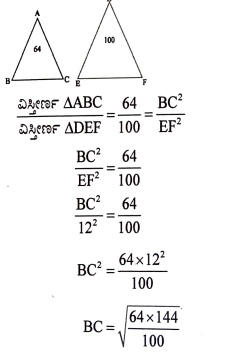
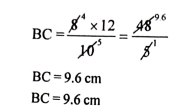
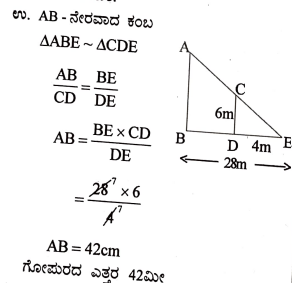
ಅಥವಾ
6 ಮೀಟರ್ ಎತ್ತರದ ನೇರವಾದ ಕಂಬವು ನೆಲದ ಮೇಲೆ 4 ಮೀಟರ್ ಉದ್ದದ ನೆರಳನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ. ಅದೇ ಸಮಯದಲ್ಲಿ ಅದೇ ನೆಲದ ಮೇಲಿನ ಒಂದು ಕಟ್ಟಡವು 28 ಮೀಟರ್ ಉದ್ದದ ನೆರಳನ್ನು ಉಂಟುಮಾಡಿದರೆ, ಆ ಕಟ್ಟಡದ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
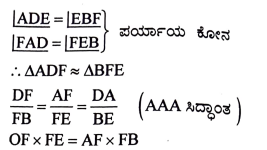
21. ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ABCD ಒಂದು ಸಮಾಂತರ ಚತುರ್ಭುಜ BC ಯ ಮೇಲೆ E ಒಂದು ಬಿಂದು, ಕರ್ಣ BD ಯು AE ಯನ್ನು F ನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ. ಹಾಗಾದರೆ DF x EF = FB x FA ಎಂದು ಸಾಧಿಸಿ.
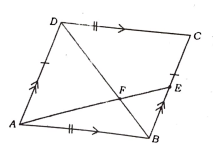
ಉತ್ತರ:
ಚಿತ್ರದಲ್ಲಿ △ADF ಮತ್ತು △BFE ಯಲ್ಲಿ
22. ಒಂದು ವರ್ಗ ಬಹುಪದೋಕ್ತಿ P(x) = ax2 + bx – 4 ರ ಶೂನ್ಯತೆಗಳ ಮೊತ್ತ ಮತ್ತು ಗುಣಲಬ್ಧಗಳು ಕ್ರಮವಾಗಿ 1/4 ಮತ್ತು -1 ಆಗಿದೆ. ಹಾಗಾದರೆ 4 ಮತ್ತು b ಗಳ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (2)
ಉತ್ತರ:
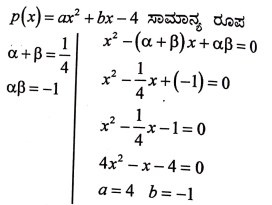
ಅಥವಾ
p(x) = 2x² + 2x +1 ನ್ನು g(x) = x + 2 ರಿಂದ ಭಾಗಿಸಿದಾಗ ಬರುವ ಭಾಗಲಬ್ಧ ಮತ್ತು ಶೇಷವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
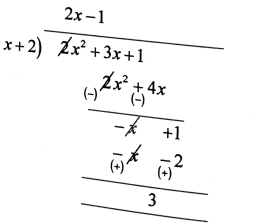
23. k ನ ಯಾವ ಬೆಲೆಗೆ ಬಹುಪದೋಕ್ತಿ P(x) = x2 – x – (2k + 2) ರ ಒಂದು ಶೂನ್ಯತೆಯು -4 ಆಗಿರುತ್ತದೆ ಎಂದು ಕಂಡುಹಿಡಿಯಿರಿ. (2)
ಉತ್ತರ:
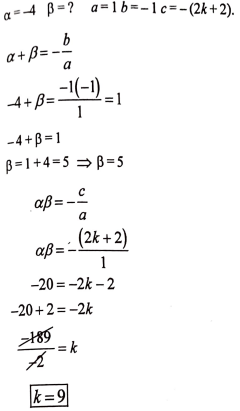
24. x2 – 3x – 10 = 0 ಸಮೀಕರಣವನ್ನು ಸೂತ್ರದ ಸಹಾಯದಿಂದ ಬಿಡಿಸಿ. (2)
ಉತ್ತರ:
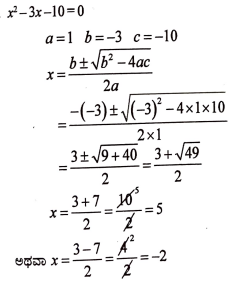
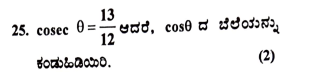
ಉತ್ತರ:
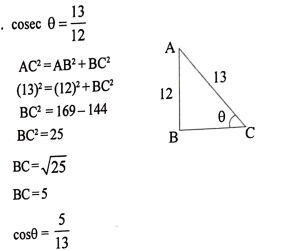
26. (tan A x sin A) + cos A = sec A ಎಂದು ತೋರಿಸಿ.
ಉತ್ತರ;

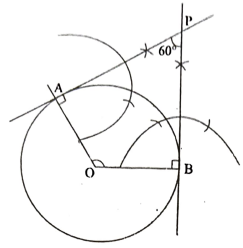
27. 3.5ಸೆಂ.ಮೀ ತ್ರಿಜ್ಯದ ಒಂದು ವೃತ್ತಕ್ಕೆ ಸ್ಪರ್ಶಕಗಳ ನಡುವಿನ ಕೋನ 60° ಇರುವಂತೆ ಒಂದು ಜೊತೆ ಸ್ಪರ್ಶಕಗಳನ್ನು ರಚಿಸಿ.
ಉತ್ತರ:
28. ಒಂದು ಪೆಟ್ಟಿಗೆಯಲ್ಲಿ 1 ರಿಂದ 90 ರವರೆಗಿನ ಸಂಖ್ಯೆಗಳು ನಮೂದಾಗಿರುವ 90 ಜಿಲ್ಲೆಗಳಿವೆ. ಪೆಟ್ಟಿಗೆಯಿಂದ ಒಂದು ಬಿಲ್ಲೆಯನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ತೆಗೆದರೆ, ಅದು ಒಂದು ಪೂರ್ಣ ವರ್ಗ ಸಂಖ್ಯೆ ಆಗಿರುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (2)
ಉತ್ತರ:

29. 9ಸೆಂ.ಮೀ ತ್ರಿಜ್ಯವುಳ್ಳ ಲೋಕ ಲೋಹದ ಗೋಳವನ್ನು ಕರಗಿಸಿ ಅದನ್ನು 6 ಸೆಂ.ಮೀ. ತ್ರಿಜ್ಯವಿರುವ ಸಿಲಿಂಡರಿನ ಆಕಾರದಲ್ಲಿ ಮರುರೂಪ ನೀಡಲಾಗಿದೆ. ಹಾಗಾದರೆ ಸಿಲಿಂಡರಿನ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (2)
ಉತ್ತರ:
ದತ್ತ ಗೋಳದ ತ್ರಿಜ್ಯ = 9cm
ಸಿಲಿಂಡರಿನ ತ್ರಿಜ್ಯ = 6cm
ಗೋಳದ ಘನಫಲ = ಸಿಲಿಂಡರಿನ ಘನಫಲ
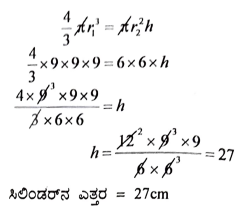
30. 64cm3 ಘನಫಲವನ್ನು ಹೊಂದಿರುವ ಎರಡು ವರ್ಗ ಘನಗಳ ಮುಖಗಳನ್ನು ಸೇರಿಸಿ ಒಂದು ಆಯತ ಘನಾಕೃತಿ ಮಾಡಿದೆ. ಈ ಆಯತ ಘನಾಕೃತಿಯ ಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (2)
ಉತ್ತರ:

IV. ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಉತ್ತರಿಸಿ.
31. “ಬಾಹ್ಯ ಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳ ಉದ್ದವು ಸಮನಾಗಿರುತ್ತದೆ.’ ಎಂದು ಸಾಧಿಸಿ. (3)
ಉತ್ತರ:
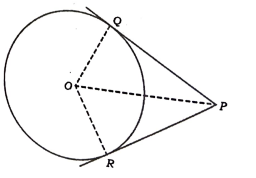
0 ವೃತ್ತ ಕೇಂದ್ರ ಮತ್ತು Pಯೂ ಬಾಹ್ಯಬಿಂದು PA ಮತ್ತು PB ಗಳು ಬಾಹ್ಯಬಿಂದುವಿನಿಂದ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳಾಗಿವೆ ನಾವು A ಮತ್ತು B ಎಂದು ಸಾಧಿಸಬೇಕಾಗಿದೆ.
ರಚನೆ: OP, OQ ಮತ್ತು OR ಗಳನ್ನು ಸೇರಿಸಿ.
ಸಾಧನೆ: ಲಂಬಕೋನ ತ್ರಿಭುಜ OPQ ಮತ್ತು OPR ಗಳಲ್ಲಿ
∠OQP = ∠ORP = 90° (ಲಂ, ವಿ, ಬಾ)
OQ= OR (ಒಂದೇ ವೃತ್ತದ ತ್ರಿಜ್ಯಗಳು)
OP= OQ (ಸಾಮಾನ್ಯ ಬಾಹು)
RHS ಸಮಾನತೆಯ ಪ್ರಕಾರ
△OQP ≅ △ORP (ಲಂ.ವಿ.ಬಾ)
ಆದ್ದರಿಂದ PQ = PR (ಪ ತಿ ಅ.ಬಾ)
ಅಥವಾ
ಎರಡು ಏಕಕೇಂದ್ರಿಯ ವೃತ್ತಗಳ ತ್ರಿಜ್ಯಗಳು 5cm ಮತ್ತು 3cm ಇರುವಂತೆ ರಚಿಸಿದೆ ಚಿಕ್ಕ ವೃತ್ತಕ್ಕೆ ಸ್ಪರ್ಶಿಸುವಂತೆ ಎಳೆದ ದೊಡ್ಡ ವೃತ್ತದ ಜ್ಯಾದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
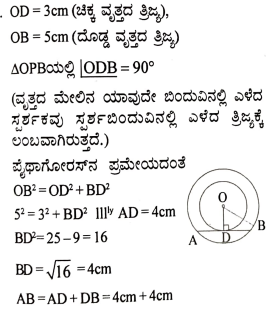
32. 5cm, 6cm ಮತ್ತು 7cm ಬಾಹುಗಳಿರುವ ಒಂದು ತ್ರಿಭುಜವನ್ನು ರಚಿಸಿ. ನಂತರ ಮತ್ತೊಂದು ತ್ರಿಭುಜವನ್ನು ಅದರ ಪ್ರತಿಯೊಂದು ಬಾಹುವು ಮೊದಲು ರಚಿಸಿದ ತ್ರಿಭುಜದ ಅನುರೂಪ ಬಾಹುಗಳ 3/5ರಷ್ಟಿರುವಂತೆ ರಚಿಸಿ.
ಉತ್ತರ:
33. ಈ ಕೆಳಗಿನ ಆವೃತ್ತಿ ವಿತರಣಾ ಪಟ್ಟಿಯಲ್ಲಿರುವ ದತ್ತಾಂಶಗಳಿಗೆ ಬಹುಲಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ: (3)

ಉತ್ತರ
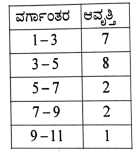
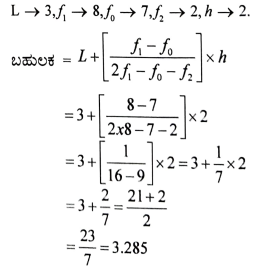
ಅಥವಾ
ಈ ಕೆಳಗಿನ ಆವೃತ್ತಿ ವಿತರಣಾ ಪಟ್ಟಿಯಲ್ಲಿರುವ ದತ್ತಾಂಶಗಳಿಗೆ ಮಧ್ಯಾಂಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ: (3)

ಉತ್ತರ
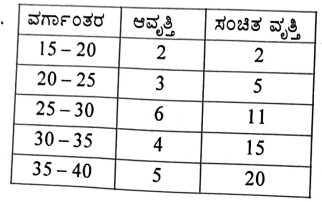
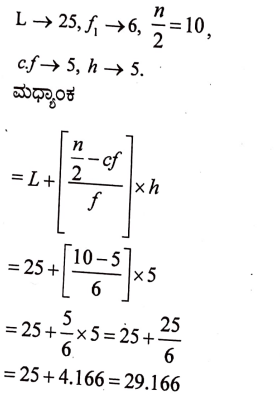
34. ಸಮತಟ್ಟಾದ ನೆಲದ ಮೇಲೆ 5 √3 ಮೀಟರ್ ಎತ್ತರದಲ್ಲಿರುವ ಒಂದು ನೇರ ಕಟ್ಟಡದ ಮೇಲಿನಿಂದ ಅದೇ ನೆಲದ ಮೇಲಿರುವ ಒಂದು ವಸ್ತುವನ್ನು ನೋಡಿದಾಗ ಉಂಟಾದ ಅವನತ ಕೋನವು 60° ಆಗಿರುತ್ತದೆ. ಹಾಗಾದರೆ ಕಟ್ಟಡದ ಬುಡದಿಂದ ವಸ್ತುವಿಗಿರುವ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (3)
ಉತ್ತರ:
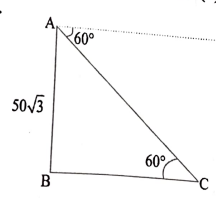
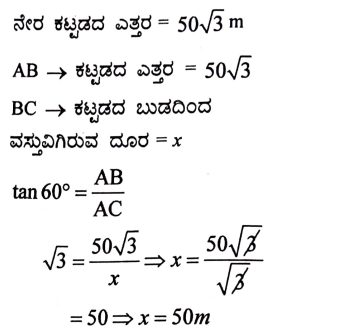
ಅಥವಾ
ಒಂದು ಜಮೀನಿನ ಎರಡೂ ಕಡೆ 50 ಮೀಟರ್ ಮತ್ತು 40√3 ಎತ್ತರವಿರುವ ಎರಡು ಗಾಳಿಯಂತ್ರಗಳಿವೆ. ಆ ಎರಡೂ ಗಾಳಿಯಂತ್ರಗಳ ನಡುವೆ ನಿಂತಿರುವ ಒಬ್ಬ ವ್ಯಕ್ತಿಯು ಅವುಗಳ ತುದಿಯನ್ನು ವೀಕ್ಷಿಸಿದಾಗ ಉಂಟಾದ ಉನ್ನತ ಕೋನವು 45° ಮತ್ತು 30° ಆಗಿರುತ್ತದೆ. ಹಾಗಾದರೆ ಈ ಗಾಳಿಯಂತ್ರಗಳ ನಡುವಿನ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
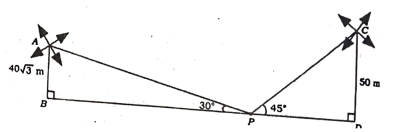
ಉತ್ತರ:

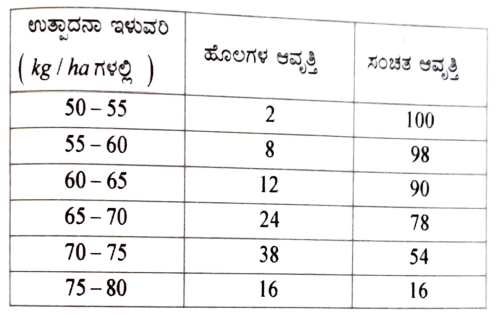
35. ಒಂದು ಗ್ರಾಮದ 100 ಹೊಲಗಳಲ್ಲಿ ಪ್ರತಿ ಹೆಕ್ಟೇರ್ಗೆ ಉತ್ಪಾದಿಸುವ ಗೋಧಿಯ ಇಳುವರಿಯನ್ನು ಕೆಳಗಿನ ಕೋಷ್ಟಕವು ನೀಡುತ್ತಿದೆ:
| ಉತ್ಪಾದನಾ ಇಳುವರಿ ಕೆ.ಜಿ/ ಹೆಕ್ಟೇರ್ ಗಳಲ್ಲಿ | 50 – 55 | 55 – 60 | 60 – 65 | 65 – 70 | 70 – 75 | 75 – 80 |
| ಹೊಲಗಳ ಸಂಖ್ಯೆ | 2 | 8 | 12 | 24 | 38 | 16 |
ಈ ವಿತರಣೆಯನ್ನು ‘ಅಧಿಕ ಇರುವ ವಿಧಾನದ’ ವಿತರಣೆಯಾಗಿ ಬದಲಾಯಿಸಿ, ಇದರ ಓಜೀವ್ ಎಳೆಯಿರಿ.
ಉತ್ತರ:

36. 12 ಸೆಂ.ಮೀ ಪಾದದ ತ್ರಿಜ್ಯ ಹಾಗೂ 20 ಸೆಂ.ಮೀ ಎತ್ತರ ಇರುವ ಶಂಕುವಿನ ಮೇಲ್ಬಾಗದಿಂದ ಪಾದದ ತ್ರಿಜ್ಯ 3 ಸೆಂ.ಮೀ ಇರುವಂತೆ ಒಂದು ಸಣ್ಣ ಶಂಕುವನ್ನು ಕತ್ತರಿಸಿ ತೆಗೆಯಲಾಗಿದೆ. ಹೇಗೆ ಉಂಟಾದ ಶಂಕುವಿನ ಭಿನ್ನಕದ ಫಲಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
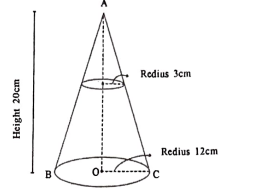
ಉತ್ತರ:

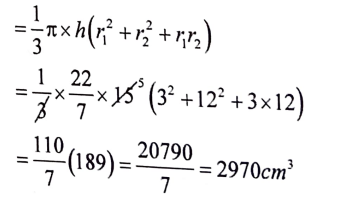
ಅಥವಾ
ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಸಿಲಿಂಡರಿನ ಎರಡೂ ಬದಿಗಳಲ್ಲಿ ಸಮತ್ರಿಜ್ಯವಿರುವ ಅರ್ಧಗೋಳಗಳನ್ನು ಜೋಡಿಸಿರುವ ಆಕಾರದಲ್ಲಿ ಒಂದು ಹಾಲಿನ ಟ್ಯಾಂಕನ್ನು ನಿರ್ಮಿಸಲಾಗಿದೆ. ಈ ಟ್ಯಾಂಕ್ನ ಒಟ್ಟು ಎತ್ತರ 6 ಮೀಟರ್ ಮತ್ತು ತ್ರಿಜ್ಯ 1 ಮೀಟರ್ ಆಗಿದ್ದರೆ. ಈ ಟ್ಯಾಂಕಿನಲ್ಲಿ ತುಂಬಬಹುದಾದ ಹಾಲಿನ ಗರಿಷ್ಠ ಪ್ರಮಾಣವನ್ನು ಲೀಟರ್ ಗಳಲ್ಲಿ ಕಂಡುಹಿಡಿಯಿರಿ. π = 22/7 )
ಉತ್ತರ:
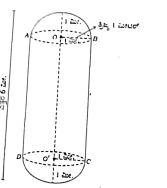
ತ್ರಿಜ್ಯr = 1m ಸಿಲಿಂಡರ್ನ ಎತ್ತರ (h) 6-2=4m
ಹಾಲಿನ ಟ್ಯಾಂಕಿನ ಘನಫಲ = 2 x ಅರ್ಧಗೋಳದ ಘನಫಲ + ಸಿಲಿಂಡರ್ನ ಘನಫಲ
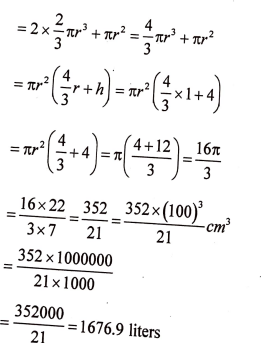
V. ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಉತ್ತರಿಸಿ.
37. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ 4ನೇ ಮತ್ತು 8ನೇ ಪದಗಳ ಮೊತ್ತ 24 ಹಾಗೂ 6ನೇ ಮತ್ತು 10ನೇ ಪದಗಳ ಮೊತ್ತವು 44 ಆದರೆ ಆ ಶ್ರೇಢಿಯ ಮೊದಲ ಮೂರು ಪದಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (4)
ಉತ್ತರ:
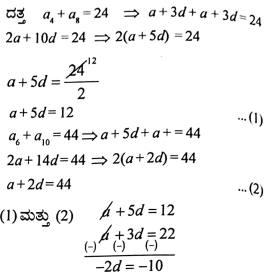
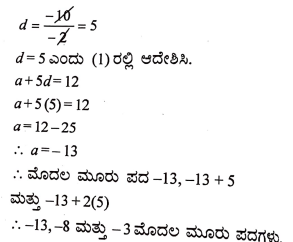
38.”ಒಂದು ಲಂಬಕೋನ ತ್ರಿಭುಜದಲ್ಲಿ ವಿಕರ್ಣದ ಮೇಲಿನ ವರ್ಗವು ಉಳಿದೆರಡು ಬಾಹುಗಳ ಮೇಲಿನ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತವೆ” ಎಂದು ಸಾಧಿಸಿ. (4)
ಉತ್ತರ:
ದತ್ತ.: △ABC ಯು ಒಂದು ಲಂಬಕೋನ ತ್ರಿಭುಜವಾಗಿದ್ದು B ಯು ಲಂಬಕೋನವಾಗಿದೆ.
ಸಾಧನೀಯ: AC2=AB2+BC2
ರಚನೆ: BD ⊥ AC
ಸಾಧನೆ : △ADB ಮತ್ತು AABC ಯಲ್ಲಿ


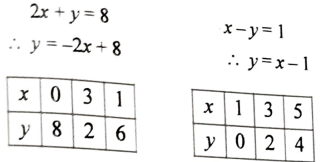
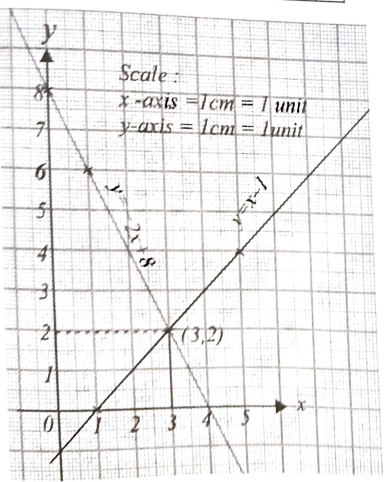
39. ನಕ್ಷೆಯ ಕ್ರಮದಿಂದ ಬಿಡಿಸಿ 2x + y = 8 (4)
ಉತ್ತರ:
40. A ಮತ್ತು B ಎಂಬ ಇಬ್ಬರು ವಿದ್ಯಾರ್ಥಿಗಳ ವಯಸ್ಸು ಕ್ರಮವಾಗಿ 19 ವರ್ಷಗಳು ಮತ್ತು 15 ವರ್ಷಗಳಾಗಿದೆ. ಎಷ್ಟು ವರ್ಷಗಳ ನಂತರ ಇವರಿಬ್ಬರ ವಯಸ್ಸುಗಳ ಗುಣಲಬ್ಧವು 480 ಆಗುತ್ತದೆ ಎಂದು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
A ಮತ್ತು B ಯ ವಯಸ್ಸು 15 ಮತ್ತು 19
ಕೆಲವು ವರ್ಷಗಳ ನಂತರ ವಯಸ್ಸಿನ ಗುಣಲಬ್ಧ = 480
(x + 15)(x + 19) – 480
x2 + 34x – 480 + 285 = 0
x2 + 39x – 5x – 195 = 0
(x – 5)(x + 39) = 0
x=5 ಅಥವಾ x = – 39
-39 ಸಾಧ್ಯವಿಲ್ಲ
ಆದ್ದರಿಂದ 5 ವರ್ಷಗಳ ನಂತರ A ಮತ್ತು B ವಯಸ್ಸಿನ ಗುಣಲಬ್ಧ 480
ಅಥವಾ
(b – c) x2 + (c – a) x + (a – b) = 0 ಸಮೀಕರಣದ ಮೂಲಗಳು ಸಮನಾಗಿದ್ದರೆ 2b = a + c ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ: