10ನೇ ತರಗತಿ ಗಣಿತ ವಾರ್ಷಿಕ ಪರೀಕ್ಷಾ ಪ್ರಶ್ನೆಪತ್ರಿಕೆ ಮಾರ್ಚ್ – 2021, SSLC Annual Exam Question Paper 2021 (ಉತ್ತರಸಹಿತ) SSLC Annual Exam Question Paper 2021 10th standard Annual Exam Question Paper 2021 10ನೇ ತರಗತಿ ಗಣಿತ ವಾರ್ಷಿಕ ಪರೀಕ್ಷಾ ಪ್ರಶ್ನೆಪತ್ರಿಕೆ pdf SSLC Annual Exam Question Paper 2021 pdf kannada medium karnataka sslc question papers with answers pdf download sslc previous year question papers with answers pdf download 10th 5 year question paper kseab karnataka gov in question paper pdf kseab.karnataka.gov.in question paper answer key kseeb key answers

SSLC Supplementary Exam Question Paper 2021
ಈ ಕೆಳಗಿನ ಪ್ರತಿಯೊಂದು ಪ್ರಶ್ನೆಗಳಿಗೆ / ಅಪೂರ್ಣ ಹೇಳಿಕೆಗಳಿಗೆ ನಾಲ್ಕು ಆಯ್ಕೆಗಳನ್ನು ನೀಡಲಾಗಿದೆ. ಅವುಗಳಲ್ಲಿ ಸರಿಯಾದ ಉತ್ತರವನ್ನು ಆರಿಸಿ ನಿಮಗೆ ನೀಡಿರುವ ಉತ್ತರಪತ್ರಿಕೆ ಓ.ಎಂ.ಆರ್. (OMR) ನಲ್ಲಿ ಸರಿಯಾದ ಆಯ್ಕೆಯನ್ನು ಕಪ್ಪು/ನೀಲಿ ಬಾಲ್ ಪಾಯಿಂಟ್ ಪೆನ್ನಿಂದ ಶೇಡ್ ಮಾಡಿರಿ. 40 x 1 = 40
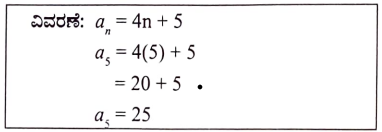
1. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ nನೇ ಪದ an = 4n + 5 ಆದಾಗ, ಅದರ 5ನೇ ಪದವು
(a) 20 (b) 14
(c) 25 (d) 24
ಉತ್ತರ:
(d) 24
2. 5x2 = 2 (2x + 3) ವರ್ಗಸಮೀಕರಣವನ್ನು ಆದರ್ಶರೂಪದಲ್ಲಿ ಬರೆದಾಗ, ದೊರಕುವ ಸ್ಥಿರಾಂಕ
(a) 5 (b) 6
(c) 4 (d) -6
ಉತ್ತರ:
(d) -6
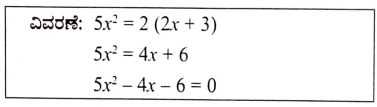
3. x – 2y = 0 ಮತ್ತು 3x + 4y – 20 = 0 ಸಮೀಕರಣಗಳು
(a) ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ
(b) ಐಕ್ಯಗೊಳ್ಳುತ್ತವೆ
(c) ಸಮಾಂತರವಾಗಿರುತ್ತವೆ
(d) ಪರಸ್ಪರ ಲಂಬವಾಗಿರುತ್ತವೆ
ಉತ್ತರ:
(2) ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ
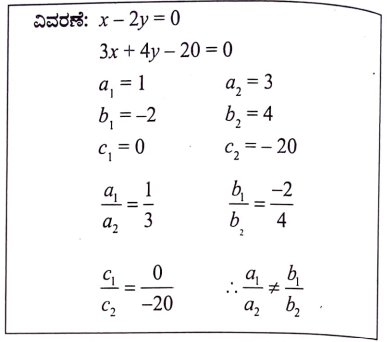
4. ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವ ನಕ್ಷೆಯಲ್ಲಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು
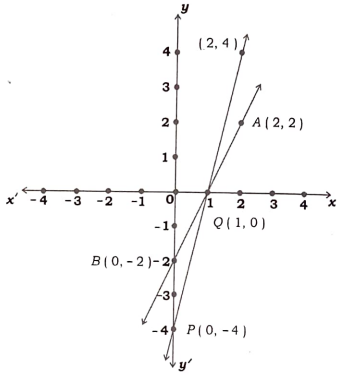
(a) x + y =1 ಮತ್ತು 2x – y = 1
(b) 2x + y =2 ಮತ್ತು x + y = 2
(c) 2x – y = 2 ಮತ್ತು 4x – y = 4
(d) y – x = 0 ಮತ್ತು x – y = 1
ಉತ್ತರ:
(c) 2x – y = 2 ಮತ್ತು 4x – y = 4

5. a1x+b1y+c1=0 ಮತ್ತು a2x+b2y+c2=0 ರೇಖಾತ್ಮಕ ಜೋಡಿ ರೇಖೆಗಳು ಸಮಾಂತರವಾದರೆ ಅವುಗಳ ಸಹಗುಣಗಳ ಸರಿಯಾದ ಸಂಬಂಧವು
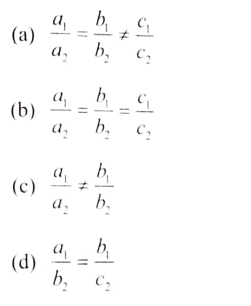
ಉತ್ತರ:
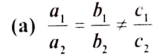
6. 2x + 3y + 7 = 0 ಮತ್ತು ax + by + 14 = 0 ರೇಖೆಗಳ ಜೋಡಿಯು ಪರಸ್ಪರ ಐಕ್ಯಗೊಳ್ಳುವ ರೇಖೆಗಳಾದರೆ, ‘a’ ಮತ್ತು ‘b’ ಬೆಲೆಗಳು ಕ್ರಮವಾಗಿ
(a) 2 ಮತ್ತು 3 (b) 3 ಮತ್ತು 2
(c) 4 ಮತ್ತು 6 (d) 1 ಮತ್ತು 2
ಉತ್ತರ:
(c) 4 ಮತ್ತು 6

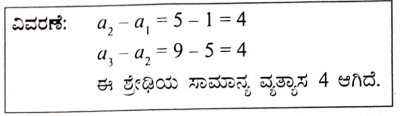
7. ಈ ಕೆಳಗಿನವುಗಳಲ್ಲಿ ಯಾವುದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಾಗಿದೆ ?
(a) 1,-1,-2,……
(b) 1,5,9,……
(c) 2,-2,2,-2…..
(d) 1, 2, 4, 8,…….
ಉತ್ತರ:
(b) 1,5,9,……
8. 3,-1, 1, 3,….. ಸಮಾಂತರ ಶೇಢಿಯ 11 ಪದವು
(a) 23 (b)-23
(c)-17 (d) 17
ಉತ್ತರ:
(d) 17
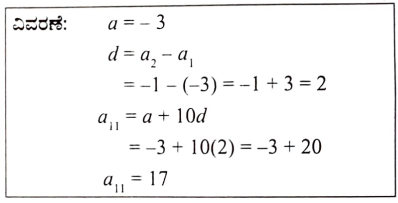
9. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ 10 ಪದಗಳ ಮೊತ್ತವು 155 ಆಗಿದೆ ಮತ್ತು ಅದೇ ಶ್ರೇಢಿಯ ಮೊದಲ 9 ಪದಗಳ ಮೊತ್ತವು 126 ಆದಾಗ ಶ್ರೇಢಿಯ 10ನೇ ಪದವು
(a) 27 (b) 126
(c) 29 (d) 25
ಉತ್ತರ:
(c) 29
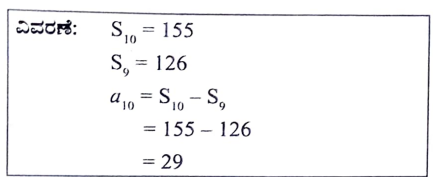
10. 2x2 + ax + 6 = 0 ಸಮೀಕರಣದ ಒಂದು ಮೂಲವು 2 ಆದಾಗ, ‘a’ ಯ ಬೆಲೆ

ಉತ್ತರ:
(c) -7

11. px2 + qx + r = 0 ವರ್ಗ ಸಮೀಕರಣದ ಶೋಧಕವು
(a) q2 – 4pr (b) q2 + 4pr
(c) p2 – 4pr (d) p2 + 4qr
ಉತ್ತರ:
(a) q2 – 4pr
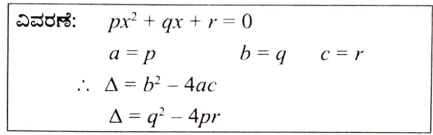
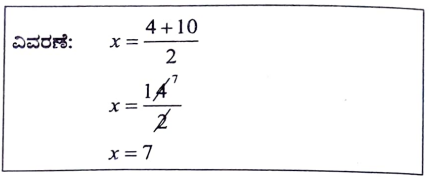
12. 4, x, 10 ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿದ್ದರೆ x’ ನ ಬೆಲೆಯು
(a) 14 (b) -6
(c)-7 (d) 7
ಉತ್ತರ:
(d) 7
13. ax2 + bx + c = 0 ವರ್ಗಸಮೀಕರಣದ ಮೂಲಗಳು
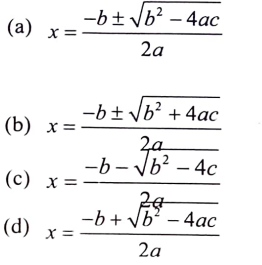
ಉತ್ತರ:
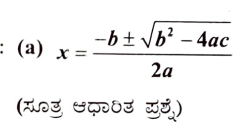
14. (x – 3)(x + 2) = 0 ಸಮೀಕರಣದ ಮೂಲಗಳು
(a) -3,2 (b) 3,-2
(c) -3,-2 (d) 3,2
ಉತ್ತರ:
(b) 3,-2
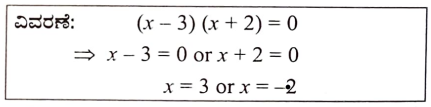
15. ಎರಡು ಅನುಕ್ರಮ ಪೂರ್ಣಾಂಕಗಳ ಮೊತ್ತವು 27 ಆದರೆ ಆ ಪೂರ್ಣಾಂಕಗಳು
(a) 7 ಮತ್ತು 20 (b) 13 ಮತ್ತು 14
(c) 1 ಮತ್ತು 26 (d) – 13 ಮತ್ತು -14
ಉತ್ತರ:
(b) 13 ಮತ್ತು 14

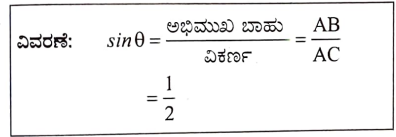
16. ಕೊಟ್ಟಿರುವ ಚಿತ್ರದಲ್ಲಿ sin θ ದ ಬೆಲೆಯು
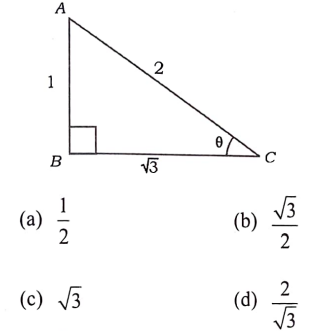
ಉತ್ತರ:
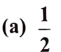
17. ( sin 300 + cos 600 – tan 450 ) ಯ ಬೆಲೆ
(a) 2 (b) 1
(c) 2 (d) 0
ಉತ್ತರ:
(d) 0
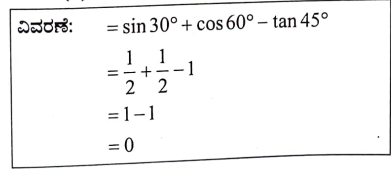
18. 3 + sec2 θ ಇದಕ್ಕೆ ಸಮನಾದುದು
(a) 4 + tan2θ (b) 4 + cot2θ
(c) 2 + cot2θ (d) 3 + cot2θ
ಉತ್ತರ:
(a) 4 + tan2θ

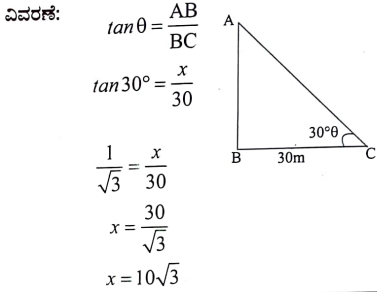
19. ಗೋಪುರದ ಪಾದದಿಂದ 30 ಮೀ. ದೂರದ ನೆಲದ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಿನಿಂದ ಗೋಪುರದ ತುದಿಯನ್ನು ವೀಕ್ಷಿಸಿದಾಗ ಉಂಟಾಗುವ ಉನ್ನತ ಕೋನವು 30° ಆದರೆ, ಆ ಗೋಪುರದ ಎತ್ತರವು
(a) 10 m (b) 30 m
(c) 10√3 m (d) 30√3 m
ಉತ್ತರ:
(c) 10√3 m
20. (sinθ x cosecθ) ದ ಬೆಲೆಯು

ಉತ್ತರ:
(b) 1
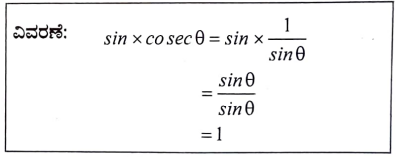
21. A (x1, y1) ಮತ್ತು B (x2, y2) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡದ ಮಧ್ಯಬಿಂದುವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರ

ಉತ್ತರ:
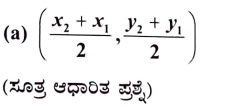
22. (x1, y1) ಮತ್ತು (x2, y2) ಬಿಂದುಗಳಿರುವ ದೂರವು
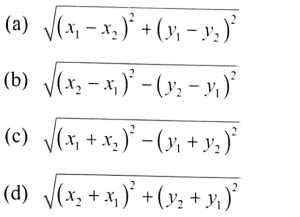
ಉತ್ತರ:
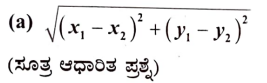
23. ದತ್ತ ಪ್ರಾಪ್ತಾಂಕಗಳಲ್ಲಿ ಅತಿ ಹೆಚ್ಚು ಸಲ ಪುನರಾವರ್ತಿಸುವ ಸಂಖ್ಯೆಯ ಮೌಲ್ಯವು ಪ್ರಾಪ್ತಾಂಕಗಳ
(a) ಸರಾಸರಿಯಾಗಿದೆ
(b) ಬಹುಲಕ ಆಗಿದೆ
(c) ಮಾಧ್ಯಾಂಕವಾಗಿದೆ
(d) ವ್ಯಾಪ್ತಿ ಆಗಿದೆ
ಉತ್ತರ:
(b) ಬಹುಲಕ ಆಗಿದೆ
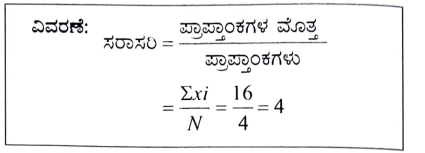
24. ಈ ಕೆಳಗಿನ ದತ್ತಾಂಶಗಳ ‘ಸರಾಸರಿ’ಯು

(a) 16 (b) 5
(c) 1.6 (d) 4
ಉತ್ತರ:
(d) 4
25. ಕೆಲವು ದತ್ತಾಂಶಗಳ ‘ಸರಾಸರಿ’ ಮತ್ತು ‘ಬಹುಲಕ’ ಹಾಗೂ ಮಧ್ಯಾಂಕಗಳ ಸಂಬಂಧವು
(a) 3 ಮಧ್ಯಾಂಕ = 2 ಸರಾಸರಿ + ಬಹುಲಕ
(b) 3 ಸರಾಸರಿ 2 ಮಧ್ಯಾಂಕ + ಬಹುಲಕ
(c) ಸರಾಸರಿ = 3 ಮಧ್ಯಾಂಕ + ಬಹುಲಕ
(d) ಮಧ್ಯಾಂಕ = 3 ಸರಾಸರಿ + ಮಧ್ಯಾಂಕ
ಉತ್ತರ:
(a) 3 ಮಧ್ಯಾಂಕ = 2 ಸರಾಸರಿ + ಬಹುಲಕ
26. ಮೇಣದಿಂದ ಮಾಡಲ್ಪಟ್ಟ ಒಂದು ಸಿಲಿಂಡರನ್ನು ಕರಗಿಸಿ ಅದನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಒಂದು ಗೋಳದ ಆಕಾರಕ್ಕೆ ಬದಲಾಯಿಸಿದಾಗ ದೊರಕುವ ಗೋಳದ ಘನಫಲವು
(3) ಸಿಲಿಂಡರ್ನ ಘನಫಲದ ಎರಡರಷ್ಟಾಗುತ್ತದೆ
(b) ಸಿಲಿಂಡರ್ ಘನಫಲದ ಅರ್ದದಷ್ಟಾಗುತ್ತದೆ
(c) ಸಿಲಿಂಡರ್ನ ಘನಫಲದ ಮೂರರಷ್ಟಾಗುತ್ತದೆ
(d) ಸಿಲಿಂಡರ್ನ ಘನಫಲದಷ್ಟೇ ಇರುತ್ತದೆ
ಉತ್ತರ:
(d) ಸಿಲಿಂಡರ್ನ ಘನಫಲದಷ್ಟೇ ಇರುತ್ತದೆ
ವಿವರಣೆ: ಒಂದು ಘನವನ್ನು ಯಾವುದೇ ಆಕಾರಕ್ಕೆ ಬದಲಾಯಿಸಿದರೆ ಅದರ ಘನಫಲ ಬದಲಾಗುವುದಿಲ್ಲ.
27. ವರ್ಗಾಂತರ ಮಧ್ಯಬಿಂದು (ಅಂಕ) ವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರ
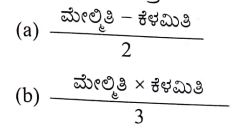
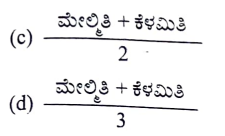
ಉತ್ತರ:
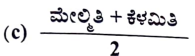
28. △ABC ಯಲ್ಲಿ XY ∥ BC
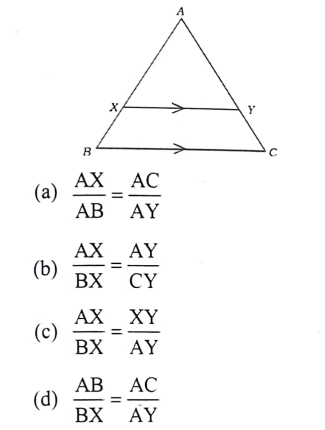
ಉತ್ತರ:
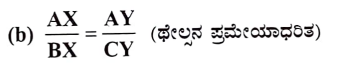
29. ಕೊಟ್ಟಿರುವ ಎರಡು ತ್ರಿಭುಜಗಳನ್ನು ಗಮನಿಸಿ, ನಂತರ DF ನ ಆಳತೆಯನ್ನು ಗುರುತಿಸಿ
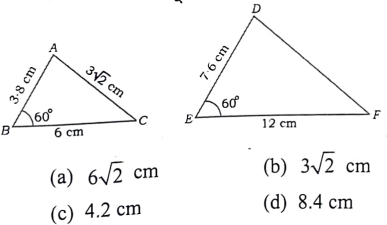
ಉತ್ತರ:

30. △ABC ∼ △PQR, △ABC ವಿಸ್ತೀರ್ಣ = 64cm² ಮತ್ತು △PQR ವಿಸ್ತೀರ್ಣ 100cm² ಆಗಿದೆ. AB = 8cm ಆದಾಗ PQನ ಉದ್ದವು
(a) 12cm (b) 15cm
(c) 10cm (d) 8cm
ಉತ್ತರ:
(c). 10cm

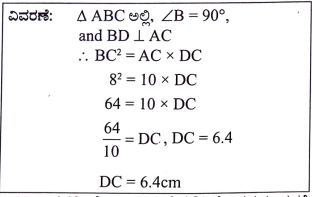
31. △ABC ಯಲ್ಲಿ, ∠B = 90° ಮತ್ತು BD ⊥ AC. AB = 6cm BC = 8cm ಆದಾಗ CD ಯ ಉದ್ದವು
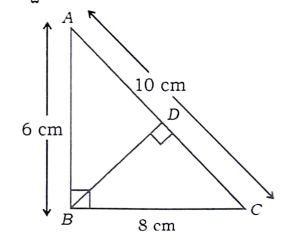
(a) 10 cm (b) 6.4 cm
(c) 4.8 cm (d) 3.6 cm
ಉತ್ತರ:
(b) 6.4 cm
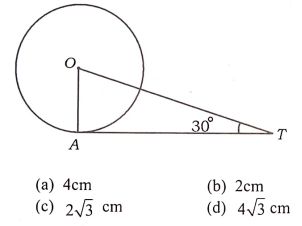
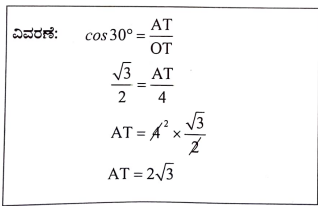
32. ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ‘O’ ಕೇಂದ್ರವುಳ್ಳ ವೃತ್ತಕ್ಕೆ A ಬಿಂದುವಿನಲ್ಲಿ AT ಸ್ಪರ್ಶಕವನ್ನು ಎಳೆಯಲಾಗಿದೆ. ∠OTA =300 ಮತ್ತು OT = 4 cm ಆದರೆ, AT ಯ ಉದ್ದ.
ಉತ್ತರ:
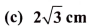
33. ಚಿತ್ರದಲ್ಲಿ PA, PBC ಮತ್ತು CD ಗಳು ‘O’ ಕೇಂದ್ರವುಳ್ಳ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳಾಗಿವೆ. PC = 8 cm ಮತ್ತು AP = 5 cm ಆದಾಗ, CD ಸ್ಪರ್ಶಕದ ಉದ್ದವು.
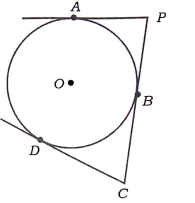
(a) 5 cm (b) 3 cm
(c) 8 cm (d) 13 cm
ಉತ್ತರ:
b) 3 cm

34. ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳಲ್ಲಿ ‘ತಪ್ಪು ಹೇಳಿಕೆಯನ್ನು’ ಗುರುತಿಸಿ.
(೩) ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕವು ವೃತ್ತವನ್ನು ಒಂದೇ ಬಿಂದುವಿನಲ್ಲಿ ಸ್ಪರ್ಶಿಸುತ್ತದೆ
(b) ವೃತ್ತಕ್ಕೆ ಒಂದು ಸರಳ ರೇಖೆಯನ್ನು ಎಳೆದಾಗ ಅದು ಯಾವಾಗಲು ವೃತ್ತದ ಒಂದೇ ಒಂದು ಬಿಂದುವಿನಿಂದ ಹಾದು ಹೋಗುತ್ತದೆ
(d) ವೃತ್ತಕ್ಕೆ ಒಂದು ಸರಳ ರೇಖೆಯನ್ನು ಎಳೆದಾಗ ಅದು ವೃತ್ತವನ್ನು ಸ್ಪರ್ಶಿಸುವ ಬಿಂದುವನ್ನು ಸ್ಪರ್ಶಬಿಂದು ಎಂದು ಕರೆಯುತ್ತೇವೆ
(d) ಸ್ಪರ್ಶಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ತ್ರಿಜ್ಯವು ಸ್ಪರ್ಶರೇಖೆಗೆ ಲಂಬವಾಗಿರುತ್ತದೆ
ಉತ್ತರ:
(b) ವೃತ್ತಕ್ಕೆ ಒಂದು ಸರಳ ರೇಖೆಯನ್ನು ಎಳೆದಾಗ ಅದು ಯಾವಾಗಲು ವೃತ್ತದ ಒಂದೇ ಒಂದು ಬಿಂದುವಿನಿಂದ ಹಾದು ಹೋಗುತ್ತದೆ.
ವಿವರಣೆ: ಸರಳ ರೇಖೆಯು ವೃತ್ತವನ್ನು ಕನಿಷ್ಠ ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಗರಿಷ್ಠ ಎರಡು ಬಿಂದುವಿನ ಮೂಲಕ ಹಾದು ಹೋಗುತ್ತದೆ.
35. ದತ್ತ ವೃತ್ತಕ್ಕೆ ಅದರ ಹೊರಗಿನ ಬಿಂದು ‘T’ಯಿಂದ ಎರಡು ಸ್ಪರ್ಶಕಗಳನ್ನು ರಚಿಸುವಾಗ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವ ರಚನೆಯ ಹಂತದ ಮುಂದಿನ ಹಂತವನ್ನು ಗುರುತಿಸಿ.
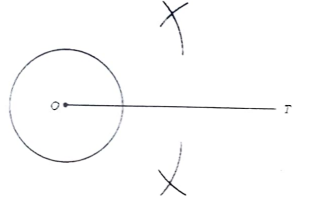
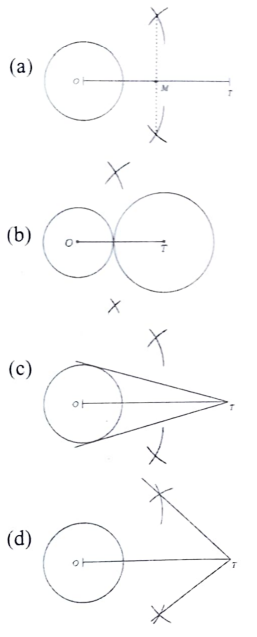
ಉತ್ತರ:
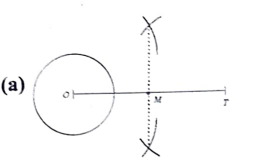
36. ಒಂದು ಗೋಳದ ಮೇಲೆ ವಿಸ್ತೀರ್ಣ 616cm² ಆಗಿದೆ. ಅದೇ ಗೋಳದ ತ್ರಿಜ್ಯವು
(a) 49 cm (b) 14 cm
(c) 21 cm (d) 7 cm
ಉತ್ತರ:
(d) 7 cm

37. ಕೊಟ್ಟಿರುವ ಶಂಕುವಿನ ಘನಫಲ ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರವು
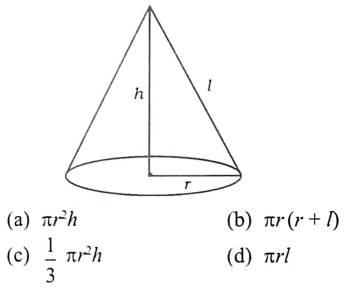
ಉತ್ತರ:
38. ಎರಡು ಪಾದಗಳಲ್ಲಿ ಒಂದು ಪಾದ ತೆರೆಯಲ್ಪಟ್ಟಿರುವ ನೇರ ಸಿಲಿಂಡರಿನ ಪಾದದ ತ್ರಿಜ್ಯ r cm ಮತ್ತು ಅದರ ಎತ್ತರ h cm ಆದಾಗ ಸಿಲಿಂಡರಿನ ಪೂರ್ಣ ಮೇಲೆ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರ
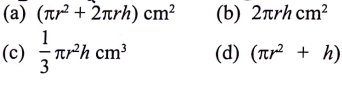
ಉತ್ತರ:
39. ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವ ಬಿನ್ನಕ ಶಂಕುವಿನ ವಕ್ರಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರವು
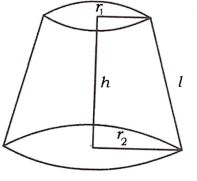
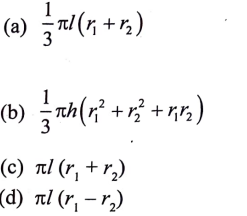
ಉತ್ತರ:
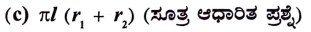
40. ಒಂದು ಘನ ಅರ್ಧಗೋಳದ ಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವು 462 cm2 ಆಗಿದೆ ಮತ್ತು ಅದರ ವಕ್ರಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವು 308 cm2 ಆದಾಗ ಅರ್ಧಗೋಳದ ಪಾದದ ವಿಸ್ತೀರ್ಣವು
(a) 308 cm2 (b) 231 cm2
(c) 154 cm2 (d) 1078 cm2
ಉತ್ತರ:
(c) 154 cm2
ವಿವರಣೆ: ಅರ್ಧಗೋಳದ ಪಾದದ ವಿಸ್ತೀರ್ಣ = ಅರ್ಧಗೋಳದ ಪೂ.ಮೇ.ವಿ – ಪಾ.ಮೇ
∴ ವಿಸ್ತೀರ್ಣ = 462 – 308 = 154 cm2
