10th Standard Sambhavaneeyate Maths Notes Question Answer Guide Extract Mcq Pdf Download Kannada Medium Karnataka State Syllabus 2025 ಸಂಭವನೀಯತೆ ನೋಟ್ಸ್ 10th sambhavaniyate maths notes sambavaniyate notes in kannada sambhavaniyate 10th kannada notes 10ನೇ ತರಗತಿ ಗಣಿತ ಸಂಭವನೀಯತೆ ನೋಟ್ಸ್ Pdf ಪ್ರಶ್ನೋತ್ತರಗಳು kseeb solutions for class 10 maths chapter 14 notes in kannada medium
ಘಟಕ 14 – ಸಂಭವನೀಯತೆ
10ನೇ ತರಗತಿ ಗಣಿತ ಸಂಭವನೀಯತೆ ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು
ಅಭ್ಯಾಸ 14.1
1. ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳನ್ನು ಪೂರ್ತಿಗೊಳಿಸಿ.
(i) ಒಂದು ಘಟನೆ E ಯ ಸಂಭವನೀಯತೆ + ‘E ಅಲ್ಲದ’ ಘಟನೆಯ ಸಂಭವನೀಯತೆ = _________________
(ii) ಸಂಭವಿಸಲು ಅಸಾಧ್ಯವಾದ ಘಟನೆಯ ಸಂಭವನೀಯತೆಯು ____________ ಇಂತಹ ಘಟನೆಯನ್ನು ____________ ಎನ್ನುತ್ತಾರೆ.
(iii) ಖಚಿತವಾಗಿ ಸಂಭವಿಸುವ ಒಂದು ಘಟನೆಯ ಸಂಭವನೀಯತೆಯು _____________ ಇಂತಹ ಘಟನೆಯನ್ನು ____________ ಎನ್ನುತ್ತಾರೆ.
(iv) ಒಂದು ಪ್ರಯೋಗದ ಎಲ್ಲಾ ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಸಂಭವನೀಯತೆಗಳ ಮೊತ್ತವು ______________
(v) ಒಂದು ಘಟನೆಯ ಸಂಭವನೀಯತೆಯು ___________ ಗಿಂತ ದೊಡ್ಡದು ಅಥವಾ ಸಮ ಮತ್ತು ____________ ಕ್ಕಿಂತ ಚಿಕ್ಕದು ಅಥವಾ ಸಮನಾಗಿರುತ್ತದೆ.
ಉತ್ತರ:
(i) 1
(ii) ಅಸಂಭವ ಘಟನೆ (ಅಸಾಧ್ಯ ಘಟನೆ)
(iii) ಖಚಿತ ಅಥವಾ ನಿಶ್ಚಿತ ಘಟನೆ
(iv) 1
(v) 0, 1
2. ಕೆಳಗಿನ ಯಾವ ಪ್ರಯೋಗಗಳು ಸಮಾನ ಫಲಿತಗಳನ್ನು ಹೊಂದಿವೆ? ವಿವರಿಸಿ
(i) ಒಬ್ಬ ಚಾಲಕನು ಕಾರನ್ನು ಸ್ಟಾರ್ಟ್ ಮಾಡಲು ಪ್ರಯತ್ನಿಸುತ್ತಾನೆ. ಕಾರು ಸ್ಟಾರ್ಟ್ ಆಗುವುದು ಅಥವಾ ಸ್ಟಾರ್ಟ್ ಆಗದಿರುವುದು.
(ii) ಒಬ್ಬ ಆಟಗಾರ ಬಾಸ್ಕೆಟ್ ಬಾಲ್ನ್ನು ಗುರಿಯತ್ತ ಎಸೆಯಲು ಪ್ರಯತ್ನಿಸುತ್ತಾನೆ ಅವನ/ಅವಳ ಗುರಿ ಮುಟ್ಟುವುದು ಅಥವಾ ಗುರಿಮುಟ್ಟದೇ ಇರುವುದು
(iii) ಸರಿ – ತಪ್ಪು ಉತ್ತರವಿರುವ ಪ್ರಶ್ನೆಯನ್ನು ಉತ್ತರಿಸಲು ಪ್ರಯತ್ನಿಸಲಾಗಿದೆ ಉತ್ತರವು ಸರಿ ಅಥವಾ ತಪ್ಪು ಆಗಿರುವುದು.
(iv) ಒಂದು ಮಗುವು ಜನಿಸಿದೆ ಇದು ಒಂದು ಗಂಡು ಅಥವಾ ಒಂದು ಹೆಣ್ಣು ಆಗಿರುವುದು.
ಉತ್ತರ:
(iii) ಮತ್ತು (iv) ಈ ಪ್ರಯೋಗಗಳು ಸಮಾನ ಸಾಧ್ಯತೆಯ ಫಲಿತಗಳನ್ನು ಹೊಂದಿವೆ.
3. ಒಂದು ಫುಟ್ ಬಾಲ್ ಆಟದ ಆರಂಭದಲ್ಲಿ, ಯಾವ ತಂಡವು ಮೊದಲು ಚೆಂಡನ್ನು ಪಡೆಯಬೇಕು ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸಲು ನಾಣ್ಯವನ್ನು ಚಿಮ್ಮುವುದು ಒಂದು ಉತ್ತಮ ವಿಧಾನವಾಗಿದೆ ಎಂದು ಏಕೆ ಪರಿಗಣಿಸಲಾಗಿದೆ?
ಉತ್ತರ:
ನಾವು ಒಂದು ನಾಣ್ಯವನ್ನು ಚಿಮ್ಮಿದಾಗ ಶಿರವನ್ನು ಮತ್ತು ಪುಚ್ಛವನ್ನು ಪಡೆಯುವ ಫಲಿತಗಳು ಸಮಾನ ಸಾಧ್ಯತೆಯದಾಗಿವೆ. ಆದ್ದರಿಂದ ಒಂದು ನಾಣ್ಯದ ಚಿಮ್ಮುವಿಕೆಯ ಫಲಿತಾಂಶವು ಪೂರ್ಣವಾಗಿ ಊಹಿಸಲು ಅಸಾಧ್ಯವಾದುದಾಗಿದೆ.
4. ಕೆಳಗಿನವುಗಳಲ್ಲಿ ಯಾವುದು ಒಂದು ಘಟನೆಯ ಸಂಭವನೀಯತೆ ಆಗಿರಲು ಸಾಧ್ಯವಿಲ್ಲ.
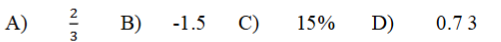
ಉತ್ತರ:
(B) – 1. 5
5. P(E) = 0.05 ಆದರೆ, ́E ಅಲ್ಲದʼ ಘಟನೆಯ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:
P(E) = 0.05
P(E) + P(E) = 1
P(E) = 1 – P(E)
= 1-0.05 = 0.95
6. ಒಂದು ಚೀಲವು ನಿಂಬೆ ಪರಿಮಳದ ಕ್ಯಾಂಡಿಗಳನ್ನು ಮಾತ್ರ ಒಳಗೊಂಡಿದೆ. ಮಾಲಿನಿಯು ಚೀಲದೊಳಗೆ ನೋಡದೆ ಒಂದು ಕ್ಯಾಂಡಿಯನ್ನು ಹೊರತೆಗೆಯುತ್ತಾಳೆ. ಅವಳು ಹೊರತೆಗೆಯುವ ಕ್ಯಾಂಡಿಯು
(i) ಒಂದು ಕಿತ್ತಳೆ ಪರಿಮಳದ ಕ್ಯಾಂಡಿಯಾಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
(ii) ಒಂದು ನಿಂಬೆ ಪರಿಮಳದ ಕ್ಯಾಂಡಿಯಾಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:
ಒಂದು ಚೀಲವು ನಿಂಬೆ ಕ್ಯಾಂಡಿಗಳನ್ನು ಮಾತ್ರಹೊಂದಿದೆ. ಅತ್ತ ಎಂದು ಊಹಿಸೋಣ.
ಒಟ್ಟು ಕ್ಯಾಂಡಿಗಳು = 10.
(i) ಕಿತ್ತಳೆ ಪರಿಮಳದ ಕ್ಯಾಂಡಿಯನ್ನು ಪಡೆಯಲು ಯತ್ನಿಸಿದ ಘಟನೆಗಳ ಸಂಖ್ಯೆ = 0
∴ ಘಟನೆ Aಗೆ ಅನುಕೂಲಿಸುವ ಪರಿಣ ಸಂಖ್ಯೆ = 0
P(A) = 0/10 = 0
(ii) ನಿಂಬೆ ಪರಿಮಳದ ಕ್ಯಾಂಡಿಯಾ ಪಡೆಯಲು ಯತ್ನಿಸಿದ ಘಟನೆಗಳ ಸಂಖ್ಯೆ = 0 ಪರಿಮಳದ
∴ ಘಟನೆ Bಗೆ ಅನುಕೂಲಿಸುವ ಫಲಿತಗಳ ಸಂಖ್ಯೆ =10
P(B) = 10/10 = 1
7. 3 ಮಕ್ಕಳ ಒಂದು ಗುಂಪಿನಲ್ಲಿ, 2 ಮಕ್ಕಳ ಜನ್ಮದಿನವು ಒಂದೇ ದಿನ ಆಗಿರದ ಸಂಭವನೀಯತೆಯು 0.992 ಎಂದು ನೀಡಿದೆ. 2 ಮಕ್ಕಳ ಜನ್ಮದಿನವು ಒಂದೇ ದಿನ ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:
P(E) = 2 ಮಕ್ಕಳ ಜನ್ಮದಿನವು ಒಂದೇ ದಿನ ಆಗಿರದ ಸಂಭವನೀಯತೆ
∴ P(E) = 0.992
P(E) + P(E) = 1
P(E) = 1 – P(E)
=1-0.992 =0.008
∴ 2 ಮಕ್ಕಳ ಜನ್ಮದಿನವು ಒಂದೇ ದಿನ ಆಗಿರುವ ಸಂಭವನೀಯತೆಯು 0.008
8. ಒಂದು ಚೀಲದಲ್ಲಿ 3 ಕೆಂಪು ಚೆಂಡುಗಳು ಮತ್ತು 5 ಕಪ್ಪು ಚೆಂಡುಗಳಿವೆ. ಚೀಲದಿಂದ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಚೆಂಡನ್ನು ತೆಗೆಯಲಾಗಿದೆ. ತೆಗೆದ ಚೆಂಡು (1) ಕೆಂಪು (ii) ಕೆಂಪು ಅಲ್ಲದ ಚೆಂಡು ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:

9. ಒಂದು ಪೆಟ್ಟಿಗೆಯಲ್ಲಿ 5 ಕೆಂಪು ಗೋಲಿಗಳು. 8 ಬಿಳಿ ಗೋಲಿಗಳು ಮತ್ತು 4 ಹಸಿರು ಗೋಲಿಗಳಿವೆ. ಪೆಟ್ಟಿಗೆಯಿಂದ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಗೋಲಿಯನ್ನು ಹೊರ ತೆಗೆಯಲಾಗಿದೆ. ಹೊರತೆಗೆದ ಗೋಲಿಯು (1) ಕೆಂಪು (ii) ಬಿಳಿ (iii) ಹಸಿರು ಅಲ್ಲದ ಗೋಲಿ ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:

10. ಒಂದು ಗೋಲಕವು (ಹಣದ ಹುಂಡಿ) 50 ಪೈಸೆಯ 100 ನಾಣ್ಯಗಳನ್ನು, ₹1 ರ 50 ನಾಣ್ಯಗಳನ್ನು, ₹2 ಯು 20 ನಾಣ್ಯಗಳನ್ನು ₹5 ರ 10 ನಾಣ್ಯಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಅದನ್ನು ಬೋರಲು ಹಾಕಿದಾಗ ಯಾವುದಾದರೂ ಒಂದು ನಾಣ್ಯ ಹೊರ ಬೀಳುವ ಸಮಾನ ಸಾಧ್ಯತೆಗಳವೆ. ಆ ನಾಣ್ಯವು (i) ಒಂದು 50 ಪೈಸೆ ನಾಣ್ಯವಾಗಿರುವ (ii) ಒಂದು 15 ರ ನಾಣ್ಯ ಆಗಿರದ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:
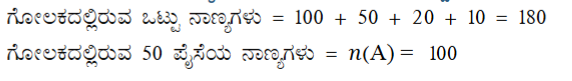
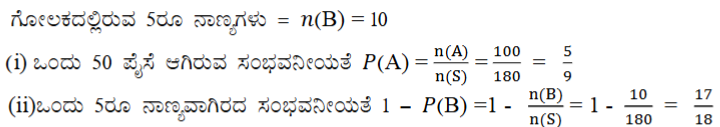
11. ಗೋಪಿಯು ತನ್ನ ಅಕ್ಟೋರಿಯಂ ಗೆ ಒಂದು ಅಂಗಡಿಯಿಂದ ಒಂದು ಮೀನನ್ನು ಖರೀದಿಸುತ್ತಾನೆ. ಅಂಗಡಿಯವನು ಟ್ಯಾಂಕ್ನಲ್ಲಿರುವ 5 ಗಂಡು ಮೀನುಗಳು ಮತ್ತು 8 ಹೆಣ್ಣು ಮೀನುಗಳಿಂದ (ಚಿತ್ರ 14.4 ನ್ನು ನೋಡಿ) ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಮೀನನ್ನು ಹೊರ ತೆಗೆಯುತ್ತಾನೆ. ಹೊರ ತೆಗೆಯುವ ಮೀನು ಗಂಡು ಮೀನು ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:

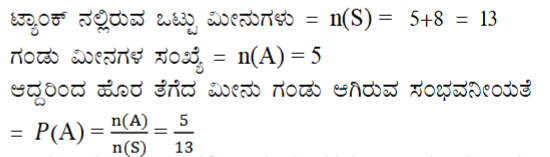
12. ಒಂದು ಅವಕಾಶದ ಆಟದಲ್ಲಿ ಒಂದು ಸೂಚಕವು (ಬಾಣವು) ಚಿತ್ರಾಕಾರವಾಗಿ ತಿರುಗಿ 1, 2, 3, 4, 5, 6, 7, 8 ಈ ಅಂಕಿಗಳಲ್ಲಿ ಯಾವುದಾದರೂ ಒಂದು ಅಂಕಿಯನ್ನು ಸೂಚಿಸುವಂತೆ ನಿಶ್ಚಲವಾಗುತ್ತದೆ ಮತ್ತು ಇವೆಲ್ಲವೂ ಸಮಾನ ಸಾಧ್ಯತೆಗಳನ್ನು ಹೊಂದಿವೆ (ಚಿತ್ರ 14.5 ನ್ನು ನೋಡಿ). ಸೂಚಕವು
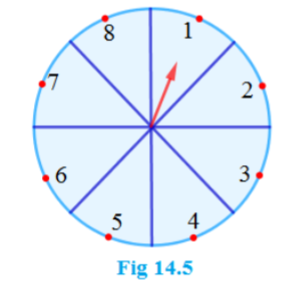
(i) 8 ?
(ii) ಒಂದು ಬೆಸಸಂಖ್ಯೆ
(ii) 2 ಕ್ಕಿಂತ ದೊಡ್ಡದಾದ ಒಂದು ಸಂಖ್ಯೆ
(iv) 9 ಕ್ಕಿಂತ ಚಿಕ್ಕದಾದ ಒಂದು ಸಂಖ್ಯೆಯನ್ನು ಸೂಚಿಸುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:


13. ಒಂದು ದಾಳವನ್ನು ಒಂದು ಸಲ ಎಸೆಯಲಾಗಿದೆ.
(i) ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ
(ii) 2 ಮತ್ತು 6 ರ ನಡುವಿನ ಒಂದು ಸಂಖ್ಯೆ
(iii) 20 ಬೆಸಸಂಖ್ಯೆಯನ್ನು ಪಡೆಯುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:


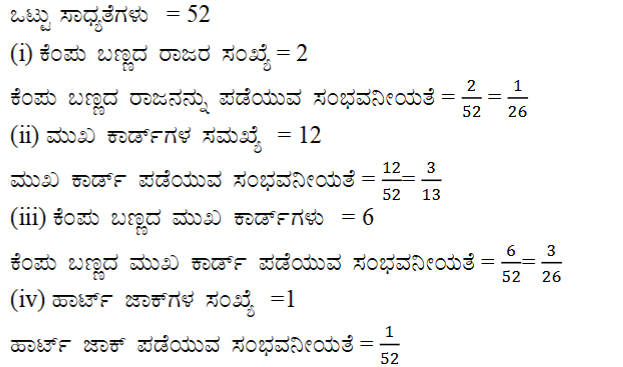
14. ಚೆನ್ನಾಗಿ ಬೆರೆಸಿದ 52 ಕಾರ್ಡ್ಗಳ ಒಂದು ಕಟ್ಟಿನಿಂದ ಒಂದು ಕಾರ್ಡ್ನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ತೆಗೆಯಲಾಗಿದೆ.
(i) ಒಂದು ಕೆಂಪು ರಾಜ
(ii) ಒಂದು ಮುಖ (ಗೌರವಾನ್ವಿತ) ಕಾರ್ಡ್
(iii) ಒಂದು ಕೆಂಪು ಬಣ್ಣದ ಮುಖ (ಗೌರವಾನ್ವಿತ) ಕಾರ್ಡ್
(iv) ಹಾರ್ಟ್ನ ಜ್ಯಾಕ್
(v) ಒಂದು ಸ್ಪೇಡ್
(vi) ಡೈಮಂಡ್ ರಾಣಿ ಪಡೆಯುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

15. ಡೈಮಂಡ್ನ 5 ಕಾರ್ಡ್ ಗಳಾದ, 10, ಜ್ಯಾಕ್, ರಾಣಿ, ರಾಜ ಮತ್ತು ಎಸ್ಗಳನ್ನು ಅವುಗಳ ಮುಖ ಕೆಳಕ್ಕೆ ಇರುವಂತೆ ಚೆನ್ನಾಗಿ ಬೆರೆಸಲಾಗಿದೆ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಕಾರ್ಡ್ ನ್ನು ಆರಿಸಲಾಗಿದೆ.
(i) ಆ ಕಾರ್ಡ್ ರಾಣಿ ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
(ii) ರಾಣಿ ಕಾರ್ಡ್ ನ್ನು ತೆಗೆದು ಪಕ್ಕದಲ್ಲಿರಿಸಿ, ಎರಡನೇ ಕಾರ್ಡ್ನ್ನು ಆರಿಸಿದಾಗ ಅದು (a) ಒಂದು ಏಸ್ (b) ಒಂದು ರಾಣಿ ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:

16. 12 ದೋಷಪೂರಿತ ಪೆನ್ ಗಳು ಆಕಸ್ಮಿಕವಾಗಿ 132 ಉತ್ತಮ ಪೆನ್ ಗಳೊಂದಿಗೆ ಸೇರಿಕೊಂಡಿವೆ. ಒಂದು ಪೆನ್ನನ್ನು ನೋಡಿದ ಕೂಡಲೇ ಅದು ದೋಷಪೂರಿತವೇ? ಅಲ್ಲವೇ? ಎಂಬುದನ್ನು ಹೇಳಲು ಸಾಧ್ಯವಿಲ್ಲ. ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಪೆನ್ನನ್ನು ಗುಂಪಿನಿಂದ ಹೊರ ತೆಗೆಯಲಾಗಿದೆ ಹೊರತೆಗೆದ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

17. (i) 20 ಬಲ್ಬಗಳ ಒಂದು ಗುಂಪಿನಲ್ಲಿ 4 ಬಲ್ಸ್ಗಳು ದೋಷಪೂರಿತವಾಗಿವೆ. ಗುಂಪಿನಿಂದ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಬಲ್ಬನ್ನು ಹೊರತೆಗೆಯಲಾಗಿದೆ. ಅದು ದೋಷಪೂರಿತ ಆಗಿರುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
(ii). (i) ರಲ್ಲಿ ಹೊರ ತೆಗೆದ ಬಲ್ಬ್ ದೋಷಪೂರಿತವಾಗಿರದಿದ್ದರೂ ಸಹ ಅದನ್ನು ಬಲ್ಬ್ ಗಳ ಗುಂಪಿನಿಂದ ಪ್ರತ್ಯೇಕಿಸಿದೆ. ಈಗ ಉಳಿದ ಬಲ್ಬ್ ಗಳಿಂದ ಒಂದು ಬಲ್ಬ್ ನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಹೊರ ತೆಗೆದರೆ ಈ ಬಲ್ಬ್ ದೋಷಪೂರಿತವಾಗಿರದ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:

18. ಒಂದು ಪೆಟ್ಟಿಗೆಯಲ್ಲಿ 1 ರಿಂದ 90 ರರೆಗಿನ ಸಂಖ್ಯೆಗಳು ನಮೂದಾಗಿರುವ 90 ಜಿಲ್ಲೆಗಳಿವೆ. ಪೆಟ್ಟಿಗೆಯಿಂದ ಒಂದು ಬಿಲ್ಲೆಯನ್ನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ತೆಗೆದರೆ ಅದು
(i) 2 ಅಂಕಿಯ ಒಂದು ಸಂಖ್ಯೆ (ii) ಒಂದು ಪೂರ್ಣ ವರ್ಗ ಸಂಖ್ಯೆ
(iii) 5 ರಿಂದ ಭಾಗವಾಗುವ ಒಂದು ಸಂಖ್ಯೆಯನ್ನು ಹೊಂದಿರುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

19. ಒಂದು ಮಗುವಿನಲ್ಲಿ ಒಂದು ದಾಳವಿದೆ. ಅದರ ಮುಖಗಳು ಈ ಕೆಳಗಿನಂತೆ ಅಕ್ಷರಗಳನ್ನು ತೋರಿಸುತ್ತಿವೆ.

ದಾಳವನ್ನು ಒಂದು ಸಲ ಎಸೆದಿದೆ (i) A (ii) D ಯನ್ನು ಪಡೆಯುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:
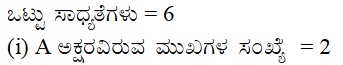
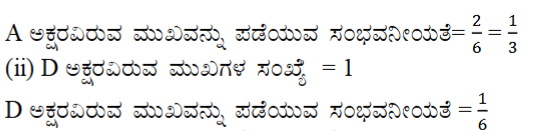
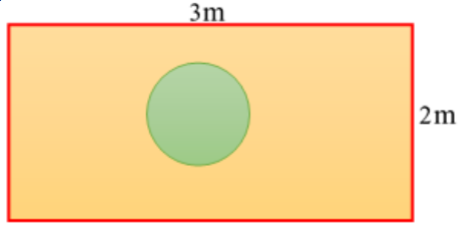
20. ಚಿತ್ರ 14.6 ರಲ್ಲಿ ತೋರಿಸಿದಂತೆ ನೀವು ಯಾದೃಚ್ಚಿಕವಾಗಿ ಒಂದು ದಾಳವನ್ನು ಆಯತಾಕಾರದ ಪ್ರದೇಶದಲ್ಲಿ ಬೀಳಿಸಿದ್ದೀರಿ ಎಂದು ಊಹಿಸಿಕೊಳ್ಳಿ. ಇದು 1 m ವ್ಯಾಸದ ವೃತ್ತಾಕಾರದೊಳಗೆ ನಿಲ್ಲುವ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:
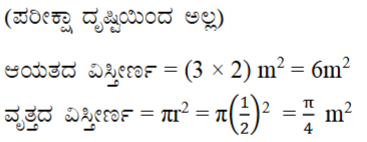
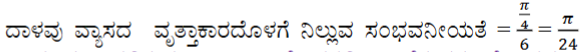
21. ಒಂದು ಗುಂಪಿನಲ್ಲಿರುವ 144 ಬಾಲ್ ಪೆನ್ ಗಳಲ್ಲಿ 20 ಪೆನ್ನುಗಳು ದೋಷಪೂರಿತವಾಗಿವೆ ಮತ್ತು ಉಳಿದವು ಉತ್ತಮವಾಗಿವೆ. ನೂರಿಯು ಪೆನ್ನು ಉತ್ತಮವಾಗಿದ್ದರೆ ಖರೀದಿಸುತ್ತಾನೆ. ಆದರೆ ದೋಷಪೂರಿತವಾಗಿದ್ದರೆ ಖರೀದಿಸುವುದಿಲ್ಲ ಅಂಗಡಿಯವನು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಒಂದು ಪೆನ್ನನ್ನು ತೆಗೆದುಕೊಂಡು ಆಕೆಗೆ ನೀಡುತ್ತಾನೆ.̈
(i) ಅವಳು ಇದನ್ನು ಖರೀದಿಸುವ
(ii) ಅವಳು ಇದನ್ನು ಖರೀದಿಸದ ಸಂಭವನೀಯತೆ ಎಷ್ಟು?
ಉತ್ತರ:

22.. ಉದಾಹರಣೆ 13 ನ್ನು (i) ನೋಡಿ ಕೋಷ್ಟಕವನ್ನು ಪೂರ್ಣಗೊಳಿಸಿ


ಉತ್ತರ:



23. ಒಂದು ಆಟದಲ್ಲಿ ಒಂದು ರೂಪಾಯಿಯ ಒಂದು ನಾಣ್ಯವನ್ನು 3 ಸಲ ಚಿಮ್ಮಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಪ್ರತಿ ಸಲದ ಫಲಿತವನ್ನು ದಾಖಲಿಸಲಾಗುತ್ತದೆ. ಹನೀಫನು, ಪ್ರತಿ ಸಲವೂ ಒಂದೇ ಫಲಿತಾಂಶ ಅಂದರೆ, 3 ಶಿರಗಳು ಅಥವಾ 3 ಪುಚ್ಚಗಳು ಬಂದರೆ, ಆಟದಲ್ಲಿ ಗೆಲ್ಲುತ್ತಾನೆ. ಇಲ್ಲದಿದ್ದರೆ ಸೋಲುತ್ತಾನೆ ಹನೀಫನು ಆಟದಲ್ಲಿ ಸೋಲುವ ಸಂಭವನೀಯತೆಯನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಿ.
ಉತ್ತರ:

24. ಒಂದು ದಾಳವನ್ನು 2 ಸಲ ಎಸೆಯಲಾಗಿದೆ.
(i) ಎರಡೂ ಸಲ 5 ಮೇಲೆ ಬರದಿರುವ
(ii) ಕನಿಷ್ಟ ಒಂದು ಸಲ 5 ಮೇಲೆ ಬರುವ ಸಂಭವನೀಯತೆಯು ಎಷ್ಟು?
[ಸುಳುಹು: ಒಂದು ದಾಳವನ್ನು ಎರಡು ಸಲ ಎಸೆಯುವುದು ಮತ್ತು ಎರಡು ದಾಳಗಳನ್ನು ಏಕಕಾಲದಲ್ಲಿ ಎಸೆಯುವುದು, ಈ ಎರಡೂ ಪ್ರಯೋಗಗಳನ್ನು ಒಂದೇ ಎಂದು ಪರಿಗಣಿಸುವುದು]
ಉತ್ತರ:

25. ಕೆಳಗಿನವುಗಳಲ್ಲಿ ವಾದಗಳು ಸರಿಯಾಗಿವೆ ಮತ್ತು ಯಾವುವು ತಪ್ಪಾಗಿವೆ ನಿಮ್ಮ ಉತ್ತರಕ್ಕೆ ಕಾರಣಗಳನ್ನು ನೀಡಿರಿ.
(i) ಎರಡು ನಾಣ್ಯಗಳನ್ನು ಏಕಕಾಲದಲ್ಲಿ ಚಿಮ್ಮಿಸಿದಾಗ, ಮೂರು ಸಾಧ್ಯ ಫಲಿತಗಳ ಇರುತ್ತವೆ – ಎರಡು ಶಿರಗಳು, ಎರಡು ಪುಚ್ಚಗಳು ಅಥವಾ ಪ್ರತಿಯೊಂದರಲ್ಲಿ ಒಂದರಂತೆ ಆದ್ದರಿಂದ ಈ ಪ್ರತಿಯೊಂದು ಫಲಿತಗಳ ಸಂಭವನೀಯತೆಯು 1/3
(ii) ಒಂದು ದಾಳವನ್ನು ಎಸೆದಾಗ, ಎರಡು ಸಾಧ್ಯ ಫಲಿತಗಳು ಇರುತ್ತವೆ – ಒಂದು ಬೆಸ ಸಂಖ್ಯೆ ಅಥವಾ ಒಂದು ಸಮಸಂಖ್ಯೆ ಆದ್ದರಿಂದ ಒಂದು ಬೆಸಸಂಖ್ಯೆ ಪಡೆಯುವ ಸಂಭವನೀಯತೆಯು 1/2
ಉತ್ತರ:

ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. ಸಾಮಾನ್ಯವಾಗಿ ಒಂದು ಪ್ರಯೋಗದ ಎಲ್ಲಾ ಪ್ರಾಥಮಿಕ ಘಟನೆಗಳ ಸಂಭವನೀಯತೆಗಳ ಮೊತ್ತವು 1 ಆಗಿರುತ್ತದೆ ಎಂಬುದು ಸತ್ಯವಾಗಿದೆ.
2. ಎಲ್ಲ ಪ್ರಯೋಗಗಳು, ‘ಸಮಾನ ಸಾಧ್ಯತೆಗಳ ಫಲಿತಗಳನ್ನು” ಹೊಂದಿರುತ್ತವೆ ಎಂದು ಊಹಿಸುತ್ತೇವೆ.
3. ಒಂದು ಘಟನೆಯ ಪ್ರಾಯೋಗಿಕ ಅಥವಾ ಅನುಭವ ವೇದ್ಯ ಸಂಭವನೀಯತೆಯು ವಾಸ್ತವವಾಗಿ ಏನು ಸಂಭವಿಸಿದೆಯೋ, ಅದನ್ನು ಅವಲಂಬಿಸಿದೆ ಹಾಗೆಯೇ ಒಂದು ಘಟನೆಯ ಸೈದ್ದಾಂತಿಕ ಸಂಭವನೀಯತೆಯು, ಕೆಲವು ಕಲ್ಪನೆಗಳ ಆಧಾರದಲ್ಲಿ ಏನು ಸಂಭವಿಸಬಹುದು ಎಂಬುದನ್ನು ಊಹಿಸಲು ಪ್ರಯತ್ನಿಸುತ್ತದೆ. ಒಂದು ಪ್ರಯೋಗದ ಯತ್ನಗಳ ಸಂಖ್ಯೆ ಹೆಚ್ಚುತ್ತಾ ಹೋದಂತೆ ಪ್ರಾಯೋಗಿಕ ಮತ್ತು ಸೈದ್ಧಾಂತಿಕ ಸಂಭವನೀಯತೆಗಳು ಸರಿ ಸುಮಾರಾಗಿ ಒಂದೇ ಎಂದು ನಾವು ನಿರೀಕ್ಷಿಸಬಹುದು.
4. ಖಚಿತವಾಗಿ (ಅಥವಾ ನಿಶ್ಚಿತವಾಗಿ) ಸಂಭವಿಸುವ ಒಂದು ಘಟನೆಯ ಸಂಭವನೀಯತೆಯು 1 ಆಗಿರುತ್ತದೆ. ಇಂತಹ ಘಟನೆಯನ್ನು ಖಚಿತ ಘಟನೆ ಅಥವಾ ನಿಶ್ಚಿತ ಘಟನೆ ಎನ್ನುತ್ತೇವೆ.

ಇತರೆ ವಿಷಯಗಳು :
ಗಣಿತ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಗಳು ಮತ್ತು ಘನಫಲಗಳು ನೋಟ್ಸ್
ಗಣಿತದಲ್ಲಿನ ಸಾಧನೆಗಳು ಗಣಿತ ನೋಟ್ಸ್
