10th Standard Samantara Shredigalu Maths Notes Question Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, 10ನೇ ತರಗತಿ ಗಣಿತ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳು ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು, 10th Standard Samantara Shredigalu Question and Answer, 10ನೇ ತರಗತಿ ಗಣಿತ ಪ್ರಶ್ನೋತ್ತರಗಳು pdf, 10th maths notes pdf kannada medium Part – 1, samantara shredigalu 10th class, samantara shredigalu lesson in kannada, ಸಮಾಂತರ ಶ್ರೇಢಿಗಳು 4 marks question, samantara shredigalu in kannada, 10th Question Answer kseeb solutions for class 10 maths chapter 1 in kannada, 10th standard maths 1st lesson notes in kannada medium, 10th class maths 1.1 kannada medium karnataka, sslc maths important questions with answers 1st chapter, sslc maths 1st chapter notes in kannada medium.
ಭಾಗ -1
ಘಟಕ 01 -ಸಮಾಂತರ ಶ್ರೇಢಿಗಳು
10ನೇ ತರಗತಿ ಗಣಿತ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳು ನೋಟ್ಸ್
ಅಭ್ಯಾಸ 1.1
1. ಈ ಕೆಳಗಿನ ಯಾವ ಸಂದರ್ಭಗಳಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಸಂಖ್ಯಾಪಟ್ಟಿಯು ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನುಂಟು ಮಾಡುತ್ತದೆ ಮತ್ತು ಏಕೆ?
(i) ಒಂದು ಟ್ಯಾಕ್ಸಿಯ ಬಾಡಿಗೆ ಮೊದಲ ಕಿಲೋಮೀಟರ್ಗೆ ₹15 ಆಗಿದ್ದು ನಂತರದ ಪ್ರತಿ ಕಿಲೋಮೀಟರ್ಗೆ ₹ 8 ರಂತೆ ಇರುತ್ತದೆ.
ಉತ್ತರ:
ಪ್ರಶ್ನೆಯಲ್ಲಿ ಗಮನಿಸಿದ ಹಾಗೆ,
ಟ್ಯಾಕ್ಸಿ ಬಾಡಿಗೆ ಮೊದಲ ಕಿಲೋಮೀಟರ್ಗೆ = 15
ಮೊದಲ ಎರಡು ಕಿಲೋಮೀಟರ್ ಗೆ = 15 + 8 = 23
ಮೊದಲ ಮೂರು ಕಿಲೋಮೀಟರ್ ಗೆ = 23 + 8 = 31
ಮೊದಲ ನಾಲ್ಕು ಕಿಲೋಮೀಟರ್ಗೆಗೆ = 31 + 8 = 39
15, 23, 31, 39…… ಸಂಖ್ಯಾ ಪಟ್ಟಿಯು ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನುಂಟು ಮಾಡುತ್ತದೆ ಏಕೆಂದರೆ ಪ್ರತಿಯೊಂದು ಪದದ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸವು 8 ಆಗಿದೆ.
(ii) ಒಂದು ನಿರ್ವಾತಗೊಳಿಸುವ ವಾಯು ರೇಚಕ ಯಂತ್ರವು ಪ್ರತಿಸಲ ಸಿಲಿಂಡರಿನಲ್ಲಿರುವ ಅನಿಲದ 1/4 ರಷ್ಟು ಅನಿಲವನ್ನು ಹೊರತೆಗೆದರೆ ಉಳಿಯುವ ಅನಿಲದ ಪ್ರಮಾಣಗಳು.
ಉತ್ತರ:
ಸಿಲಿಂಡರ್ನಲ್ಲಿರುವ ಆರಂಭಿಕ ವಾಯು V ಆಗಿರಲಿ. ಪ್ರತಿಸಲವೂ, ವಾಯು ರೇಚಕ ಯಂತ್ರವು ಸಿಲಿಂಡರ್ನಲ್ಲಿರುವ ಅನಿಲದ 1/4 ರಷ್ಟು ಅನಿಲವನ್ನು ಹೊರತೆಗೆಯುತ್ತದೆ.
ಪ್ರತಿಸಲ 1/4 ರಷ್ಟು ಅನಿಲವನ್ನು ಹೊರತೆಗೆದಾಗ ಉಳಿಯುವ ಅನಿಲದ ಪ್ರಮಾಣವು 1 – 1/4 = 3/4 ರಷ್ಟು ಆಗಿರುತ್ತದೆ.
ಆದ್ದರಿಂದ ಅದೇ ರೀತಿ ಉಳಿಯುವ ಅನಿಲದ ಪ್ರಮಾಣವು
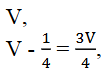
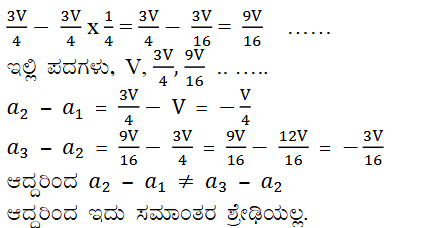
ಗಮನಿಸಿ ನೋಡಿದಾಗ ಪ್ರತಿ ಪದದ ವ್ಯತ್ಯಾಸವು ಒಂದೇ ಆಗಿಲ್ಲವಾದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿಲ್ಲ.
(iii) ಬಾವಿಯನ್ನು ತೋಡುವಾಗ ಮೊದಲ ಮೀಟರ್ಗೆ ₹150 ನಂತರದ ಪ್ರತಿ ಮೀಟರ್ಗೆ ₹ 50 ರಂತೆ ಹೆಚ್ಚಾಗುತ್ತಾ ಹೋಗುತ್ತದೆ.
ಉತ್ತರ:
1 ಮೀಟರ್ ತೋಡಲು ತಗಲುವ ವೆಚ್ಚ = 150
2 ಮೀಟರ್ ತೋಡಲು ತಗಲುವ ವೆಚ್ಚ = 150 + 50 = 200
3 ಮೀಟರ್ ತೋಡಲು ತಗಲುವ ವೆಚ್ಚ = 200 + 50 = 250
4 ಮೀಟರ್ ತೋಡಲು ತಗಲುವ ವೆಚ್ಚ = 250 + 50 = 300
ಗಮನಿಸಿ ನೋಡಿದಾಗ 150, 200, 250, 300…… ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನುಂಟುಮಾಡುತ್ತದೆ.
ಪ್ರತಿಯೊಂದು ಪದವು ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ 50ನ್ನು ಹೊಂದಿದೆ.
(iv) ಆರಂಭಿಕ ಠೇವಣಿ ₹ 10000 ಕ್ಕೆ 8% ಚಕ್ರಬಡ್ಡಿಯಂತೆ ಪ್ರತಿವರ್ಷ ಆಗುವ ಮೊತ್ತ
ಉತ್ತರ:
ಅಸಲು ರೂ P ಯನ್ನು r% ದರದಂತೆ n ವರ್ಷಗಳಿಗೆ ಆಗುವ ಚಕ್ರಬಡ್ಡಿ
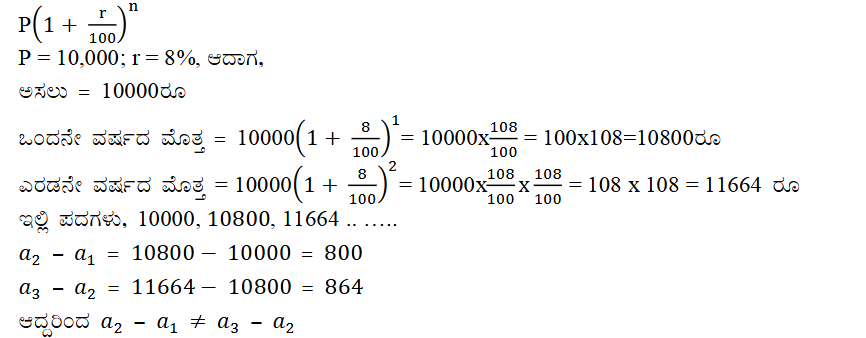
.’. ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲ
2. ಮೊದಲನೆ ಪದ 3, ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d . ಕೆಳಗಿನಂತಿರುವ ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ನಾಲ್ಕು ಪದಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) a = 10 d = 10
ಉತ್ತರ:
ಉ. a = 10 d = 10
a1 = 10
a2 = a1 + d = 10 + 10 = 20
a3 = a2 + d = 20 + 10 = 30
a4 = a3 + d = 30 + 10 = 40
a5 = a4 + d = 40 + 10 = 50
.’. ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ನಾಲ್ಕು ಪದಗಳು 10, 20, 30, 40, 50.
(ii) a = – 2 d = 0
ಉತ್ತರ:
(ii) a = – 2 d = 0
a1 = – 2
a2 = a1 + d = – 2 + 0 = – 2
a3 = a2 + d = – 2 + 0 = – 2
a4 = a3 + d = – 2 + 0 = – 2
a5 = a4 + d = – 2 + 0 = – 2
.’. ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ನಾಲ್ಕು ಪದಗಳು -2, -2, -2, -2
(iii) a = 4 d = – 3
ಉತ್ತರ:
a = 4 d = – 3
a1 = 4
a2 = a1 = d= 4 + (- 3) = 4 – 3 = 1
a3 = a2 + d = 1 – 3 = – 2
a4 = a3 + d = – 2 – 3 = – 5
a5 = a4 + d = – 5 – 3 = – 8
.’. ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ನಾಲ್ಕು ಪದಗಳು 4, 1, -2, -5.
(iv) a = – 1 d = 1/2
ಉತ್ತರ:
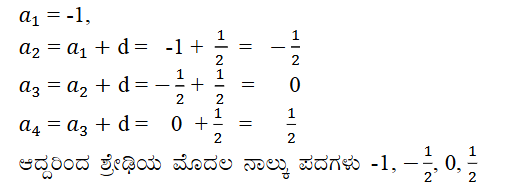
v) a = – 1.25 d = – 0.25
ಉತ್ತರ:
a2 = a + d
= -1.25+(-0.25)
= -1.25-0.25 =-1.5
a3 = a + 2d
= -1.25+2(-0.25)
= -1.25-0.5 =-1.75
a4 = a + 3d
= -1.25+3(-0.25)
= -1.25-0.75= -2
.’. ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ನಾಲ್ಕು ಪದಗಳು -1.25, -1.5, -1.75 -2.
3. ಕೆಳಗಿನ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳಿಗೆ ಮೊದಲನೇ ಪದ ಮತ್ತು ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸಗಳನ್ನು ಬರೆಯಿರಿ.
(i) 3, 1,-1,-3, …ʼ
ಉತ್ತರ:
a = 3 d = a2 – a1 = 1 – 3
d = – 2
.’. a = 3 d = – 2
(ii) -5,-1, 3, 7, …
ಉತ್ತರ:
a = – 5
d = a2 – a1 = – 1 – (- 5)
d = – 1 + 5 = 4
.’. a = 5, d=4
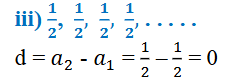
iv) 0.6, 1.7, 2.8, 3.9, …..
ಉತ್ತರ:
a=0.6
d= a2 – a1 = 1.7 – 0.6
d = 1.1
a=0.6, d = 1.1
4. ಇವುಗಳಲ್ಲಿ ಯಾವುವು ಸಮಾಂತರ ಶ್ರೇಢಿಗಳಾಗಿವೆ? ಸಮಾಂತರ ಶ್ರೇಢಿಗಳಾಗಿದ್ದಲ್ಲಿ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ ಕಂಡುಹಿಡಿದು ಅದರ ಮುಂದಿನ ಮೂರು ಪದಗಳನ್ನು ಬರೆಯಿರಿ.
(i) 2, 4, 8, 16, …
ಉತ್ತರ:
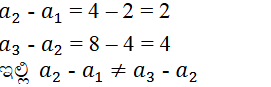
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲ
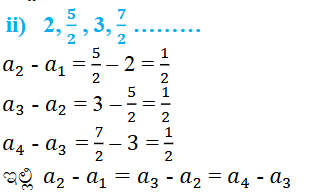
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ ಹೌದು
ಸಮಾಂತರ ಶ್ರೇಢಿ ಮುಂದಿನ ಮೂರು ಪದಗಳು
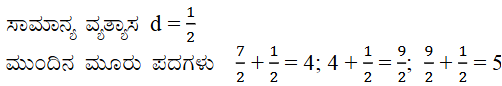
iii) -1.2, -3.2, -5.2, -7.2 …..
ಉತ್ತರ:
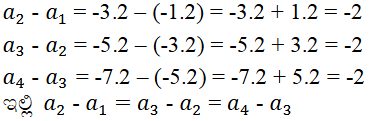
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ ಹೌದು
ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d = -2
ಮುಂದಿನ ಮೂರು ಪದಗಳು
a5 = a + 4d = -1.2 + 4(-2) = -1.2 – 8 = -9.2
a6 = a + 5d = -1.2 + 5(-2) = -1.2 – 10 = −11.2
a7 = a + 6d = -1.2 + 6(-2) = −1.2 – 12 = -13.2
v) -10, -6, -2, 2 ……
ಉತ್ತರ:
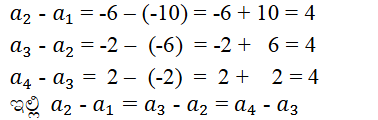
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ ಹೌದು
ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d = 4
a5 = a + 4d = -10 + 4(4) = -10 + 16 = 6
a6 = a + 5d = -10 + 5(4) = -10 + 20 = 10
a7 = a + 6d = -10 + 6(4) = -10 + 24 = 14
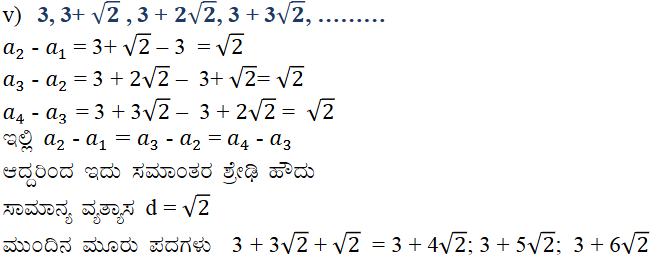
vi) 0.2, 0.22, 0.222, 0.2222 …………
ಉತ್ತರ:
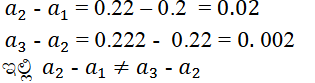
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲ
vii) 0, -4, -8, -12 ………
ಉತ್ತರ:
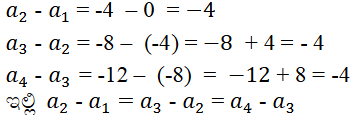
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ ಹೌದು
ಮುಂದಿನ ಮೂರು ಪದಗಳು
a5 = a + 4d = 0 + 4(-4) = -16
a6 = a + 5d = 0 + 5(-4) = -20
a7 = a + 6d = 0 + 6(-4) = -24
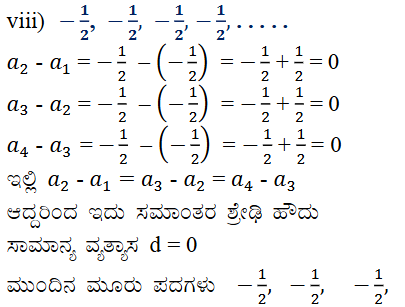
ix) 1, 3, 9, 27 ……….
ಉತ್ತರ:
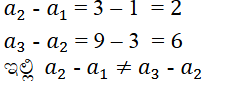
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ ಅಲ್ಲ
x) a, 2a, 3a, 4a ……..
ಉತ್ತರ:
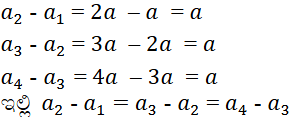
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ ಹೌದು
ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d = a
a5 = a + 4d = a+ 4(a) = 5a
a6 = a + 5d = a+ 5(a) = 6a
a7 = a + 6d = a+ 6(a) = 7a
xi) a, a2, a3, a4…..
ಉತ್ತರ:
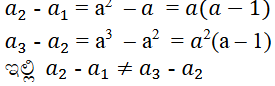
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲ
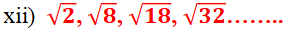
ಉತ್ತರ:

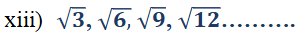
ಉತ್ತರ:
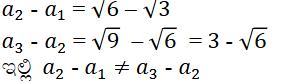
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲ
xiv) 12, 32, 52, 72
ಉತ್ತರ:
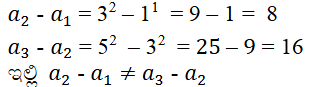
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲ
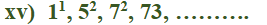
ಉತ್ತರ:
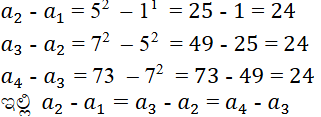
ಆದ್ದರಿಂದ ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿ
ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d= 24
a5 = a + 4d = 1+ 4(24) = 97
a6 = a + 5d = 1+ 5(24) = 121
a7 = a + 6d = 1+ 6(24) = 145
ಅಭ್ಯಾಸ 1.2
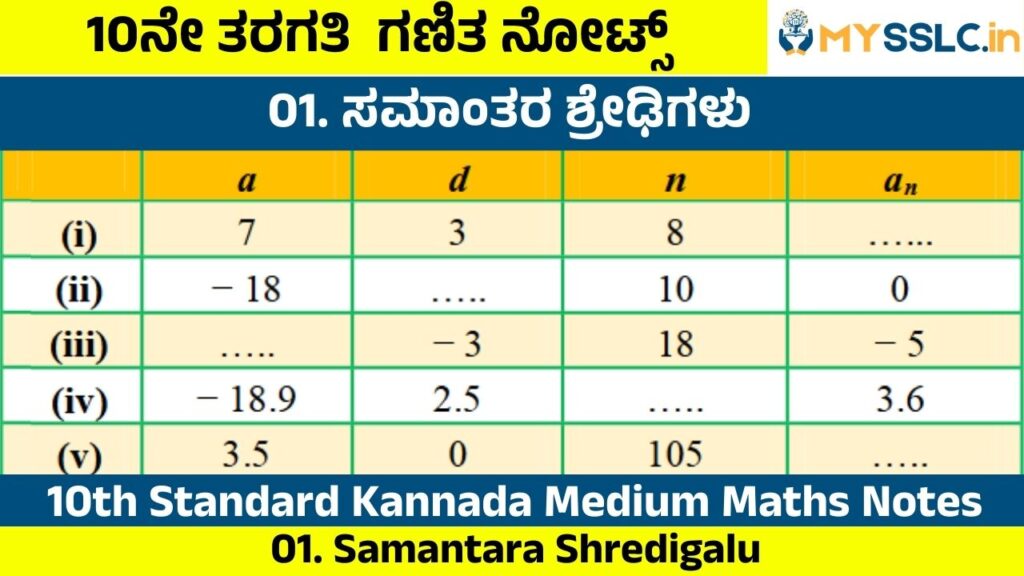
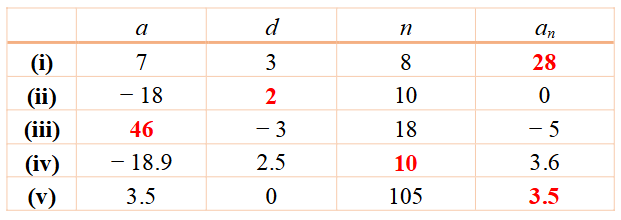
1. ಕೆಳಗಿನ ಕೋಷ್ಟಕದಲ್ಲಿ ಬಿಟ್ಟಿರುವ ಜಾಗಗಳನ್ನು ತುಂಬಿಸಿ, ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ಪದ 4, ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d, nನೇ ಪದ an ಆಗಿದೆ.
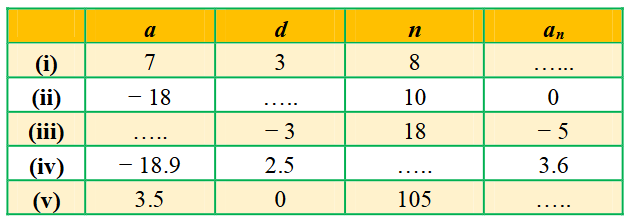
ಉತ್ತರ:
i) a = 7, d = 3, n = 8, an = ?
an = a + (n – 1)d
= 7 + (8 – 1)3
= 7 + (7)3
an = 28
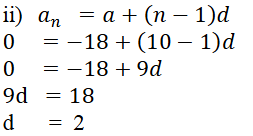
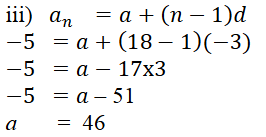
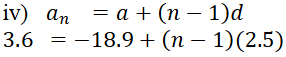
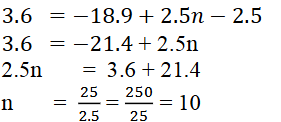
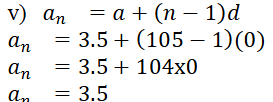
2. ಕೆಳಗಿನವುಗಳಲ್ಲಿ ಸರಿಯಾದ ಆಯ್ಕೆಯನ್ನು ಆರಿಸಿ ಸಮರ್ಥಿಸಿ
i) 10, 7, 4,…. ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯ 30ನೇ ಪದ
(A) 97 (B) 77 (C) -77 (D) -87
ಉತ್ತರ:
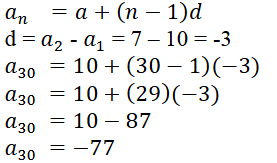
ಉತ್ತರ: (C) -77

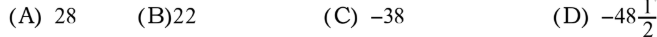
ಉತ್ತರ:
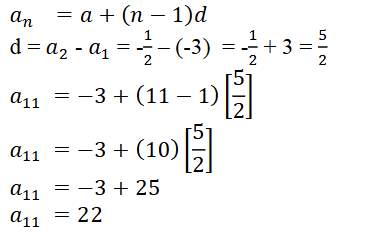
ಉತ್ತರ: (b) 22
3. ಕೆಳಗಿನ ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಬಾಕ್ಸ್ ಗಳಲ್ಲಿ ಖಾಲಿ ಬಿಟ್ಟಿರುವ ಪದಗಳನ್ನು ತುಂಬಿರಿ.
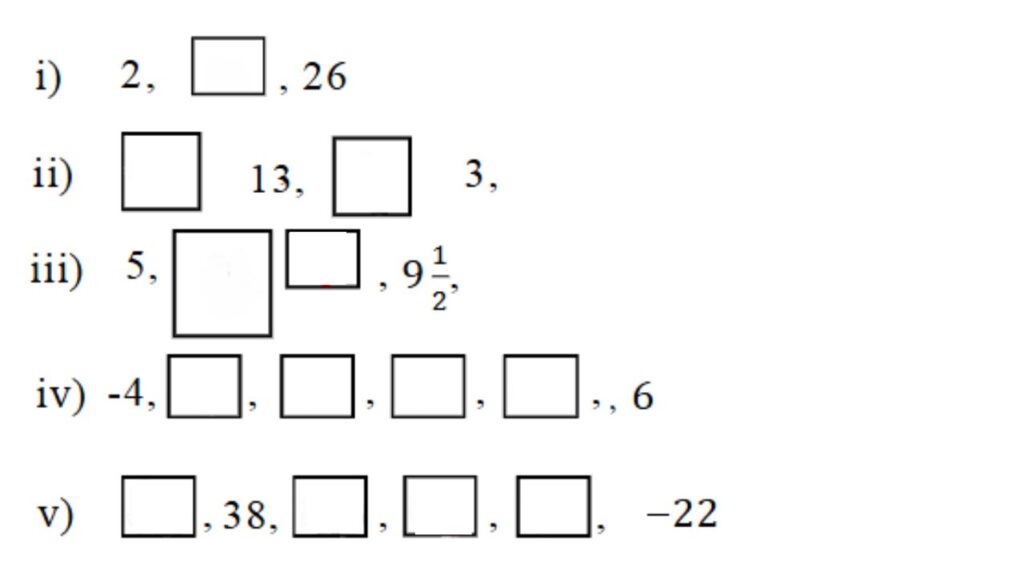
ಉತ್ತರ:
(i)
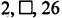
a = 2, a + d =?, a + 2d = 26
a + 26 = 26
2 + 2d = 26
2d = 24
∴ d=12 . .
∴ a + d = 2 + 12 = 14
ಖಾಲಿ ಬಿಟ್ಟ ಪದ 14
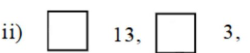
a =?, a + d = 13, a + 2d=?
a + 3d = 3
a + d + 2d = 3
13 + 2d = 3
2d = 3 – 13
2d = -10
∴ d = -5
a + d = 13
a + (-5) = 13
a – 5 = 13
∴ a – 13 + 5 = 18
∴ a = 18
a + 2d =?
= 18 + 2(-5)
= 18 – 10
a + 2d = 8
ಖಾಲಿ ಬಿಟ್ಟ ಪದ 18 ಮತ್ತು 8

a = 5, a + d =?, a + 2d =?
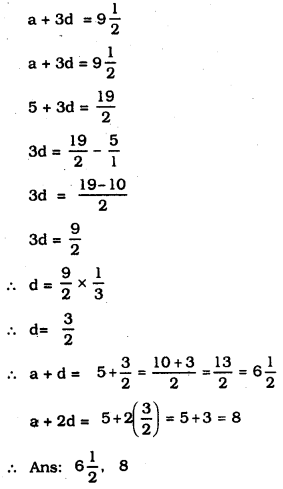

a = -4, a +d=? a + 2d =?
a+3d = ? a + 4d =? a + 5d = 6
a + 5d = 6
-4 + 5d = 6
5d = 6 + 4
5d = 10
d=10/5
∴ d=2.
a + d = -4 + 2 = -2
a + 2d = -4 + 2 (2) = -4 + 4 = 0
a + 3d = -4 + 3 (2) = -4 + 6 = 2
a + 4d = -4 + 4 (2) = -4 + 8 = 4
ಖಾಲಿ ಬಿಟ್ಟ ಪದ -2, 0, 2 ಮತ್ತು 4

a =? a + d = 38, a + 2d =?
a + 3d =?, a + 4d =?a + 5d = 22
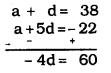
4d = -60
d= − (−60/4)=−15
a + d = 38
a – 15=38
a = 38 + 15 = 53
a + 2d = 53 + 2(-15) = 53 – 30 = 23
a + 3d = 53 + 3(-15) = 53 – 45 = 8
a + 4d =53 + 4(-15) = 53 – 60 = 7
ಖಾಲಿ ಬಿಟ್ಟ ಪದ 53, 23, 8 ಮತ್ತು -7.
4). 3, 8, 13, 18 ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಎಷ್ಟನೇ ಪದ 78?
ಉತ್ತರ:
a = 3, d = a2 – a1 = 8 – 3 = 5, an = 78, n =?
an = a + (n – 1) d
78 = 3+(n—1)(5)
78 = 3 + 5n – 5
78 = 5n – 2
5n = 78 + 2
n=80/5
∴ n = 16
ಸಮಾಂತರ ಶ್ರೇಢಿಯ 16ನೇ ಪದವು 78 ಆಗಿರುತ್ತದೆ.
5. ಈ ಕೆಳಗಿನ ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿರುವ ಪದಗಳ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) 7, 13, 19, ………. 205
ಉತ್ತರ:
a = 7, d = a2 – a1 = 13 – 7 = 6, an = 205, n =?
an = a + (n – 1) d
205 = 7 + (n – 1) 6
205 = 7 + 6n – 6
205 – 1 = 6n
204 = 6n
n=204/6
∴ n = 34
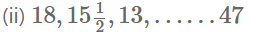
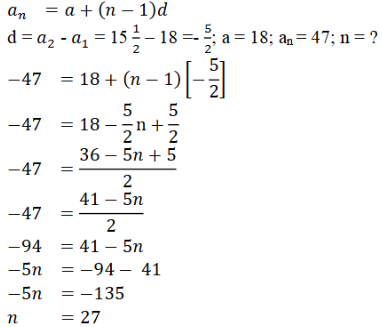
6). -150 ಇದು 11, 8, 5, 2 … ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಪದವಾಗಿದೆಯೇ ಪರೀಕ್ಷಿಸಿ.
ಉತ್ತರ:
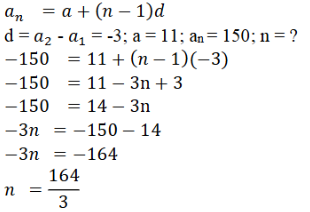
n ಒಂದು ಪೂರ್ಣಾಂಕ ಅಲ್ಲ, ಆದ್ದರಿಂದ -150 ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಪದವಲ್ಲ.
7). ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ 11ನೇ ಪದ 38, 16ನೇ ಪದ 73 ಆದರೆ 31ನೇ ಪದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
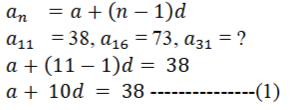
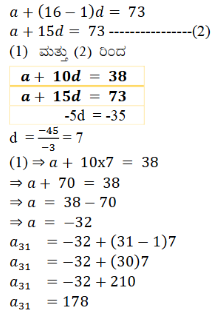
8). 50 ಪದಗಳನ್ನು ಹೊಂದಿರುವ ಸಮಾಂತರ ಶ್ರೇಢಿಯ 3ನೇ ಪದ 12 ಮತ್ತು ಕೊನೆಯ ಪದ 106 ಆದರೆ 29ನೇ ಪದ ಕಂಡುಹಿಡಿಯಿರಿ
ಉತ್ತರ:

9). ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ 3ನೇ ಮತ್ತು 9ನೇ ಪದಗಳು ಕ್ರಮವಾಗಿ 4 ಮತ್ತು -8 ಆದರೆ ಅದರ ಎಷ್ಟನೇ ಪದ ಸೊನ್ನೆಯಾಗಿದೆ?
ಉತ್ತರ:
a3 = 4, a9 = -8, an = 0, n =?
a3 = a + 2d = 4 ………….. (1)
a9 = a + 8d = -8 …………. (2)
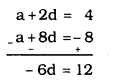
6d = 12
d=−12/6
∴ d = -2
a + 2d = 4
a – 2(2) = 4
a – 4 =4
∴ a = 4 + 4
∴ a = 8
an = a + (n – 1) d
= 8 + (n – 1) (-2)
= 8 – 2n + 2
= 10 – 2n = 0 ∵ an = 0
n=10/2
∴ n = 5
10). ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ 17ನೇ ಪದವು ಅದರ 10ನೇ ಪದಕ್ಕಿಂತ 7 ಹೆಚ್ಚಾಗಿದ್ದರೆ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
a17 = a10 + 7, d =?
a + 16d = a + 9d + 7
a +1 6d – a – 9d = 7
7d = 7
d=7/7
d = 1
∴ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸವು 1
11). 3, 15, 27, 39 … ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಯಾವ ಪದವು ಅದರ 54ನೇ ಪದಕ್ಕಿಂತ 132 ಹೆಚ್ಚಾಗಿದೆ?
ಉತ್ತರ:
3, 15, 27, 39, ………… an =?, n =?
an = a54 + 132
a = 3, d = 15 – 3 = 12
an = a54 + 132
an = a + 53d + 132
= 3 + 53(12) + 132
= 3 + 636 + 132
∴ an = 771
ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಎಷ್ಟನೇ ಪದವು 771ನೇ ಅಗುತ್ತದೆ ಎಂಬುವುದನ್ನು ಕಂಡು ಹಿಡಿಯಬೇಕು.
an = a + (n – 1) d = 771
= 3 + (n – 1)12 = 771
3 + 12n — 12 = 771
12n – 9 = 771
12n = 771 + 9
12n = 780
n=780/12
∴ n = 65.
12).ಎರಡು ಸಮಾಂತರ ಶ್ರೇಢಿಗಳ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ ಒಂದೇ ಆಗಿದೆ. ಅವುಗಳ 100ನೇ ಪದಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ 100 ಆದರೆ 1000ನೇ ಪದಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸವೇನು?
ಉತ್ತರ:

∴ ಸಮಾಂತರ ಶ್ರೇಢಿಯ 1000ನೇ ಪದಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ 100
13). ಮೂರು ಅಂಕಿಗಳ ಎಷ್ಟು ಸಂಖ್ಯೆಗಳು 7 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ?
ಉತ್ತರ:
105, 112, 119,……. 994.
a = 105, d = 112 – 105 = 7, an = 994, n =?
a + (n – 1)d = an
105 + (n – 1) 7 = 994
105 + 7n – 7 = 994
7n + 98 = 994
7n = 994 – 98
7n = 896
n=896/7
∴ n = 128
7 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುವ ಮೂರು ಅಂಕಿಯ ಸಂಖ್ಯೆಗಳು 128
14). 10 ಮತ್ತು 250ರ ನಡುವಿನ 4ರ ಗುಣಕಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು?
ಉತ್ತರ:
12, 16, 20, …….. 248
a = 12, d = 16 – 12 = 4
n =?
a = a + (n – 1) d = 248
12 + 4n – 4 = 248
4n + 8 = 248
4n = 248 – 8
4n = 240
n=240/4
∴ n = 60
10 ಮತ್ತು 250ರ ನಡುವಿನ 4ರ ಗುಣಕಗಳ ಸಂಖ್ಯೆ 60
15). n ನ ಯಾವ ಬೆಲೆಗೆ 63, 65, 67 …. ಮತ್ತು 3, 10, 17 … ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳ n ನೇ ಪದಗಳು ಸಮಾವಾಗಿರುತ್ತವೆ?
ಉತ್ತರ:
63, 65, 67,……….
a = 63. d = 65 – 63 =2. an =?
an = a + (n – 1)d
= 63 + (n – 1) 2
= 63 + 2n – 2
an= 2n + 61 …………….. (i)
3, 10, 17, ………….
a = 3, d = 10 – 3 = 7, an =?
an = a + (n – 1)d
= 3 + (n – 1) 7
= 3 + 7n – 7
an = 7n — 4 ………….(ii)
ಸಮೀಕರಣ (i) ಮತ್ತು (ii) ನ್ನು ಸಮೀಕರಿಸಿದಾಗ
2n + 61 = 7n – 4
2n – 7n = -4 – 61
5n = 65
5n =65
n=65/5
n = 13
∴ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳ 13ನೇ ಪದವು ಸಮನಾಗಿರುತ್ತವೆ.
16). ಮೂರನೇ ಪದ 16, 7ನೇ ಪದವು 5ನೇ ಪದಕ್ಕಿಂತ 12 ಹೆಚ್ಚಾಗಿರುವ ಸಮಾಂತರ ಶ್ರೇಢಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
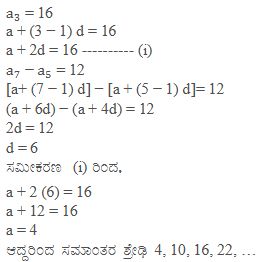
17). ಸಮಾಂತರ ಶ್ರೇಢಿ 3, 8, 13 … 253 ಇದರ ಕೊನೆಯಿಂದ ಆರಂಭಿಸಿ 20ನೇ ಪದ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

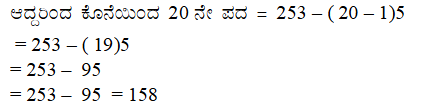
18). ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ 4ನೇ ಮತ್ತು 8ನೇ ಪದಗಳ ಮೊತ್ತ 24 ಮತ್ತು 6ನೇ ಮತ್ತು 10ನೇ ಪದಗಳ ಮೊತ್ತ 44 ಆದರೆ ಆ ಶ್ರೇಢಿಯ ಮೊದಲ ಮೂರು ಪದಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
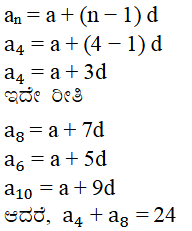
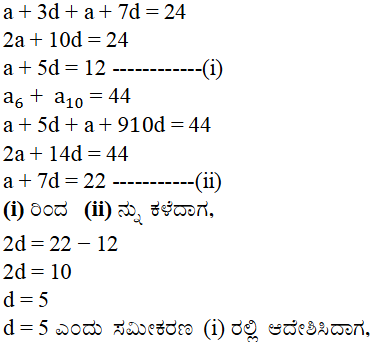

19). ವಾರ್ಷಿಕ ಸಂಬಳ ₹ 5000 ಮತ್ತು ಪ್ರತಿವರ್ಷಕ್ಕೆ ಹೆಚ್ಚುವರಿ ಭತ್ಯೆ ₹ 200 ಇರುವ ಕೆಲಸಕ್ಕೆ ಸುಬ್ಬರಾವ್ 1995 ರಲ್ಲಿ ಸೇರಿದರು. ಯಾವ ಯಾವ ವರ್ಷದಲ್ಲಿ ಅವರ ಸಂಬಳ 7000 ಆಗುತ್ತದೆ?
ಉತ್ತರ:
a = 5000, d = 5200 – 5000 = 200,
an = 7000, n=?
a + (n – 1)d = an
5000 + (n – 1) 200 = 7000
5000 + 200n – 200 = 7000
200n + 4800 = 7000
200n = 7000 – 4800
200n = 2200
n=2200/200
n = 11
∴ 11ನೇ ವರ್ಷದಲ್ಲಿ ಅವರ ಸಂಬಳವು 7000 ಆಗುತ್ತದೆ.
20). ರಾಮ್ಕಲಿಯು ವರ್ಷದ ಮೊದಲನೇ ವಾರದಲ್ಲಿ ₹5 ನ್ನು ಉಳಿಸಿದಳು ಮತ್ತು ಪ್ರತಿವಾರ ಅವಳ ಉಳಿತಾಯವನ್ನು ₹1.75ಕ್ಕೆ ಹೆಚ್ಚಿಸಿದಳು. nನೇ ವಾರದಲ್ಲಿ ಅವಳ ಉಳಿತಾಯ ₹20.76 ಆದರೆ n ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
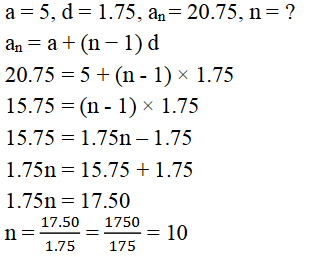
ಅಭ್ಯಾಸ 1.3
1. ಕೆಳಗಿನ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳ ಮೊತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
i) 2, 7, 12, ……… ರ 10 ಪದಗಳವರೆಗೆ
ಉತ್ತರ:
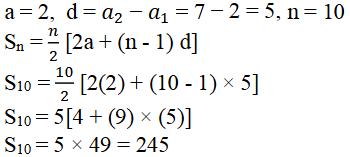
ii) -37, -33, -29,………. ರ 12 ಪದಗಳವರೆಗೆ
ಉತ್ತರ:
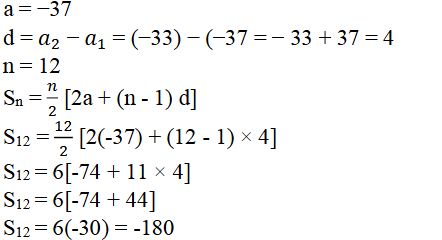
iii) 0.6, 1.7, 2.8 …. ರ 100 ಪದಗಳವರೆಗೆ
ಉತ್ತರ:
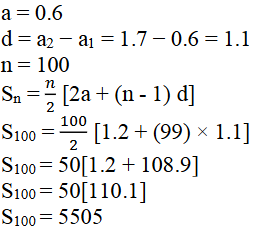

ಉತ್ತರ:
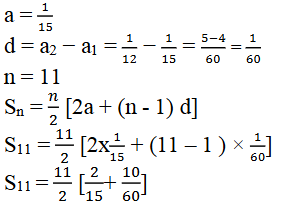
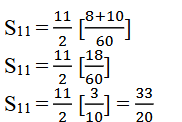
2. ಇವುಗಳ ಮೊತ್ತ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
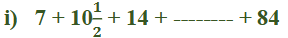
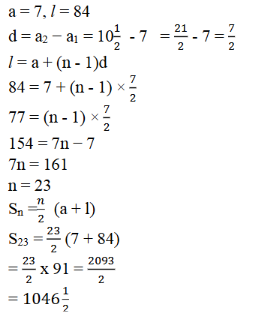
ii) 34 + 32 + 30 + ………. + 10
ಉತ್ತರ:
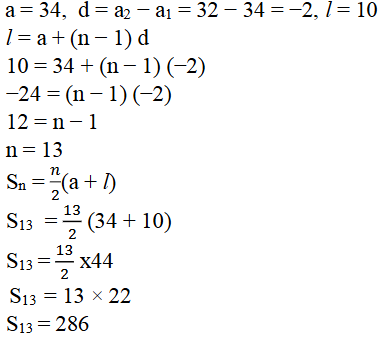
iii) -5 + (-8) + (-11) +……… + (-230)
ಉತ್ತರ:
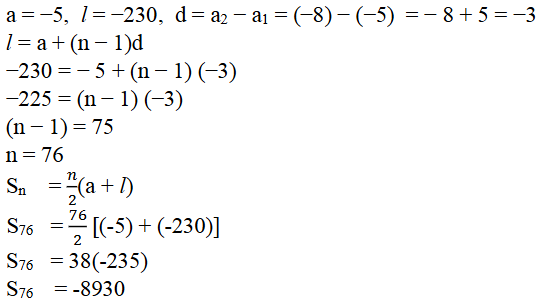
3. ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿ
i) a = 5, d = 3, an = 50, ಆದರೆ n ಮತ್ತು Sn ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
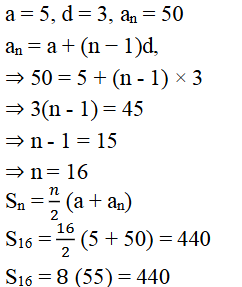
ii) a = 7, a13 = 35 ಆದರೆ d ಮತ್ತು S13 ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
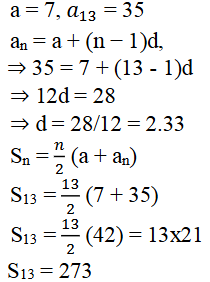
iii) a12= 37, d = 3 ಆದರೆ a ಮತ್ತು S12 ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
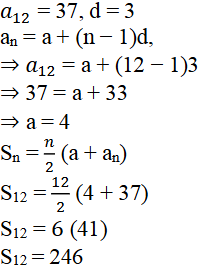
iv) a3 = 15, S10 = 125, ಆದರೆ d ಮತ್ತು a10 ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
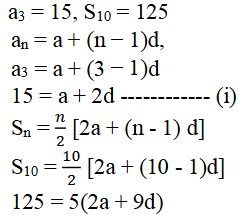

v) d = 5, S9 = 72, ಆದರೆ a ಮತ್ತು a9 ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
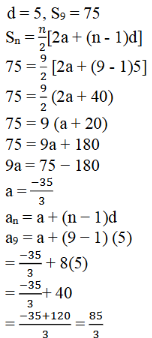
vi) a = 2, d = 8, Sn = 90, ಆದರೆ a ಮತ್ತು an ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
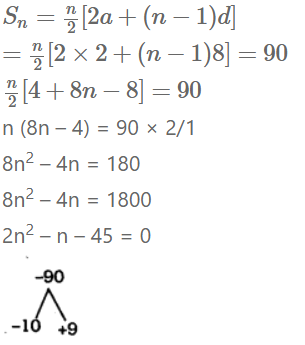
2n2– 10n + 9n – 45 = 0
2n(n – 5) + 9(n – 5) = 0
(n – 5)(2n + 9) = 0
n – 5 = 0 ಆದರೆ n = 5
∴ an = a + (n – 1) d
a5= 2 + (5 – 1) 8
= 2 + 4 × 8
= 2 + 32
∴ a5 = 34
vii) a = 8, an = 62, Sn = 210, ಆದರೆ n ಮತ್ತು d ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
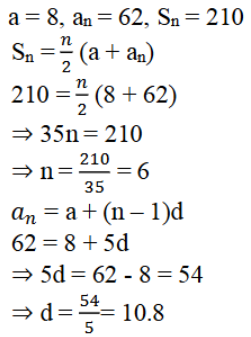
viii) an = 4, d = 2, Sn = -14 ಆದರೆ n ಮತ್ತು a ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
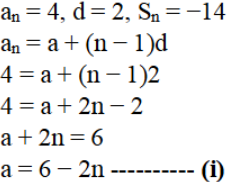
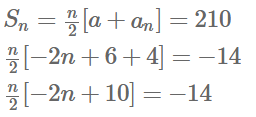
-2n2 + 10n = -28
-2n2 + 10n + 28 = 0
2n2 – 10n – 28 = 0 – 14
2n2 – 5n – 14 = 0
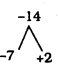
n2 – 7n + 2n – 14 = 0
n(n – 7) + 2 (n – 7) = 0
(n – 7) (n + 2) = 0
n – 7 = 0 ಆದರೆ n = 7
a = -2n + 6
= -2 × 7 + 6
= -14 + 6
∴ a = -8
∴ n = 7, a = -8
ix) a = 3, n = 8, S = 192, ಆದರೆ d ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
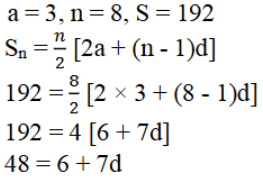
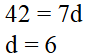
x) L = 28, S = 144 ಮತ್ತು ಪದಗಳ ಸಂಖ್ಯೆ 9 ಇದ್ದರೆ a ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
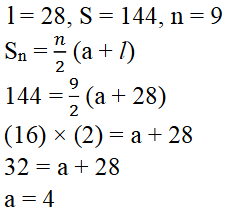
4. ಮೊತ್ತ 636 ಸಿಗಬೇಕಾದರೆ 9, 17, 25… ಈ ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಎಷ್ಟು ಪದಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಬೇಕಾಗುತ್ತದೆ?
ಉತ್ತರ:
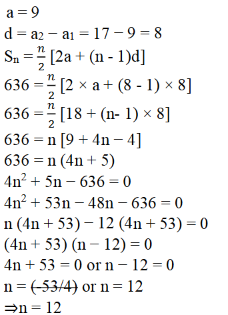
5. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿ ಮೊದಲ ಪದ 5, ಕೊನೆಯ ಯ ಪದ 45 ಮತ್ತು ಮೊತ್ತ 400 ಆದರೆ ಅದರ ಪದಗಳ ಸಂಖ್ಯೆ ಮತ್ತು ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ ಕಂಡುಹಿಡಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
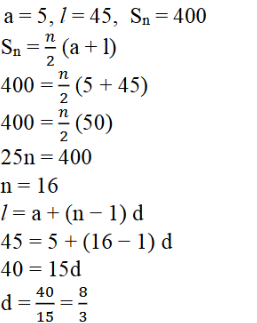
6. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ಮತ್ತು ಕೊನೆಯ ಪದಗಳು ಕ್ರಮವಾಗಿ 17 ಮತ್ತು 350 ಆಗಿವೆ. ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ 9 ಆದರೆ ಪದಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು ಮತ್ತು ಅವುಗಳ ಮೊತ್ತ ಎಷ್ಟು?
ಉತ್ತರ:
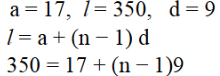
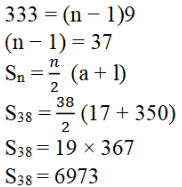
7. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಲ್ಲಿ d = 7 ಮತ್ತು ಮತ್ತು 22 ನೇ ಪದ 149 ಆದರೆ 22 ಪದಗಳವರೆಗಿನ ಮೊತ್ತವೇನು?
ಉತ್ತರ:
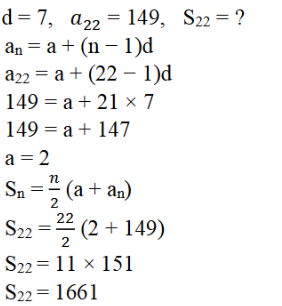
8. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಎರಡನೇ ಮತ್ತು ಮೂರನೇ ಪದಗಳು ಕ್ರಮವಾಗಿ 14 ಮತ್ತು 18 ಆದರೆ ಅದರ 51 ಪದಗಳವರೆಗಿನ ಮೊತ್ತವೇನು?
ಉತ್ತರ:
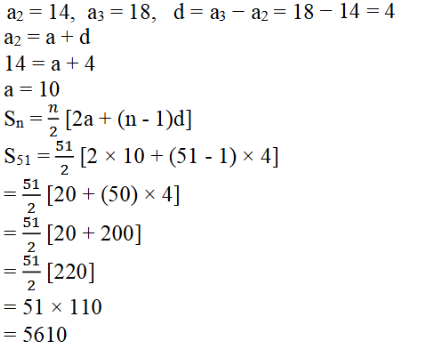
9. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ 7 ಪದಗಳವರೆಗಿನ ಮೊತ್ತ 49 ಮತ್ತು 17 ಪದಗಳವರೆಗಿನ ಮೊತ್ತ 289. ಆದರೆ ಮೊದಲ n ಪದಗಳವರೆಗಿನ ಮೊತ್ತವೇನು?
ಉತ್ತರ:
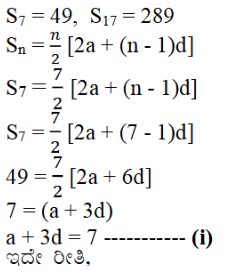

10. an ಈ ಕೆಳಗಿನಂತೆ ನಿರೂಪಿಸಲ್ಪಟ್ಟಾಗ a1, a2, a3, … an…. ಇದು ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ ಎಂದು ತೋರಿಸಿ
i) an= 3 + 4n ii) an = 9 – 5n
ಉತ್ತರ:
i) an= 3 + 4n
a1 = 3 + 4(1) = 7
a2 = 3 + 4(2) = 3 + 8 = 11
a3 = 3 + 4(3) = 3 + 12 = 15
a4 = 3 + 4(4) = 3 + 16 = 19
⇒ a2 − a1 = 11 − 7 = 4
a3 − a2 = 15 − 11 = 4
a4 − a3 = 19 − 15 = 4
i.e., ak + 1 − ak ಒಂದೇ ಬೆಲೆಯಾಗಿರುವುದರಿಂದ ಇಂದು ಸಮಾಂತರ ಶ್ರೇಢಿ.
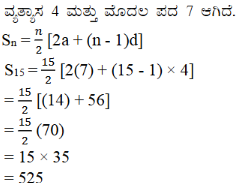
ii) an = 9 – 5n
ಉತ್ತರ:
a1 = 9 − 5 × 1 = 9 − 5 = 4
a2 = 9 − 5 × 2 = 9 − 10 = −1
a3 = 9 − 5 × 3 = 9 − 15 = −6
a4 = 9 − 5 × 4 = 9 − 20 = −11
⇒ a2 − a1 = − 1 − 4 = −5
a3 − a2 = − 6 − (−1) = −5
a4 − a3 = − 11 − (−6) = −5
i.e., ak + 1 − ak ಒಂದೇ ಬೆಲೆಯಾಗಿರುವುದರಿಂದ ಇಂದು ಸಮಾಂತರ ಶ್ರೇಢಿ.
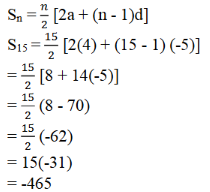
11. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ n ಪದಗಳವರೆಗಿನ ಮೊತ್ತ 4n – n² ಆದರೆ ಮೊದಲ ಪದ (S1) ಎಷ್ಟು? bಮೊದಲ ಎರಡು ಪದಗಳ ಮೊತ್ತವೇನು? ಎರಡನೇ ಪದ ಎಷ್ಟು? ಅದೇ ರೀತಿ 3ನೇ ಪದ, 10ನೇ ಪದ ಮತ್ತು nನೇ ಪದಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
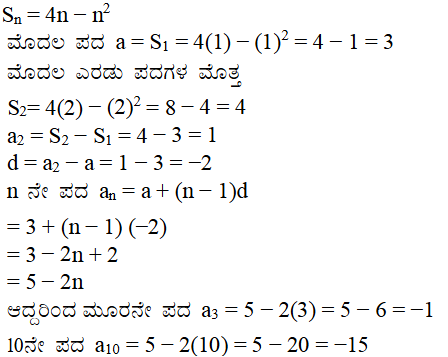
12. 6 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುವ ಮೊದಲ 40 ಧನಾತ್ಮಕ ಪೂರ್ಣಾಂಕಗಳ ಮೊತ್ತವೇನು?
ಉತ್ತರ:
6, 12, 18, 24 …
ಇದು ಸಮಾಂತರ ಶ್ರೇಢಿಯಾಗಿದ್ದು ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ 6 ಮತ್ತು ಮೊದಲ ಪದ 6 ಆಗಿದೆ
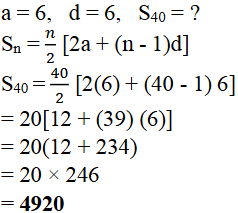
13. ಮೊದಲ 15, 8ರ ಅಪವರ್ತ್ಯಗಳ ಮೊತ್ತವೇನು?
ಉತ್ತರ:
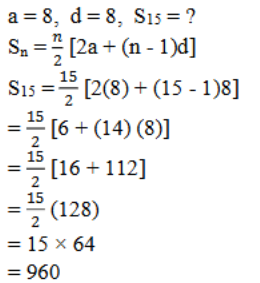
14. 0 ಮತ್ತು 50 ರ ನಡುವಿನ ಬೆಸ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತವೇನು?
ಉತ್ತರ:
ಹೇಳಿಕೆಯಂತೆ 1, 3, 5, 7, 9 … 49
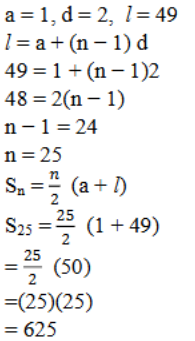
15. ಕಟ್ಟಡವೊಂದರ ಕೆಲಸದ ಗುತ್ತಿಗೆಗೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಮಯದ ನಂತರ ತಡವಾಗಿ ಕೆಲಸ ಪೂರ್ಣಗೊಳಿಸಿದರೆ, ನಿರ್ದಿಷ್ಟ ರೂಪದ ದಂಡವನ್ನು ವಿಧಿಸಲಾಗಿತ್ತು. ಅದು ಹೀಗಿದೆ: ಮೊದಲನೇ ದಿನಕ್ಕೆ ₹ 200, ಎರಡನೇ ದಿನಕ್ಕೆ ₹ 250, 3ನೇ ದಿನಕ್ಕೆ ₹ 300 ಇತ್ಯಾದಿ. ಪ್ರತಿ ದಿನದ ದಂಡವು ಅದರ ಹಿಂದಿನ ದಿನದ ದಂಡಕ್ಕಿಂತ ₹ 50 ಜಾಸ್ತಿ ಹಾಗಾದರೆ ಒಬ್ಬ ಗುತ್ತಿಗೆದಾರನು ಒಂದು ಕೆಲಸವನ್ನು ಪೂರ್ತಿಗೊಳಿಸಲು 30 ದಿನಗಳ ಕಾಲ ಹೆಚ್ಚು ತೆಗೆದುಕೊಂಡರೆ ಅವನು ಕೊಡಬೇಕಾದ ದಂಡವನ್ನು ಲೆಕ್ಕಚಾರ ಮಾಡಿ?
ಉತ್ತರ:

16. ಒಂದು ಶಾಲೆಯ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಮಗ್ರ ವಾರ್ಷಿಕ ನಿರ್ವಹಣೆಗಾಗಿ ನಗದು ಬಹುಮಾನಕ್ಕಾಗಿ ₹700ರ ಮೊತ್ತವನ್ನು ನೀಡಲಾಗಿತ್ತು. ಪ್ರತಿ ಬಹುಮಾನವು ಅದರ ಮುಂಚಿನ ಬಹುಮಾನಕ್ಕಿಂತ ₹ 20 ಕಡಿಮೆಯಾದರೆ ಪ್ರತಿ ಬಹುಮಾನಗಳ ಮೌಲ್ಯ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
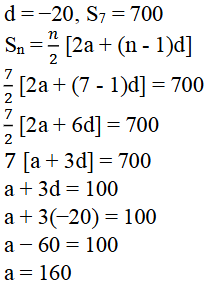
17. ವಾಯುಮಾಲಿನ್ಯವನ್ನು ಕಡಿಮೆ ಮಾಡಲು ಒಂದು ಶಾಲೆಯ ವಿದ್ಯಾರ್ಥಿಗಳು ಶಾಲೆಯ ಒಳ ಆವರಣ ಮತ್ತು ಹೊರ ಆವರಣ ಗಿಡಗಳನ್ನು ನೆಡುವ ಯೋಚನೆ ಮಾಡಿದರು. ಪ್ರತಿ ತರಗತಿಯ ಪ್ರತಿ ವಿಭಾಗದಲ್ಲಿ ನೆಡುವ ಗಿಡಗಳ ಸಂಖ್ಯೆಯು ಅವರು ಅಧ್ಯಯನ ಮಾಡುತ್ತಿರುವ ತರಗತಿಯ ಸಂಖ್ಯೆಗೆ ಸಮವಾಗಿರಬೇಕೆಂದು ತಿರ್ಮಾನಿಸಲಾಗಿದೆ. ಉದಾ: 1ನೇ ತರಗತಿಯ ಒಂದು ವಿಭಾಗವು 1 ಗಿಡವನ್ನು, ಎರಡನೇ ತರಗತಿಯ ವಿಭಾಗವು 2 ಗಿಡಗಳನ್ನು ಹೀಗೆ 12ನೇ ತರಗತಿಗಳವರೆಗೆ ಮುಂದುವರಿದಿದೆ. ಪ್ರತಿ ತರಗತಿಯಲ್ಲಿ ಮೂರು ವಿಭಾಗಗಳಿದ್ದರೆ ವಿದ್ಯಾರ್ಥಿಗಳು ನೆಡಬೇಕಾದ ಗಿಡಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು?
ಉತ್ತರ:
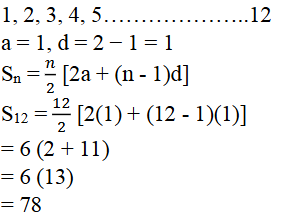
ಆದ್ದರಿಂದ ಪ್ರತಿ ತರಗತಿಯಲ್ಲೂ 3 ವಿಭಾಗಗಳಿದ್ದರೆ ವಿದ್ಯಾರ್ಥಿಗಳು ನೆಡಬೇಕಾದ ಒಟ್ಟು ಗಿಡಗಳ ಸಂಖ್ಯೆ = 3 x 78 = 234
18. ಒಂದು ಸುರುಳಿಯನ್ನು ಕ್ರಮಾಗತ ಅರೆ ವೃತ್ತಗಳಿಂದ ಮಾಡಲಾಗಿದೆ ಅವುಗಳ ಕೇಂದ್ರಗಳು ಪರ್ಯಾಯವಾಗಿ A ಮತ್ತು B ನಲ್ಲಿದ್ದು A ಕೇಂದ್ರದಿಂದ ಆರಂಭವಾಗಿ ತ್ರಿಜ್ಯಗಳು 0.5cm, 1cm, 1.5cm, 2cm….. ಹೀಗೆ ಚಿತ್ರ 1.4 ರಲ್ಲಿ ತೋರಿಸಿದಂತೆ ಇದೆ. ಈ ರೀತಿ ಹದಿಮೂರು ಕ್ರಮಾಗತ ಅರೆ ವೃತ್ತಗಳಿಂದ ವೃತ್ತಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟ ಸುರುಳಿಯ ಒಟ್ಟು ಉದ್ದ ಏನು?

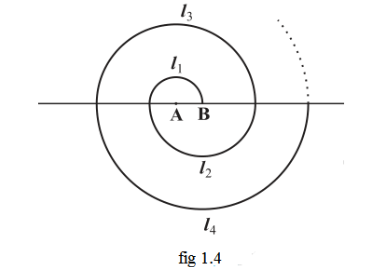
ಉತ್ತರ:
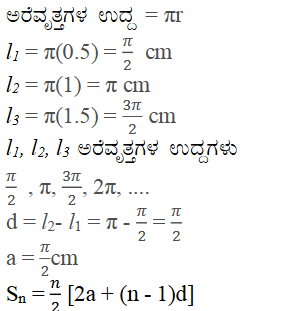
ಆದ್ದರಿಂದ ಹದಿಮೂರು ಕ್ರಮಾನುಗತ ಅರೆ ವೃತ್ತಗಳಿಂದ ಮಾಡಲ್ಪಟ್ಟ ಸುರುಳಿಯ ಒಟ್ಟು ಉದ್ದ
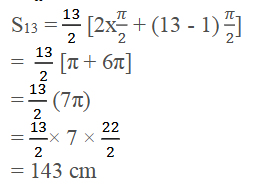
19. 200 ಮರದ ದಿಮ್ಮಿ (ಕೊರಡು)ಗಳನ್ನು ಕೆಳಗಡೆ ಸೂಚಿಸಿರುವಂತೆ ಒಂದರ ಮೇಲೊಂದನ್ನು ಜೋಡಿಸಲಾಗಿದೆ. ಕೆಳಭಾಗದ ಸಾಲಿನಲ್ಲಿ 19 ದಿ ಮ್ಮಿಗಳು ಆ ನಂತರದ ಸಾಲಿನಲ್ಲಿ 18 ದಿಮ್ಮಿಗಳು ಹೀಗೆ ಮುಂದುವರಿದಿದೆ. (ಚಿತ್ರ 1.5ನ್ನು ನೋಡಿ) 200 ದಿಮ್ಮಿಗಳನ್ನು ಎಷ್ಟು ಸಾಲುಗಳಲ್ಲಿ ಇಡಲಾಗಿದೆ ಮತ್ತು ಅತ್ಯಂತ ಮೇಲ್ಬಾಗದ ಸಾಲಿನಲ್ಲಿರುವ ದಿಮ್ಮಿಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು?
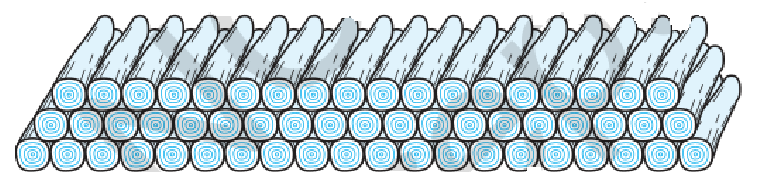
ಉತ್ತರ:
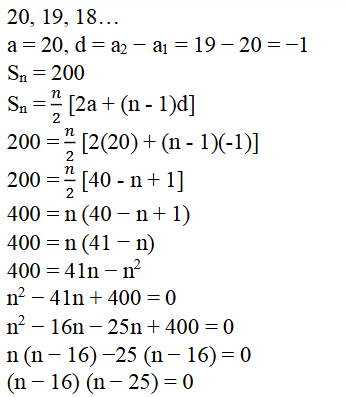
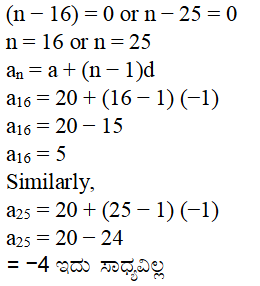
200 ದಿಮ್ಮಿಗಳನ್ನು 16 ಸಾಲಿಗಳಲ್ಲಿ ಇಡಲಾಗಿದೆ ಹಾಗೂ ಅತ್ಯಂತ ಮೇಲ್ಭಾಗದ ಸಾಲಿನಲ್ಲಿರುವ ದಿಮ್ಮಿಗಳ ಸಂಖ್ಯೆ = 5
20. ಒಂದು ಅಲೂಗಡ್ಡೆ ಓಟದಲ್ಲಿ ಒಂದು ಬುಟ್ಟಿಯನ್ನು ಪ್ರಾರಂಭದಲ್ಲಿ ಮೊದಲನೇ ಆಲೂಗಡ್ಡೆಯಿಂದ 5m ದೂರದಲ್ಲಿ ಇಡಲಾಗಿದೆ ಉಳಿದ ಆಲೂಗಡ್ಡೆಗಳನ್ನು ಒಂದೇ ರೇಖೆಯ ಮೇಲೆ ಪರಸ್ಪರ 3m ಅಂತರದಲ್ಲಿ ಇಡಲಾಗಿದೆ. ಆ ರೇಖೆಯ ಮೇಲೆ ಒಟ್ಟು 10 ಆಲೂಗಡ್ಡೆಗಳಿವೆ. (ಚಿತ್ರ 1.6 ನ್ನು ನೋಡಿ)

ಒಬ್ಬ ಸ್ಪರ್ಧಿಯು ಬಕೆಟ್ನಿಂದ ಆರಂಭಿಸಿ ಅದರ ಸಮೀಪದಲ್ಲಿರುವ ಆಲೂಗಡ್ಡೆಯನ್ನು ತೆಗೆದುಕೊಂಡು ಹಿಂದಕ್ಕೆ ಓಡಿ ಬಕೆಟ್ಗೆ ಹಾಕಬೇಕು. ನಂತರ ಅಲ್ಲಿಂದ ಪುನಃ ಓಡಿ 2ನೆ ಆಲೂಗಡ್ಡೆಯನ್ನು ತೆಗೆದುಕೊಂಡು ಹಿಂದಕ್ಕೆ ಓಡಿ ಬಕೆಟಿಗೆ ಹಾಕಬೇಕು. ಅವಳು ಇದೇ ರೀತಿ ಎಲ್ಲಾ ಆಲೂಗಡ್ಡೆಗಳು ಬಕೆಟ್ನಲ್ಲಿ ಬಂದು ಬೀಳುವವರೆಗೂ ಮುಂದುವರಿಸಬೇಕು. ಸ್ಪರ್ಧಿಯು ಓಡಿದ ಒಟ್ಟು ದೂರವೇನು?
[ಸುಳುಹು: ಮೊದಲನೇ ಮತ್ತು 2ನೇ ಆಲೂಗಡ್ಡೆಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲು ಸ್ಪರ್ಧಿಯು ಓಡಿದ ಒಟ್ಟು ದೂರ (m ಗಳಲ್ಲಿ ) 2 × 5 +2 × (5 + 3)]
ಉತ್ತರ:
5, 8, 11, 14…..
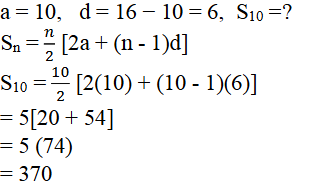
ಸ್ಪರ್ಧಿಯು ಓಡಿದ ಒಟ್ಟು ದೂರ = 370
ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
- ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ಪದ a1, ಎರಡನೇ ಪದ a2….. nನೇ ಪದ an, ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d ಆಗಿರಲಿ. ಆಗ ಸಮಾಂತರ ಶ್ರೇಢಿಯು a1, a2, a3 ……. an= ಆಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ a2– a1 = a3 – a2 =…………= an-1 = d
- ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಸಾಮಾನ್ಯ ಪದ an = a + (n – 1)d
- ಮೊದಲ ಪದವನ್ನು ಹೊರತುಪಡಿಸಿ ಪ್ರತಿಯೊಂದು ಪದವನ್ನು ಪಡೆಯಲು ಅದರ ಹಿಂದಿನ ಪದಕ್ಕೆ ಒಂದು ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯನ್ನು ಕೂಡಿಸುವುದರಿಂದ ಪಡೆಯುವ ಸಂಖ್ಯಾ ಪಟ್ಟಿಯೇ ಸಮಾಂತರ ಶ್ರೇಢಿ.
- ಸಮಾಂತದ ಶ್ರೇಢಿಯ ಸಾಮಾನ್ಯ ರೂಪ a, a + b, a + 2d, a + 3d………. a + (n – 1)d
- ನಿರ್ದಿಷ್ಟ ಪದಗಳ ಸಂಖ್ಯೆಯನ್ನು ಮಾತ್ರ ಹೊಂದಿರುವ ಸಮಾಂತರ ಶ್ರೇಢಿಗೆ ಪರಿಮಿತ ಸಮಾಂತರ ಶ್ರೇಢಿ ಎನ್ನುತ್ತಾರೆ.
- ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಮೊದಲ ಪದ a ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ d ಆದಾಗ ಅದರ n ನೇ ಪದವು an = a + (n – 1)d
- ಸ್ಥಿರ ಸಂಖ್ಯೆಯನ್ನು ಸಮಾಂತರ ಶ್ರೇಢಿಯ ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸ ಎನ್ನುತ್ತಾರೆ.
ಇತರೆ ವಿಷಯಗಳು :
10ನೇ ತರಗತಿ ಗಣಿತ ತ್ರಿಭುಜಗಳು ನೋಟ್ಸ್
ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು ನೋಟ್ಸ್
