10th Standard Melmai Vistirnagalu Mattu Ghanaphalagalu Maths Notes Question Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 10ನೇ ತರಗತಿ ಗಣಿತ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಗಳು ಮತ್ತು ಘನಫಲಗಳು ನೋಟ್ಸ್, 10th Class Melmai Vistirnagalu Mattu Ghanaphalagalu Notes Pdf 10th Class Maths Notes 10ನೇ ತರಗತಿ ಗಣಿತ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಗಳು ಮತ್ತು ಘನಫಲಗಳು ನೋಟ್ಸ್ Pdf melmai vistirnagalu mattu ghanaphalagalu 10th notes, ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಗಳು ಮತ್ತು ಘನಫಲಗಳು 10ನೇ ತರಗತಿ ಗಣಿತ ನೋಟ್ಸ್, 10th standard maths notes.
ಘಟಕ 15 – ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಗಳು ಮತ್ತು ಘನಫಲಗಳು
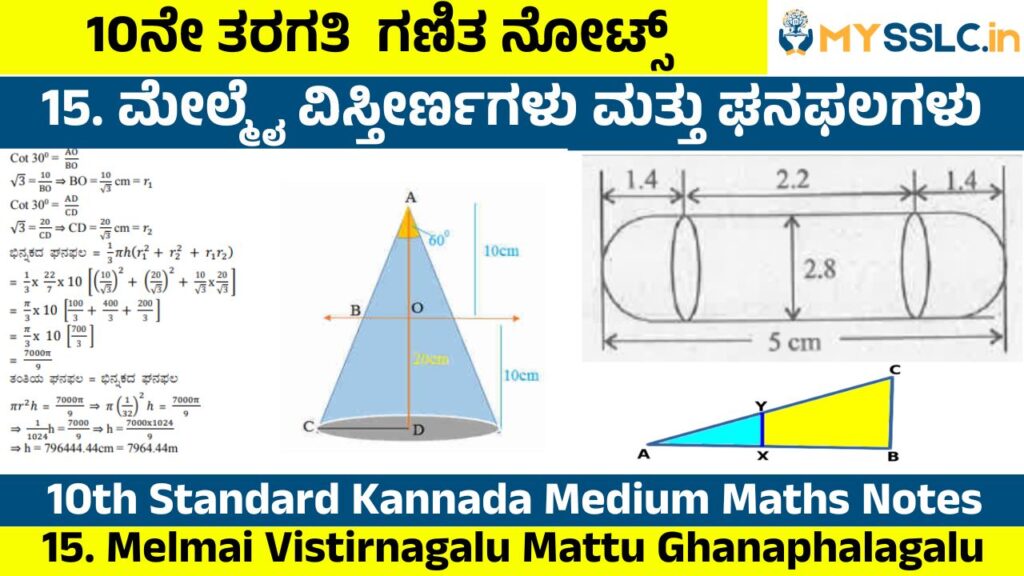
ಅಭ್ಯಾಸ 15.1
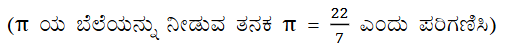
1. 64 cm² ಘನಫಲವನ್ನು ಹೊಂದಿರುವ 2 ವರ್ಗ ಘನಗಳ ಮುಖಗಳನ್ನು ಸೇರಿಸಿ ಒಂದು ಆಯತ ಘನಾಕೃತಿ ಮಾಡಿದೆ. ಈ ಆಯತ ಘನಾಕೃತಿಯ ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

2. ಒಂದು ಪಾತ್ರೆಯ ಆಕಾರವು ಟೊಳ್ಳಾದ ಸಿಲಿಂಡರಿನ ಒಂದು ಪಾದದ ಮೇಲೆ ಟೊಳ್ಳಾದ ಅರ್ಧಗೋಳಾಕೃತಿಯನ್ನು ಕೂಡಿಸಿ ಮಾಡಿದೆ. ಅರ್ಧಗೋಳದ ವ್ಯಾಸವು 14 cm ಮತ್ತು ಪಾತ್ರೆಯ ಒಟ್ಟು ಎತ್ತರವು 13 cm ಇದೆ. ಈ ಪಾತ್ರೆಯ ಒಳ ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

3. ಒಂದು ಅರ್ಧಗೋಳದ ಮೇಲೆ ಅದೇ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವ ಒಂದು ಶಂಕುವನ್ನು ಕೂಡಿಸಿ ಒಂದು ಆಟಿಕೆಯನ್ನು ಮಾಡಿದೆ. ಅವೇರಡರ ವೃತ್ತಾಕಾರದ ಪಾದದ ತ್ರಿಜ್ಯವು 3.5 cm ಆಗಿದೆ. ಆಟಿಕೆಯ ಒಟ್ಟು ಎತ್ತರವು 15.5 cm ಆದರೆ ಆಟಿಕೆಯ ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

4. ಪ್ರತಿ ಅಂಚು 7 cm ಹೊಂದಿರುವ ವರ್ಗ ಘನಾಕೃತಿಯ ಒಂದು ವಸ್ತುವಿನ ಮೇಲ್ಮುಖದ ಮೇಲೆ ಅರ್ಧಗೋಳವು ಇರಿಸಿದೆ. ಅರ್ಧಗೋಳದ ಗರಿಷ್ಠ ವ್ಯಾಸವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ? ಈ ಪೂರ್ಣ ಘನಾಕೃತಿಯ ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

5. ವರ್ಗ ಘನಾಕೃತಿಯ ಮರದ ವಸ್ತುವಿನ ಒಂದು ಮುಖದ ಒಳಭಾಗವು ತಗ್ಗಾಗುವಂತೆ ಅರ್ಧಗೋಳವನ್ನು ಕೊರೆಯಲಾಗಿದೆ. ವರ್ಗ ಘನದ ಅಂಚಿನ ಉದ್ದವು ಅರ್ಧಗೋಳದ ವ್ಯಾಸ l ಗೆ ಸಮನಾಗಿದ್ದರೆ, ನೂತನವಾಗಿ ಉಂಟಾದ ಘನದ ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

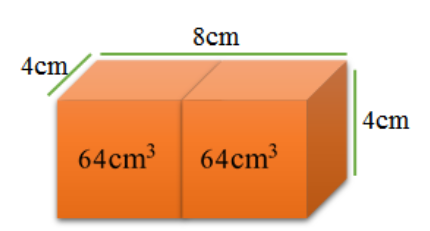
6. ಒಂದು ಔಷದದ ಕ್ಯಾಪ್ಸುಲ್ನ ಆಕಾರವು ಒಂದು ಸಿಲಿಂಡರಿನ ಪ್ರತಿ ಪಾದಗಳಲ್ಲಿ ಎರಡು ಅರ್ಧಗೋಳವನ್ನು ಅಂಟಿಸಿದೆ. (ಚಿತ್ರ 15.10 ನೋಡಿ). ಕ್ಯಾಪ್ಸುಲ್ನ ಸಂಪೂರ್ಣ ಉದ್ದವು 14 mm ಮತ್ತು ಅದರ ವ್ಯಾಸವು 5 mm ಇದೆ. ಅದರ ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
7. ಸಿಲಿಂಡರಿನ ವೃತ್ತಾಕಾರದ ಪಾದವನ್ನು ಶಂಕುವು ಸಂಪೂರ್ಣವಾಗಿ ಆವರಿಸುವಂತೆ ಒಂದು ಡೇರೆಯು ಇದೆ. ಸಿಲಿಂಡರಿನ ಎತ್ತರ ಮತ್ತು ವ್ಯಾಸವು 2.1 m ಮತ್ತು 4 m ಕ್ರಮವಾಗಿ ಇದೆ ಮತ್ತು ಶಂಕುವಿನ ಓರೆ ಎತ್ತರ 2.8 m ಆದರೆ, ಡೇರೆಯನ್ನು ನಿರ್ಮಿಸಲು ಬಳಸಿದ ತಾಡಪತ್ರಿ (canvas) ಯ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ಹಾಗೆಯೇ, ತಾಡಪತ್ರಿಯ ದರವು ರೂ 500 ಪ್ರತಿ ಚದರ ಮೀಟರ್ಗೆ ಆದರೆ, ತಾಡಪತ್ರಿಯನ್ನು ಕೊಳ್ಳಲು ಬೇಕಾಗುವ ಹಣವೆಷ್ಟು? (ಡೇರೆಯ ಪಾದವನ್ನು ತಾಡಪತ್ರಿಯಿಂದ ಹಾಸಿರುವುದಿಲ್ಲ ಎಂಬುದನ್ನು ಗಮನಿಸಿ).
ಉತ್ತರ:

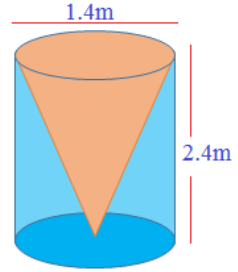
8. ಒಂದು ಘನ ಸಿಲಿಂಡರಿನ ಎತ್ತರ 2.4 m ಮತ್ತು ವ್ಯಾಸ 1.4 m ಇದೆ. ಇದರಿಂದ ಒಂದೇ ಎತ್ತರ ಮತ್ತು ಒಂದೇ ವ್ಯಾಸವನ್ನು ಹೊಂದಿರುವ ಶಂಕುವಿನಾಕಾರದ ಹಳ್ಳವನ್ನು ಕೊರೆದು ಟೊಳ್ಳಗಿಸಿದೆ. ನೂತನ ಘನದ ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಅತ್ಯಂತ ಸಮೀಪದ ಬೆಲೆಗೆ cm² ನಲ್ಲಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

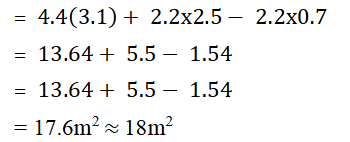
9. ಮರದಿಂದ ಮಾಡಿದ ಸಿಲಿಂಡರಿನ ಎರಡು ವೃತ್ತಕಾರದ ಅರ್ಧಗೋಳವನ್ನು ಚಿತ್ರ 15.11 ರಲ್ಲಿ ತೋರಿಸಿದಂತೆ ಕೊರೆದು ಒಂದು ವಸ್ತುವನ್ನು ತಯಾರಿಸಿದೆ. ಸಿಲಿಂಡರಿನ ಎತ್ತರ 10 cm ಮತ್ತು ಅದರ ಪಾದದ ತ್ರಿಜ್ಯ 3.5 cm ಆದರೆ, ವಸ್ತುವಿನ ಒಟ್ಟು ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

ಅಭ್ಯಾಸ 15.2
1. ಒಂದು ಘನದಲ್ಲಿ ಅರ್ಧಗೋಳದ ವೃತ್ತಾಕಾರದ ಪಾದದ ಮೇಲೆ ಸಂಪೂರ್ಣವಾಗಿ ಆವರಿಸುವಂತೆ ಶಂಕುವು ನಿಂತಿದೆ. ಅವುಗಳ ತ್ರಿಜ್ಯಗಳು 1 cm ಮತ್ತು ಶಂಕುವಿನ ಎತ್ತರವು ಅದರ ತ್ರಿಜ್ಯಕ್ಕೆ ಸಮನಾಗಿದೆ. ಈ ಘನದ ಘನಫಲವನ್ನು π ಯಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಿರಿ.
ಉತ್ತರ:

2. ರೇಚಲ್ ಒಬ್ಬ ಇಂಜಿನಿಯರಿಂಗ್ ವಿದ್ಯಾರ್ಥಿನಿ. ಅವರು ತೆಳುವಾದ ಅಲ್ಯುಮಿನಿಯಂ ಹಾಳೆಯಿಂದ ಸಿಲಿಂಡರಿನ ಎರಡು ವೃತ್ತ ಪಾದಗಳಲ್ಲಿ ಶಂಕುವನ್ನು ಜೋಡಿಸಿ ಒಂದು ಮಾದರಿಯನ್ನು ತಯಾರು ಮಾಡಬೇಕಾಗಿದೆ. ಈ ಮಾದರಿಯ ವ್ಯಾಸವು 3 cm ಮತ್ತು ಅದರ ಒಟ್ಟಾರೆ ಉದ್ದವು 12 cm ಇದೆ. ಶಂಕುವಿನ ಎತ್ತರವು 2 cm ಆದರೆ ರೆಚೇಲ್ ಮಾಡಿದ ಈ ಮಾದರಿಯೊಳಗಿನ ಗಾಳಿಯ ಗಾತ್ರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (ಮಾದರಿಯ ಹೊರ ಹಾಗೂ ಒಳ ಮೇಲೈ ಅಳತೆಗಳು ಸರಿಸುಮಾರಾಗಿ ಒಂದೇ ಆಗಿದೆ ಎಂದು ಭಾವಿಸಿಕೊಳ್ಳಿ).
ಉತ್ತರ:

3. ಒಂದು ಗುಲಾಬ್ ಜ್ಯಾಮ್ನ್ನಲ್ಲಿ ಅದರ ಘನಫಲದ ಶೇ 30 ರಷ್ಟು ಸಕ್ಕರೆಯ ಪಾಕವನ್ನು ಒಳಗೊಂಡಿದೆ. ಪ್ರತಿ ಗುಲಾಬ್ ಜ್ಯಾಮುನು ಸಿಲಿಂಡರ್ ಆಕಾರದಲ್ಲಿ ಇದ್ದು, ಅದರ ಎರಡು ಅಂತ್ಯ ಭಾಗದಲ್ಲಿ ಅರ್ಧಗೋಳಗಳಿವೆ. ಗುಲಾಬ್ ಜಾಮುನಿನ ಒಟ್ಟಾರೆ ಉದ್ದ 5cm ಮತ್ತು ವ್ಯಾಸವು 2.8cm ಆದರೆ, 45 ಗುಲಾಬ್ ಜ್ಯಾಮುನ್ನಲ್ಲಿ ಇರುವ ಸಕ್ಕರೆ ಪಾಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (ಚಿತ್ರ 15.15 ನೋಡಿ).
ಉತ್ತರ:
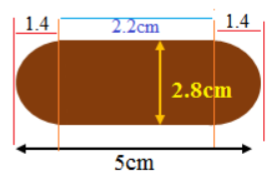

4. ಆಯತ ಘನಾಕೃತಿಯ ಆಕಾರದ ಮರದ ಲೇಖನಿಧಾರಕ (Pen stand) ದಲ್ಲಿ ಲೇಖನಿಗಳನ್ನು ಇಡಲು ಶಂಕುವಿನಾಕಾರದ ನಾಲ್ಕು ತಗ್ಗುಗಳನ್ನು ಕೊರೆದಿದೆ. ಆಯತ ಘನಾಕೃತಿಯ ಅಳತೆಯು 15cm x 10 cm x 3.5 cm ಆಗಿದೆ. ಪ್ರತಿ ಶಂಕುವಿನಾಕಾರದ ಹಳ್ಳದ ತ್ರಿಜ್ಯವು 0.5cm ಮತ್ತು ಆಳವು 1.4cm ಇದೆ. ಲೇಖನಿಧಾರಕದಲ್ಲಿನ ಮರದ ಗಾತ್ರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (ಚಿತ್ರ 15.16 ನೋಡಿ).
ಉತ್ತರ:

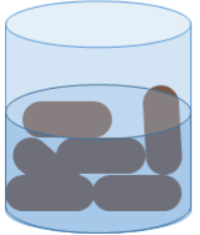
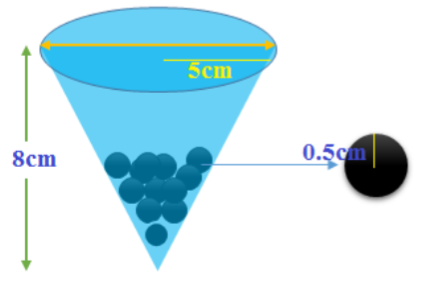
5. ಒಂದು ಪಾತ್ರೆಯು ತಲೆಕೆಳಗಾದ ಶಂಕುವಿನಾಕಾರದಲ್ಲಿದೆ. ಅದರ ಎತ್ತರ 8 cm ಮತ್ತು ತೆರೆದ ಮೇಲ್ಬಾಗದ ತ್ರಿಜ್ಯವು 5cm ಇದೆ. ಅದರ ಅಂಚಿನವರೆಗೆ ಪೂರ್ಣವಾಗಿ ನೀರನ್ನು ತುಂಬಿದೆ. ಅದರಲ್ಲಿ 0.5 cm ತ್ರಿಜ್ಯವಿರುವ ಸೀಸದ ಗೋಳಗಳನ್ನು ಪಾತ್ರೆಯಲ್ಲಿ ಹಾಕಿದಾಗ, ನಾಲ್ಕನೆಯ ಒಂದು ಭಾಗದಷ್ಟು ನೀರು ಹೊರ ಚಲ್ಲುತ್ತದೆ. ಪಾತ್ರೆಯಲ್ಲಿ ಹಾಕಿದ ಸೀಸದ ಗೋಳಗಳೆಷ್ಟು?
ಉತ್ತರ:
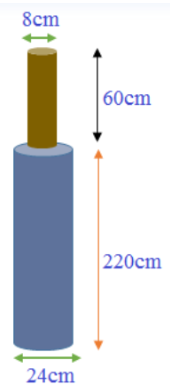
6. ಒಂದು ಕಬ್ಬಿಣದ ಕಂಬದ ಎತ್ತರವು 220cm ಮತ್ತು ಅದರ ಪಾದದ ವ್ಯಾಸವು 24cm ಆಗಿರುವ ಘನ ಸಿಲಿಂಡರಿನಾಕಾರದಲ್ಲಿ ಇದೆ. ಇದರ ಮೇಲೆ 60cm ಎತ್ತರ ಮತ್ತು ತ್ರಿಜ್ಯ 8cm ಇರುವ ಮತ್ತೊಂದು ಸಿಲಿಂಡರ್ ಜೋಡಿಸಲಾಗಿದೆ. 1 cm³ ಕಬ್ಬಿಣದ ಸರಿಸುಮಾರು ದ್ರವ್ಯರಾಶಿಯು 8g ಆದರೆ ಕಂಬದ ದ್ರವ್ಯರಾಶಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. (π = 3.14 ಎಂದು ತೆಗೆದುಕೊಳ್ಳಿ).
ಉತ್ತರ:

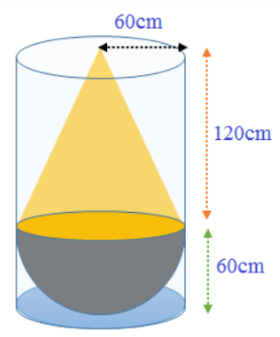
7. 60cm ತ್ರಿಜ್ಯವಿರುವ ಅರ್ಧಗೋಳದ ಪಾದದ ಮೇಲೆ 120 cm ಎತ್ತರ ಮತ್ತು 60cm ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವ ನೇರ ವೃತ್ತ ಪಾದ ಶಂಕುವನ್ನು ಜೋಡಿಸಲಾಗಿದೆ. ಸಂಪೂರ್ಣವಾಗಿ ನೀರಿನಿಂದ ತುಂಬಿದ ನೇರ ವೃತ್ತಪಾದ ಸಿಲಿಂಡರಿನಲ್ಲಿ ತಳವನ್ನು ಮುಟ್ಟುವಂತೆ ನೇರವಾಗಿ ಈ ಘನಾಕೃತಿಯನ್ನು ಮುಳುಗಿಸಲಾಗಿದೆ. ಸಿಲಿಂಡರಿನ ತ್ರಿಜ್ಯವು 60 cm ಮತ್ತು ಎತ್ತರವು 180cm ಆದರೆ ಸಿಲಿಂಡರಿನಲ್ಲಿ ಉಳಿದಿರುವ ನೀರಿನ ಪ್ರಮಾಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

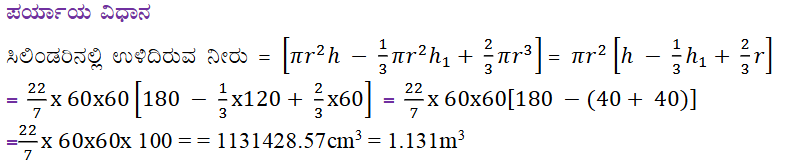
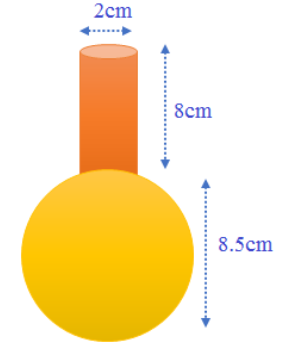
8. 8.5cm ವ್ಯಾಸವುಳ್ಳ ಒಂದು ಗೋಳಾಕಾರದ ಗಾಜಿನ ಪಾತ್ರೆಯು 8cm ಉದ್ದ ಮತ್ತು 2cm ವ್ಯಾಸವನ್ನು ಹೊಂದಿರುವ ಸಿಲಿಂಡರಿನ ಆಕಾರದ ಕೊರಳನ್ನು ಹೊಂದಿದೆ. ಒಂದು ಮಗುವು ಅದರಲ್ಲಿ ಹಿಡಿಯುವ ನೀರಿನ ಗಾತ್ರವನ್ನು ಅಳತೆ ಮಾಡುವುದರ ಮೂಲಕ ಅದರ ಘನಫಲವು 345 cm³ ಇದೆ ಎಂದು ಕಂಡುಕೊಳ್ಳುತ್ತಾಳೆ. ಮೇಲೆ ಕೊಟ್ಟಿರುವ ಅಳತೆಗಳು ಅದರ ಒಳಭಾಗದ ಅಳತೆಗಳು ಎಂದು ಭಾವಿಸಿ, ಅವಳ ಉತ್ತರವು ಸರಿಯಾಗಿದೆಯೇ ಎಂದು ಪರೀಕ್ಷಿಸಿ. (TT = 3.14 ಎಂದು ತೆಗೆದುಕೊಳ್ಳಿ).
ಉತ್ತರ:

ಅಭ್ಯಾಸ 15.3
1. 4.2 cm ತ್ರಿಜ್ಯವುಳ್ಳ ಲೋಹದ ಗೋಳವನ್ನು ಕರಗಿಸಿ ಅದನ್ನು 6 cm ತ್ರಿಜ್ಯವಿರುವ ಸಿಲಿಂಡರಿನ ಆಕಾರದಲ್ಲಿ ಮರುರೂಪ ನೀಡಲಾಗಿದೆ. ಸಿಲಿಂಡರಿನ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

2. 6 cm, 8 cm ಮತ್ತು 10 cm ತ್ರಿಜ್ಯಗಳನ್ನು ಹೊಂದಿರುವ ಲೋಹದ ಮೂರು ಗೋಳಗಳನ್ನು ಕರಗಿಸಿ ಒಂದು ಲೋಟದ ಗೋಳವನ್ನು ಮಾಡಿದೆ. ಹೀಗೆ ಉಂಟಾದ ನವೀನ ಗೋಳದ ತ್ರಿಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
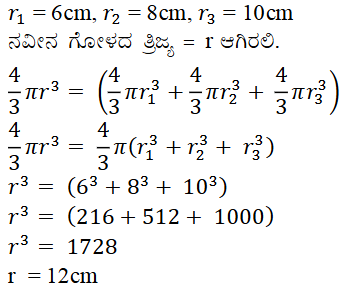
3. 20 m ಆಳ ಮತ್ತು 7 m ವ್ಯಾಸವನ್ನು ಹೊಂದಿರುವ ಒಂದು ಬಾವಿಯನ್ನು ತೋಡಿದೆ ಮತ್ತು ಭೂಮಿಯಿಂದ ತೆಗೆದ ಮಣ್ಣನ್ನು ಸಮವಾಗಿ ಹರಡಿ 22 m • 14 m ವೇದಿಕೆಯನ್ನು ಮಾಡಿದೆ. ವೇದಿಕೆಯ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

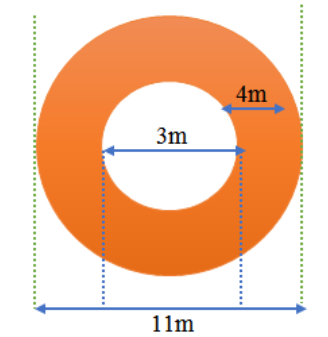
4. ಒಂದು ಬಾವಿಯ ವ್ಯಾಸ 3 m ಮತ್ತು ಆಳ 14 m ಇರುವಂತೆ ತೋಡಿದೆ. ಭೂಮಿಯಿಂದ ತೆಗೆದ ಮಣ್ಣನ್ನು ಬಾವಿಯ ಸುತ್ತಲು ಸಮವಾಗಿ ಹರಡಿ 4 m ಅಗಲವಿರುವ ವೃತ್ತಕಾರದ ಕಟ್ಟೆಯನ್ನು ಕಟ್ಟಿದೆ. ಕಟ್ಟೆಯ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

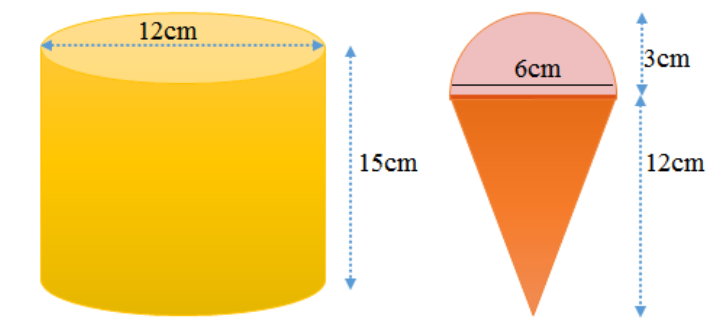
5. ಒಂದು ಪಾತ್ರೆಯು ನೇರ ವೃತ್ತ ಪಾದ ಸಿಲಿಂಡರಿನ ಆಕಾರದಲ್ಲಿದೆ. ಅದರ ವ್ಯಾಸ 12 cm ಮತ್ತು ಎತ್ತರ 15 cm ಇದ್ದು, ಅದರ ತುಂಬ ಐಸ್ಕ್ರೀಮ್ ಇದೆ. ಈ ಐಸ್ಕ್ರೀಮನ್ನು 12 cm ಎತ್ತರ ಮತ್ತು 6 cm ವ್ಯಾಸವಿರುವ ಶಂಕುವಿನಲ್ಲಿ, ಅದ ಮೇಲೆ ಒಂದು ಅರ್ಧಗೋಳವಿರುವಂತೆ ತುಂಬಬೇಕಾಗಿದೆ, ಈ ಐಸ್ಕ್ರೀಮನ್ನು ಎಷ್ಟು ಶಂಕುಗಳಲ್ಲಿ ತುಂಬಬಹುದು?
ಉತ್ತರ:
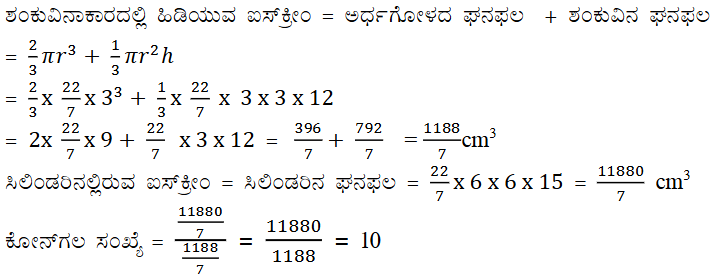
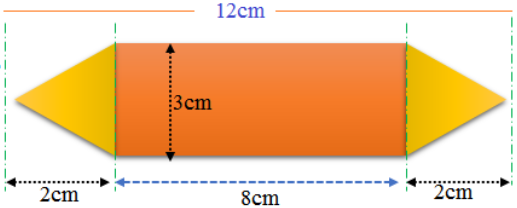
6. 1.75 cm ವ್ಯಾಸ ಹಾಗೂ 2 mm ದಪ್ಪ ಇರುವ ಬೆಳ್ಳಿ ನಾಣ್ಯಗಳಿವೆ. ಈ ನಾಣ್ಯಗಳನ್ನು ಕರಗಸಿ 5.5 cm x 10 cm x 3.5 cm ಅಳತೆಯ ಒಂದು ಆಯತ ಘನವನ್ನು ಮಾಡಬೇಕಾಗಿದೆ. ಹಾಗಾದರೆ ಎಷ್ಟು ಬೆಳ್ಳಿಯ ನಾಣ್ಯಗಳು ಬೇಕು?
ಉತ್ತರ:
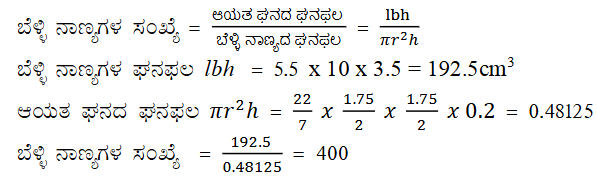
7. 32 cm ಎತ್ತರ ಮತ್ತು 18 cm ಪಾದದ ತ್ರಿಜ್ಯವಿರುವ ಒಂದು ಸಿಲಿಂಡರಿನಾಕಾರದ ಬಕೇಟ್ ನಲ್ಲಿ ಪೂರ್ಣವಾಗಿ ಮರಳನ್ನು ತುಂಬಿದೆ. ಬಕೇಟ್ನಲ್ಲಿರುವ ಮರಳನ್ನು ಪೂರ್ತಿಯಾಗಿ ನೆಲದ ಮೇಲೆ ಸುರಿದಾಗ ಅದು ಶಂಕುವಿನಾಕಾರದ ಮರಳಿನ ರಾಶಿಯನ್ನು ಉಂಟುಮಾಡಿದೆ. ಶಂಕುವಿನಾಕಾರದ ರಾಶಿಯ ಎತ್ತರವು 24 cm ಆದರೆ, ಮರಳಿನ ರಾಶಿಯ ತ್ರಿಜ್ಯ ಹಾಗೂ ಓರೆ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

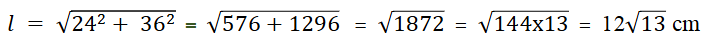
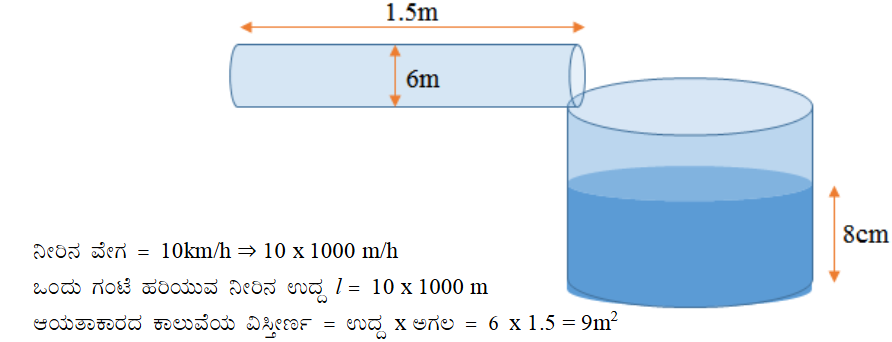
8. 6 m ಅಗಲ ಮತ್ತು 1.5 m ಆಳ ಇರುವ ಕಾಲುವೆಯಲ್ಲಿ ನೀರು 10 km/h ಜವದಲ್ಲಿ ಹರಿಯುತ್ತಿದೆ. 8 cm ನೀರು ನಿಲ್ಲುವ ಹಾಗೆ, 30 ನಿಮಿಷಗಳಲ್ಲಿ ಹರಿಯುವ ನೀರಿನಿಂದ ಎಷ್ಟು ಪ್ರದೇಶದ ವಿಸ್ತೀರ್ಣವನ್ನು ನೀರಾವರಿ ಮಾಡಬಹುದು?
ಉತ್ತರ:

9. 20 cm ಒಳ ವ್ಯಾಸವನ್ನು ಹೊಂದಿರುವ ಒಂದು ಕೊಳವೆಯನ್ನು ಬಳಸಿ, ಕಾಲುವೆಯಿಂದ ತನ್ನ ಹೊಲದಲ್ಲಿರುವ 10 m ವ್ಯಾಸ ಮತ್ತು 2 m ಆಳ ಇರುವ ಸಿಲಿಂಡರಿನಾಕಾರದ ತೊಟ್ಟಿಗೆ ಒಬ್ಬ ರೈತ ನೀರನ್ನು ಹರಿಸಿದ್ದಾನೆ. ಕೊಳವೆಯ ಮೂಲಕ ನೀರು 3 km/h ದರದಲ್ಲಿ ಹರಿದರೆ, ತೊಟ್ಟಿ ತುಂಬಲು ತೆಗೆದುಕೊಳ್ಳುವ ಅವಧಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

ಅಭ್ಯಾಸ 15.4
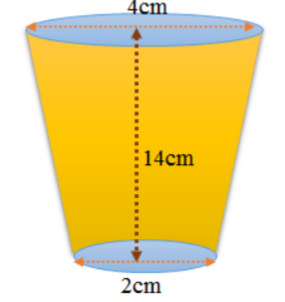
1. 14 cm ಎತ್ತರವಿರುವ ಒಂದು ಕುಡಿಯುವ ನೀರಿನ ಗಾಜಿನ ಲೋಟವು ಶಂಕುವಿನ ಭಿನ್ನಕದ ರೂಪದಲ್ಲಿದೆ. ಅದರ ಎರಡು ವೃತ್ತಾಕಾರದ ಪಾದಗಳ ವ್ಯಾಸಗಳು 4cm ಮತ್ತು 2cm ಗಳಾಗಿವೆ. ಗಾಜಿನ ಲೋಟದ ಸಾಮರ್ಥ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
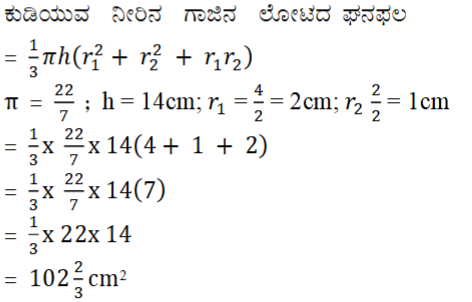
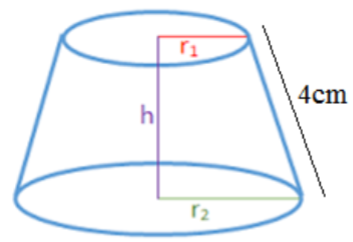
2. ಒಂದು ಶಂಕುವಿನ ಭಿನ್ನಕದ ಓರೆ ಎತ್ತರವು 4 cm ಮತ್ತು ಅದರ ವೃತ್ತಾಕಾರದ ಪಾದದ ಸುತ್ತಳತೆ (ಪರಿಧಿ)ಗಳು 18cm ಮತ್ತು 6cm ಶಂಕುವಿನ ಭಿನ್ನಕದ ಪಾರ್ಶ್ವ ಮೇಲೈ ವಿಸ್ತೀರ್ಣವನ್ನುಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
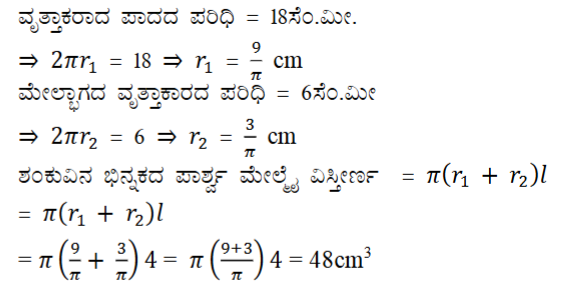
3. ಟರ್ಕಿ ದೇಶದ ಪ್ರಜೆಗಳು ಧರಿಸುವ ಟೋಪಿಗೆ ‘ಫೆಜ್’ ಎಂದು ಹೆಸರು. ಇದು ಶಂಕುವಿನ ಭಿನ್ನಕದ ರೂಪದಲ್ಲಿದೆ. (ಚಿತ್ರ 15.24 ನೋಡಿರಿ). ಅದರ ತೆರೆದ ಭಾಗದ ತ್ರಿಜ್ಯವು 10cm ಮತ್ತು ಮೇಲ್ಬಾಗದ ತ್ರಿಜ್ಯವು 4cm ಮತ್ತು ಅದರ ಓರೆ ಎತ್ತರವು 15cm ಆದರೆ ಅದನ್ನು ತಯಾರಿಸಲು ಉಪಯೋಗಿಸಿದ ವಸ್ತುವಿನ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
4. ಮೇಲ್ಬಾಗದಲ್ಲಿ ಮತ್ತು ತೆರೆದಿರುವ ಮತ್ತು ಒಂದು ಲೋಹದ ಹಾಳೆಯಿಂದ ಮಾಡಿದ ಒಂದು ಪಾತ್ರೆಯು ಶಂಕುವಿನ ಭಿನ್ನಕರ ಆಕಾರದಲ್ಲಿ ಇದೆ. ಶಂಕುವಿನ ಭಿನ್ನಕದ ಎತ್ತರ 16cm, ಅದರ ಕೆಳಭಾಗದ ಮತ್ತು ಮೇಲ್ಬಾಗದ ತ್ರಿಜ್ಯಗಳು 8cm ಮತ್ತು 20cm ಕ್ರಮವಾಗಿ ಇದೆ. ಈಪಾತ್ರೆಯನ್ನು ಹಾಲಿನಿಂದ ಸಂಪೂರ್ಣವಾಗಿ ತುಂಬಿಸಬೇಕಾಗಿದೆ. 1 ಲೀಟರ್ ಹಾಲಿನ ಬೆಲೆಯು ₹20 ರಂತೆ ಹಾಲನ್ನು ಕೊಳ್ಳಲು ಎಷ್ಟು ಹಣಬೇಕು? ಲೋಹದ ಹಾಳೆಯ ದರ ರೂ 8 ಪ್ರತಿ 100 cm² ಆದರೆ, ಇಡೀ ಪಾತ್ರೆಯನ್ನು ನಿರ್ಮಿಸಲು ಎಷ್ಟು ಹಣ ಬೇಕಾಗುತ್ತದೆ? ( π = 3.14 ಎಂದು ಪರಿಗಣಿಸಿ)
ಉತ್ತರ:



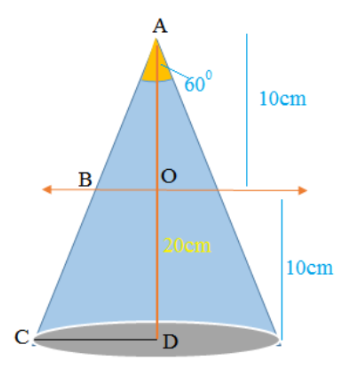
5. ಒಂದು ಲೋಹದಿಂದ ಮಾಡಿದ ವೃತ್ತಪಾದ ಶಂಕುವಿನ ಎತ್ತರ 20 cm ಮತ್ತು ಶೃಂಗ ಕೋನವು 600. ಈ ಶಂಕುವನ್ನು ಅದರ ಎತ್ತರದ ಮಧ್ಯಭಾಗದಲ್ಲಿ, ಪಾದಕ್ಕೆ ಸಮಾಂತರವಾಗಿ ಒಂದು ಸಮತಲದ ಮೂಲಕ ಕತ್ತರಿಸಿದೆ. ಈ ರೀತಿಯಾಗಿ ಪಡೆದ ಶಂಕುವಿನ ಭಿನ್ನಕವನ್ನು ತಂತಿಯ ವ್ಯಾಸ 1/16cm ಇರುವಂತೆ ತಂತಿಯಾಗಿ ಎಳೆದರೆ ತಂತಿಯ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
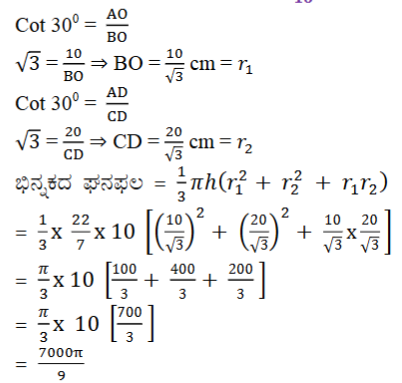

ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಆಂಶಗಳು
ಆಯತ ಘನ: ಹೊರ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ= 2h(I + b)
ಒಟ್ಟು ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2 (1b+nh + hl).
ಘನಫಲ- l b h, l: ಉದ್ದ, b: ಆಗಲ, h: ಎತ್ತರ
ರೂಮಿನ 4 ಗೋಡೆಗಳ ವಿಸ್ತೀರ್ಣ = lh + lh + bh + bh = 2(l + b)h
ಆಯತದ ಕರ್ಣ = √l2 + b2 + h2
ಚೌಕಘನ: ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 4a2
ಒಟ್ಟು ಮೇಲೆ ವಿಸ್ತೀರ್ಣ = 6a2
ಘನಫಲ = a3
ಚೌಕಘನ ಕರ್ಣ = √3a
ಮಾನಗಳ ಬದಲಾವಣೆಗಳು
ಉದ್ದದ ಮಾನಗಳು
(i) 2cm = 10mm
(ii) 1dm = 10cm = 100mm
(iii) 1m = 10 dm = 100cm
(iv) 1 dam = 10 m = 1000 cm
(v) 1 hm = 10 dam = 100 mp
(vi) 1 km = 1000 m = 100 dam = 10 hm
ವಿಸ್ತೀರ್ಣದ ಮಾನಗಳು
(vii) 1cm2 = 10mm x 10mm = 100 mm²
(viii) 1dm2 = 10cm x 10cm = 100cm2
(ix) 1m2 = 100cm x 100cm = 10000cm2
(x) Idam2 =10m x 10m = 100m²
(xi) 1hm2 = 100m x 100m = 10,000m2
(xii) 1km2 = 10hm x 10hm = 100hm 2
ಘನಫಲದ ಮಾನಗಳು
(xiii) 1cm³ = 1,000mm³, 1dm3 = 1000cm3
(xiv) Im3 = 1000dm3 x 1000cm litres
(xv) 1 litre = 1dm3 = 1000 litres
(xv) 1 litre = Idm3 = 1000cn3 = 3kL = 1000L = Im3
(xvi) ImL = lcm³
ಸಿಲಿಂಡರ್
ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2πvh
ಒಟ್ಟು ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2πr(r+h) = 2πrh + 2πr2
ಘನಫಲ = πr2h
r : ಪಾದದ ತ್ರಿಜ್ಯ ‘h’ ಎತ್ತರ
ಟೊಳ್ಳಾದ ಸಿಲಿಂಡರ್
ಸಿಲಿಂಡರ್ ದಪ್ಪ = R-r
ಅಡ್ಡ ವಿಭಾಗದ ಪ್ರದೇಶ = π(R² – r2)
ಬಾಹ್ಯ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2πRh
ಒಳ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2πrh
ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣ = ಹೊರ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ + ಒಳ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ + ಎರಡು ಬದಿಗಳ ವಿಸ್ತೀರ್ಣ. = 2πRh+ 2πrh+ 2π(R² – r²) = 2π(Rh+rh+R² – r²)
ವಸ್ತುವಿನ ಘನಫಲ = πR2h – πr2h = π(R² – r²)h
ಶಂಕು
ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = πrl = πr √(r2 + h2)
ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣ = ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ + ವೃತ್ತಪಾದದ ವಿಸ್ತೀರ್ಣ ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣ
= πrl + πr2 = πr(l + r)
ಘನಫಲ = 1/3 πr2h
ಓರೆ ಎತ್ತರ = l = √ (r2 + h2)
ಶಂಕುವಿನ ಭಿನ್ನಕ
ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = πl(R + r) where I = √(h2 + (R – r)2
ಒಟ್ಟು ಮೇಲೈ ವಿಸ್ತೀರ್ಣ = π{R2 + r2 + l(R + r)}
ಘನಫಲ = πh/3(R²+r²+Rr)
R ಮತ್ತು r : ತ್ರಿಜ್ಯಗಳು, h = ಎತ್ತರ l = ಓರೆ ಎತ್ತರ
ಗೋಳ
ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 4πr2
ಒಟ್ಟು ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ =4πr2
ಘನಫಲ = 4/3 πr3
r: ತ್ರಿಜ್ಯ
ಅರ್ಧಗೋಳ
ಪಾರ್ಶ್ವ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2πr2
ಒಟ್ಟು ಮೇಲ್ಮೈವಿಸ್ತೀರ್ಣ = 3πr2
ಘನಫಲ = 2/3πr3
r: ತ್ರಿಜ್ಯ
ಗೋಲಾಕಾರದ ಶೆಲ್
ದಪ್ಪ = R-r
ಘನಫಲ = 4/3 π(R3-r³)
R→ ಬಾಹ್ಯತ್ರಿಜ್ಯ r→ ಒಳತ್ರಿಜ್ಯ
ಅರ್ಧಗೋಲಾಕಾರದ ಶೆಲ್
ಪಾದದ ವಿಸ್ತೀರ್ಣ = π(R² – r2)
ಹೊರ ಮೇಲೈ ವಿಸ್ತೀರ್ಣ = 2πR²
ಒಳ ಮೇಲೈ ವಿಸ್ತೀರ್ಣ= 2πr²
ಒಟ್ಟು ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣ = 2πr² + 2πr² + π(R2 – r2) = π(3R2 – r2)
ವಸ್ತುವಿನ ಘನಫಲ = 2/3 π(R3 – r3)
ಇತರೆ ವಿಷಯಗಳು :
10ನೇ ತರಗತಿ ಗಣಿತ ಸಂಭವನೀಯತೆ ನೋಟ್ಸ್
10ನೇ ತರಗತಿ ಗಣಿತದಲ್ಲಿನ ಸಾಧನೆಗಳು ಗಣಿತ ನೋಟ್ಸ್
