10th Standard Ganitadallina Sadhanegalu Maths Notes Question and Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, 10ನೇ ತರಗತಿ ಗಣಿತ ಗಣಿತದಲ್ಲಿನ ಸಾಧನೆಗಳು ಗಣಿತ ನೋಟ್ಸ್̧, 10th Standard Ganitadallina Sadhanegalu Notes Question and Answer, 10th Standard Ganitadallina Sadhanegalu Notes, 10th Class Ganitadallina Sadhanegalu Maths Notes Pdf, 10th class maths notes pdf, 10th class all chapter maths notes in kannada medium, 10th standard maths notes, 10th Standard Ganitadallina Sadhanegalu Notes Question and Answer pdf.
ಅನುಬಂಧ A1
ಗಣಿತದಲ್ಲಿನ ಸಾಧನೆಗಳು
10ನೇ ತರಗತಿ ಗಣಿತದಲ್ಲಿನ ಸಾಧನೆಗಳು ನೋಟ್ಸ್
ಅಭ್ಯಾಸ A1.1
1. ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳು ಯಾವಾಗಲೂ ಸತ್ಯ, ಯಾವಾಗಲೂ ಮಿಥ್ಯ, ಅಥವಾ ಸಂದಿಗ್ಧದೇ ನಿರೂಪಿಸಿ ನಿಮ್ಮ ಉತ್ತರಗಳನ್ನು ಸಮರ್ಥಿಸಿ.
(i) ಎಲ್ಲಾ ಗಣಿತ ಪಠ್ಯಪುಸ್ತಕಗಳು ಆಸಕ್ತಿದಾಯಕವಾಗಿರುತ್ತವೆ.
(ii) ಭೂಮಿ ಮತ್ತು ಸೂರ್ಯನಿಗಿರುವ ಸರಿಸುಮಾರು ದೂರ 1.5×108 km.
(iii ) ಮನುಷ್ಯರೆಲ್ಲರಿಗೂ ವಯಸ್ಸಾಗುತ್ತದೆ.
(iv) ಉತ್ತರಕಾಶಿಯಿಂದ ಹರ್ಸಿಲ್ಗೆ ಪ್ರಯಾಣ ದಣಿವಾಗಿಸುತ್ತದೆ.
(v) ಮಹಿಳೆಯೊಬ್ಬರು ದ್ವಿನೇತ್ರಯಿಂದ ಆನೆಯೊಂದನ್ನು ನೋಡಿದರು.
ಉತ್ತರ:
(i) ಸಂದಿಗ್ಧ,
ಸಮರ್ಥನೆ: ಎಲ್ಲಾ ಗಣಿತ ಪಠ್ಯಪುಸ್ತಕಗಳು ಆಸಕ್ತಿದಾಯಕವಾಗಿರುತ್ತವೆಯೋ ಇಲ್ಲವೋ ಎಂದು ಹೇಳಲು ಸಾಧ್ಯವಿಲ್ಲ.
(ii) ಸರಿ,
ಸಮರ್ಥನೆ: ವಿಜ್ಞಾನಿಗಳು ಸಾಧಿಸಿ ತೋರಿಸುವಂತೆ ಭೂಮಿಯಿಂದ ಸೂರ್ಯನಿಗೆ ಇರುವ ದೂರ 149.6 ಮಿಲಿಯನ್ km ಅಥವಾ 1.5 x 108 km
(iii) ಸರಿ
ಕೆಲವು ವರ್ಷಗಳ ನಂತರ ಮನುಷ್ಯರೆಲ್ಲರಿಗೂ ವಯಸ್ಸಾಗುತ್ತದೆ.
(iv) ಸಂದಿಗ್ಧ,
ಕೆಲವು ಪ್ರಯಾಣಿಕರಿಗೆ ತಮ್ಮ ಪ್ರಯಾಣವು ಹರ್ಷದಾಯಕವಾಗಿರುತ್ತದೆ. ಮತ್ತು ಕೆಲವರಿಗೆ ಪ್ರಯಾಣ ದಣಿವಾಗಿಸುತ್ತದೆ.
(v) ಸಂದಿಗ್ಧ,
ಮಹಿಳೆಯೊಬ್ಬರು ದ್ವಿನೇತ್ರಯಿಂದ ಅಥವಾ ದುರ್ಬಿನಿನಿಂದ ಆನೆಯೊಂದನ್ನು ನೋಡಿದರು.
2. ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳು ಸರಿ ಅಥವಾ ತಪ್ಪಾಗಿದಿಯೇ ಎಂದು ತಿಳಿಸಿ. ನಿಮ್ಮ ಉತ್ತರವನ್ನು ಸಮರ್ಥಿಸಿ
(i) ಎಲ್ಲಾ ಪಡ್ಡುಜಾಕೃತಿಗಳು ಬಹುಭುಜಾಕೃತಿಗಳು.
(II) ಕೆಲವು ಬಹುಭುಜಾಕೃತಿಗಳು ಪಂಚಭುಜಾಕೃತಿಗಳು.
(iii) ಎಲ್ಲಾ ಸಮಸಂಖ್ಯೆಗಳು 2 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುವುದಿಲ್ಲ.
(iv) ಕೆಲವು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು.
(v) ಎಲ್ಲಾ ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳಲ್ಲ.
ಉತ್ತರ:̈
(i) ಸರಿ,
ಎಲ್ಲಾ ಷಡ್ಡುಜಾಕೃತಿಯ ಒಳಕೋನಗಳ ಮೊತ್ತ ಸಮವಾಗಿರುತ್ತದೆ.
(ii) ಸರಿ.
ಕೆಲವು ಬಹುಭುಜಾಕೃತಿಗಳು 5 ಬಾಹುಗಳನ್ನು ಒಳಗೊಂಡಿರುತ್ತವೆ.
(iii) ತಪ್ಪು,
ಎಲ್ಲಾ ಸಮಸಂಖ್ಯೆಗಳು 2 ರಿಂದ ಸಂಪೂರ್ಣವಾಗಿ ಭಾಗವಾಗಿ ಶೇಷ 0 ಯನ್ನು ಉಳಿಸುತ್ತದೆ.

ಉದಾಹರಣೆ:
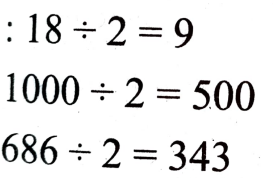
(iv) ಸರಿ,
ಕೆಲವು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳನ್ನು ಸಮರ್ಥಿಸಲು ಸಾಧ್ಯವಿಲ್ಲ.
ex: √7, √3, 2 + √3
(v) ಸರಿ
ಸಮರ್ಥನೆ: ಕೆಲವು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ಅಭಾಗಲಬ್ಬ ಸಂಖ್ಯೆಗಳು
3. a ಮತ್ತು b ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳಾಗಿದ್ದು ab ≠ 0 ಆಗಿದೆ. ಹಾಗಾದರೆ, ಈ ಕೆಳಗಿನ ಯಾವ ಹೇಳಿಕೆಗಳು ಸರಿ? ನಿಮ್ಮ ಉತ್ತರಗಳನ್ನು ಸಮರ್ಥಿಸಿ.
(i) a ಮತ್ತು b ಗಳೆರಡೂ ಸೊನ್ನೆಯಾಗಿರಬೇಕು.
(ii) a ಮತ್ತು b ಗಳೆರಡೂ ಸೊನ್ನೆಯಾಗಿರಬಾರದು.
(iii) a ಅಥವಾ b ಶೂನ್ಯವಲ್ಲದ ಸಂಖ್ಯೆಯಾಗಿರಬೇಕು.
ಉತ್ತರ:
(ii) a ಮತ್ತು b ಗಳೆರಡೂ ಸೊನ್ನೆಯಾಗಿರಬಾರದು.
4. ಸೂಕ್ತ ನಿಬಂಧನೆಗಳೊಂದಿಗೆ, ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳು ಸರಿಯಾಗುವಂತೆ ಪುನರ್ ನಿರೂಪಿಸಿ.
(i) a2 > b2, ಆದರೆ a > b
(ii) x2 = y2 ಆದರೆ x = y
(iii) (x + y)2 = x2 + y2 ಆದರೆ x = 0
(iv) ಚತುರ್ಭುಜದ ಕರ್ಣಗಳು ಪರಸ್ಪರ ದ್ವಿಭಾಗಿಸುತ್ತವೆ.
ಉತ್ತರ:
(i) a > 0 ಮತ್ತು a2 > b2 , a > b,
(ii) xy > 0 ಮತ್ತು x2 = y2 ಆದರೆ x = y.
(iii) (x + y)2 = x2 + y2 ಮತ್ತು y ≠ 0, ಆದರೆ x = 0
(iv) ಚತುರ್ಭುಜದ ಕರ್ಣಗಳು ಪರಸ್ಪರ ದ್ವಿಭಾಗಿಸುತ್ತವೆ.
ಅಭ್ಯಾಸ A1.2
1. ಎಲ್ಲಾ ಮಹಿಳೆಯರು ಸಾಯುತ್ತಾರೆ ಎಂದಾದರೆ ಮತ್ತು A ಒಬ್ಬ ಮಹಿಳೆ ಎಂದು ಭಾವಿಸಿದೆ. A ಯ ಬಗ್ಗೆ ನಾವು ಏನೆಂದು ತೀರ್ಮಾನಿಸಬಹುದು.
ಉತ್ತರ:
A ಮಹಿಳೆ ಸಾಯುತ್ತಾಳೆ
2. ಎರಡು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧವು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಮತ್ತು a ಮತ್ತು b ಗಳು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳಾಗಿದ್ದರೆ, ab ಯ ಬಗ್ಗೆ ನಿಮ್ಮ ತೀಮಾರ್ನವೇನು?
ಉತ್ತರ:
ab ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ
3. ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಗಳು ಅಂತ್ಯಗೊಳ್ಳದ, ಆವರ್ತವಾಗದ ಸಂಖ್ಯೆಗಳಾಗಿವೆ ಮತ್ತು √17 ಅಭಾಗಲಬ್ಧವಾದರೆ, √17 ರ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯ ಬಗ್ಗೆ ನಿಮ್ಮ ತೀರ್ಮಾನವೇನು?
ಉತ್ತರ:
√17ರ ದಶಮಾಂಶ ವಿಸ್ತರಣೆಯು ಅಂತ್ಯಗೊಳ್ಳದ ಮತ್ತು ಪುನರಾವರ್ತಿತವಲ್ಲದ ಸಂಖ್ಯೆ
√17 = 4.12310562562
4. y = x2 + 6 ಆಗಿದೆ ಮತ್ತು x = – 1 ಆದರೆ y ಬೆಲೆಯ ಬಗ್ಗೆ ನೀವು ಯಾವ ತೀರ್ಮಾನಕ್ಕೆ ಬರುವಿರೀ?
ಉತ್ತರ:
ಹೇಳಿಕೆಯಂತೆ
y = x2 + 6
x = – 1 ಆದಾಗ
y = (- 1)2 + 6
y = 1 + 6
y = 7
ಆದ್ದರಿಂದ y ನ ಬೆಲೆ 7.
5. ABCD ಸಮಾಂತರ ಚತುರ್ಭುಜ ಎಂದು ನೀಡಿದೆ ಮತ್ತು ∠B = 800 ಆದರೆ ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಉಳಿದ ಕೋನಗಳ ಬಗ್ಗೆ ನಿಮ್ಮ ತೀರ್ಮಾನವೇನು?
ಉತ್ತರ:
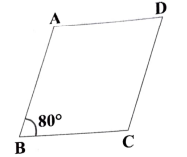
ABCD, ಸಮಾಂತರ ಚತುರ್ಭುಜದಲ್ಲಿ ಆಂತರಿಕ ಅನುಕ್ರಮ ಕೋನಗಳು ಮೊತ್ತ = 180°
∠A + ∠B = 1800
∠A = 180o – ∠B
= 180o – 80o
∠A = 100o
ಸಮಾಂತರ ಚತುರ್ಭುದಲ್ಲಿ ವಿರುದ್ಧ ಕೋನಗಳು ಸಮ
ಆದ್ದರಿಂದ ∠A = ∠C = 100o
∠B = ∠D = 80o
6. PQRS ಒಂದು ಚಕ್ರೀಯ ಚತುರ್ಭುಜವಾಗಿದೆ ಮತ್ತು ಅದರ ಕರ್ಣಗಳು ಪರಸ್ಪರ ದ್ವಿಭಾಗಿಸುತ್ತವೆ. ಚತುರ್ಭುಜದ ಬಗ್ಗೆ ನೀವು ಯಾವ ತೀರ್ಮಾನವನ್ನು ತೆಗೆದುಕೊಳ್ಳುವಿರಿ?
ಉತ್ತರ:
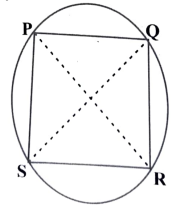
PQRS ಒಂದು ಆಯತ
ಏಕೆಂದರೆ
ಚಕ್ರೀಯ ಚತುರ್ಭುದ ಕರ್ಣಗಳು, ವೃತ್ತದಲ್ಲಿನ P,O,R ಮತ್ತು Sಗಳಿಂದ ಉಂಟಾದ ವ್ಯಾಸಗಳು.
7. ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ‘P’ ಗಳಿಗೆ P ಯು ಅಭಾಗಲಬ್ಧ ಮತ್ತು 3721 ಅವಿಭಾಜ್ಯ ಎಂದು ಭಾವಿಸಿದೆ. ನೀವು √3721 ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂಬ ತೀರ್ಮಾನಕ್ಕೆ ಬರಬಹುದೇ? ನಿಮ್ಮ ತೀರ್ಮಾನ ಸರಿಯಾಗಿದೆಯೇ? ಏಕೆ ಅಥವಾ ಆಗಿರುವುದಿಲ್ಲ.
ಉತ್ತರ:
ಹೌದು, ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಆಗಿರುವುದರಿಂದ ಇಲ್ಲ, ಏಕೆಂದರೆ √3721 = 61 ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ.
ಅಭ್ಯಾಸ A1.3
1. ಈ ಕೆಳಗಿನ ಪ್ರತಿ ಪ್ರಶ್ನೆಗಳಲ್ಲೂ ಒಂದು ಹೇಳಿಕೆಯನ್ನು ಸಾಧಿಸಲು ಕೇಳಿದ ಸಾಧನೆಯಲ್ಲಿನ ಎಲ್ಲಾ ಹಂತಗಳನ್ನು ಪಟ್ಟಿಮಾಡಿ, ಪ್ರತೀ ಹಂತಕ್ಕೂ ಕಾರಣ ನೀಡಿ.
1. ಎರಡೂ ಕ್ರಮಾನುಗತ ಬೆಸ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ 4 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
2. ಎರಡು ಕ್ರಮಾನುಗತ ಬೆಸ ಸಂಖ್ಯೆಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ. ಅವುಗಳ ವರ್ಗಗಳ ಮೊತ್ತ ಕಂಡುಹಿಡಿದು, ಫಲಿತಕ್ಕೆ 6 ನ್ನು ಸೇರಿಸಿ. ಈಗ ದೊರೆತ ಸಂಖ್ಯೆಯು 8 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
3. p>5 ಒಂದು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ, p2 + 2 ಇದು 3 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ ಎಂದು ತೋರಿಸಿ.
(ಸುಳುಹು: ಉದಾಹರಣೆ 11ನ್ನು ಉಪಯೋಗಿಸಿ)
4. x ಮತ್ತು y ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳಾಗಿರಲಿ. xy ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ತೋರಿಸಿ.
5. a ಮತ್ತು b ಧನ ಪೂರ್ಣಾಂಕಗಳಾಗಿದ್ದಾಗ, a = bq + r, 0 ≤ r < b, q ಒಂದು ಪೂರ್ಣಸಂಖ್ಯೆ ಆಗಿದೆ. ಮ.ಸಾ.ಅ (a, b) = ಮ. ಸಾ. ಅ (b,r) ಎಂದು ಸಾಧಿಸಿ.
(ಸುಳುಹು: ಮ. ಸಾ. ಅ (b,r) = h ಆಗಿರಲಿ. ಆಗ b = k1h ಮತ್ತು r = k2h ಇಲ್ಲಿ k1 ಮತ್ತು k1 ಸಹ ಅವಿಭಾಜ್ಯಗಳು)
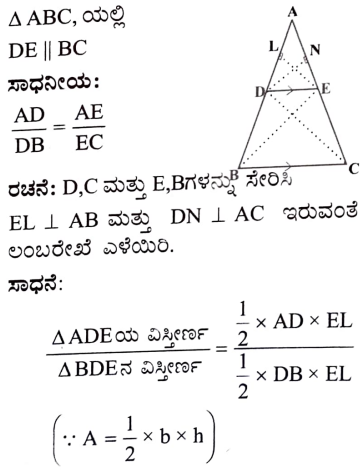
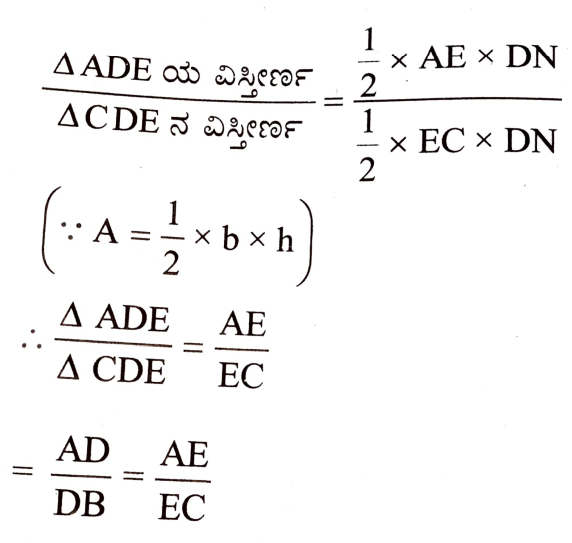
6. ΔABC ಯಲ್ಲಿ BC ಬಾಹುವಿಗೆ ಸಮಾಂತರವಾಗಿರುವ ರೇಖೆಯು AB ಮತ್ತು AC ಯನ್ನು ಕ್ರಮವಾಗಿ D ಮತ್ತು A ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಿದೆ AD/DB = AE/EC ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
1. ಎರಡು ಕ್ರಮಾನುಗತ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತವು 4 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
ಕ್ರಮಾನುಗತ ಬೆಸ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತಗಳನ್ನು ಗಮನಿಸಿ
11 +13 = 24
9 +11 = 20
25 + 27 = 52
101 + 103 = 204
ಮೊತ್ತವು 4 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ.
2n + 1 ಬೆಸಸಂಖ್ಯೆ
ಮುಂದಿನ ಬೆಸಸಂಖ್ಯೆ 2n + 3
(2n + 1) + (2n + 3)
= 4n + 4
= 4(n + 1)
4n + 4, ರ ಅಪವರ್ತನ 4
4n + 4, 4 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
ಎರಡೂ ಕ್ರಮಾನುಗತ ಬೆಸ ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ 4 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ.
2. ಎರಡು ಕ್ರಮಾನುಗತ ಬೆಸಸಂಖ್ಯೆಗಳು 13 ಮತ್ತು 15 ಆಗಿರಲಿ.
ಬೆಸಸಂಖ್ಯೆಗಳ ವರ್ಗ
132 + 152
169 + 225 = 394
ಬೆಸಸಂಖ್ಯೆಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ 6ನ್ನು ಕೂಡಿದಾಗ
394 + 6 = 400
400, 8 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ ಅಥವಾ (2n + 1) ಮತ್ತು (2n + 3) ಎರಡು ಕ್ರಮಾನುಗತ ಬೆಸಸಂಖ್ಯೆಗಳು ಅವುಗಳನ್ನು ವರ್ಗಗೊಳಿಸಿ ಕೂಡಿದಾಗ ಮೊತ್ತವು,
(2n + 1)2 + (2n + 3)2
= 4n2 + 4n + 1 + 4n2 + 4n + 9
= 8n2 + 8n + 10
ಮೊತ್ತಕ್ಕೆ 6ನ್ನು ಕೂಡಿದಾಗ
8n2 + 8n + 16
8 (n2 + n + 2) ಅಪವರ್ತನಗೊಳಿಸಿದಾಗ 8 n2 + n + 2ನ ಅಪವರ್ತನ ಅಂದರೆ n2 + n + 2 ನ್ನು 8 ಭಾಗಿಸುತ್ತದೆ.
3. ಯಾವುದೇ ಒಂದು ಧನ ಪೂರ್ಣಾಂಕ P = 5 ಆದರೆ P2 + 2 = 52 + 2 = 25 + 2 = 27
P = 7 ಆದರೆ P2 + 2 = 72 + 2 = 49 + 2 = 51
27 ಮತ್ತು 51 ಎರಡು 3ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
4. x ಮತ್ತು y ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳಾದರೆ, ಅವುಗಳನ್ನು x = a/b ಮತ್ತು y = c/d ಎಂದು ಬರೆಯಬಹುದು
ಆದ್ದರಿಂದ xy = (ac)/(bd) ಎರಡು ಪೂರ್ಣಾಂಕಗಳ ಗುಣಲಬ್ಬವು ಪೂರ್ಣಾಂಕವಾಗಿರುತ್ತದೆ.
ಆದ್ದರಿಂದ xy ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ
5. HCF (a, b) = h1
HCF (b, r) = h2
x/y ಅಂದರೆ x ನ್ನು ಭಾಗಿಸುತ್ತದೆ.
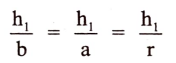
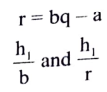
h2 ಮಹಾನ್ ಸಾಮಾನ್ಯ ಭಾಜಕ b ಮತ್ತು a ಗಳಿಗೆ
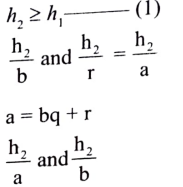
h1 ಮಹಾನ್ ಸಾಮಾನ್ಯ ಭಾಜಕ b ಮತ್ತು a ಗಳಿಗೆ
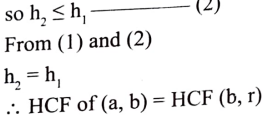
6.
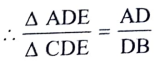
ಅಭ್ಯಾಸ A1.4
1. ಈ ಕೆಳಕಂಡ ಹೇಳಿಕೆಗಳ ನಕಾರೋಕ್ತಿಗಳನ್ನು ನಿರೂಪಿಸಿ.
(i) ಮನುಷ್ಯರೆಲ್ಲರೂ ಮರಣ ಹೊಂದುತ್ತಾರೆ.
(ii) ರೇಖೆ l ಇದು ರೇಖೆ m ಗೆ ಸಮಾಂತರವಾಗಿದೆ.
(iii) ಈ ಅಧ್ಯಾಯವು ಹಲವು ಅಭ್ಯಾಸಗಳನ್ನು ಹೊಂದಿದೆ.
(iv) ಎಲ್ಲಾ ಪೂರ್ಣಾಂಕಗಳು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು
(v) ಕೆಲವು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಬೆಸ ಸಂಖ್ಯೆಗಳು
(vi) ಯಾವುದೇ ವಿದ್ಯಾರ್ಥಿಯು ಸೋಮಾರಿಯಲ್ಲ
(vii) ಕೆಲವು ಬೆಕ್ಕುಗಳು ಕಪ್ಪಾಗಿಲ್ಲ
(viii) √x = -1 ಆಗಿರುವಂತೆ x ಎಂಬ ಯಾವುದೇ ವಾಸ್ತವ ಸಂಖ್ಯೆ ಇಲ್ಲ
(ix) 2 ಎಂಬ ಧನ ಪೂರ್ಣಾಂಕ a ಅನ್ನು ಭಾಗಿಸುತ್ತದೆ.
(x) a ಮತ್ತು b ಪೂರ್ಣಾಂಕಗಳು ಸಹ ಅವಿಭಾಜ್ಯಗಳು.
ಉತ್ತರ:
(i) ಮನುಷ್ಯರೆಲ್ಲರೂ ಮರಣ ಹೊಂದುವುದಿಲ್ಲ.
(ii) ರೇಖೆ l ಇದು ರೇಖೆ m ಸಮಾಂತರವಾಗಿಲ್ಲ.
(iii) ಈ ಅಧ್ಯಾಯವು ಹೆಚ್ಚು ಅಭ್ಯಾಸಗಳನ್ನು ಹೊಂದಿಲ್ಲ.
(iv) ಎಲ್ಲಾ ಪೂರ್ಣಾಂಕಗಳು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳಲ್ಲ.
(v) ಎಲ್ಲಾ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳು ಬೆಸ ಸಂಖ್ಯೆಗಳಲ್ಲ.
(vi) ಕೆಲವು ವಿದ್ಯಾರ್ಥಿಗಳು ಸೋಮಾರಿಗಳು.
(vii) ಎಲ್ಲಾ ಬೆಕ್ಕುಗಳು ಕಪ್ಪಾಗಿವೆ.
(viii) √x=-1 x ಎಂಬ ಯಾವುದೇ ವಾಸ್ತವ ಸಂಖ್ಯೆ ಇದೆ.
(ix) 2 ಎಂಬ ಧನ ಪೂರ್ಣಾಂಕ 4 ಅನ್ನು ಭಾಗಿಸುವುದಿಲ್ಲ.
(x) a ಮತ್ತು b ಪೂರ್ಣಾಂಕಗಳು ಸಹ ಅವಿಭಾಜ್ಯಗಳಲ್ಲ.
2. ಈ ಕೆಳಗಿನ ಪ್ರತಿ ಪ್ರಶ್ನೆಯಲ್ಲಿ ಎರಡು ಹೇಳಿಕೆಗಳಿವೆ. ಎರಡನೆಯ ಹೇಳಿಕೆಯು ಮೊದಲನೇ ಹೇಳಿಕೆಯ ನಕಾರೋಕ್ತಿ ಆಗಿದೆಯೇ ತಿಳಿಸಿ.
(1) ಮುಮ್ತಾಜ್ಗೆ ಹಸಿವಾಗಿದೆ
ಮುಮ್ತಾಜ್ಗೆ ಹಸಿವಾಗಿಲ್ಲ.
(ii) ಕೆಲವು ಬೆಕ್ಕುಗಳು ಕಪ್ಪಾಗಿವೆ.
ಕೆಲವು ಬೆಕ್ಕುಗಳು ಕಂದು ಬಣ್ಣದಲ್ಲಿವೆ.
(iii) ಎಲ್ಲಾ ಆನೆಗಳು ದೊಡ್ಡ ಗಾತ್ರದಲ್ಲಿವೆ.
ಒಂದು ಆನೆಯು ದೊಡ್ಡ ಗಾತ್ರದಲ್ಲಿವೆ.
(iv) ಎಲ್ಲಾ ಆಗ್ನಿ ಶಾಮಕ ವಾಹನಗಳು ಕೆಂಪು ಬಣ್ಣದಲ್ಲಿವೆ.
ಎಲ್ಲಾ ಆಗ್ನಿ ಶಾಮಕ ವಾಹನಗಳು ಕೆಂಪು ಬಣ್ಣದಲ್ಲಿಲ್ಲ.
(v) ಯಾವುದೇ ಮನುಷ್ಯ ಹಸುವಲ್ಲ
ಕೆಲವು ಮನುಷ್ಯರು ಹಸುಗಳು
ಉತ್ತರ:
(i) ಹೌದು
(ii) ಇಲ್ಲ
(iii) ಇಲ್ಲ
(iv) ಇಲ್ಲ
(v) ಹೌದು
ಅಭ್ಯಾಸ A1.5
1. ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳಿಗೆ ವಿಲೋಮಗಳನ್ನು ಬರೆಯಿರಿ:
(1) ಟೊಕಿಯಾದಲ್ಲಿ ತಾಪ ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಶರಣ್ ಹೆಚ್ಚು ಬೆವರುತ್ತಾರೆ.
(ii) ಶಾಲಿನಿಯವರಿಗೆ ಹಸಿವಾಗಿದ್ದರೆ, ಆಗ ಅವರ ಹೊಟ್ಟೆ ಚುರುಗುಟ್ಟುತ್ತದೆ.
(iii) ಜಸ್ವಂತ್ಗೆ ವಿದ್ಯಾರ್ಥಿವೇತನ ಸಿಕ್ಕಿದ್ದರೆ ಆಗ ಪದವಿ ಪಡೆಯಬಹುದು.
(iv) ಒಂದು ಗಿಡವು ಹೂಗಳನ್ನು ಹೊಂದಿದ್ದರೆ ಆಗ ಅದು ಜೀವಂತವಾಗಿದೆ.
(v) ಒಂದು ಪ್ರಾಣಿಯು ಬೆಕ್ಕು ಆಗಿದ್ದರೆ ಆಗ ಅದಕ್ಕೆ ಬಾಲವಿರುತ್ತದೆ.
ಉತ್ತರ:
(i) ಶರಣ್ ಹೆಚ್ಚು ಬೆವರುತ್ತಾರೆ ಎಂದರೆ ಟೊಕಿಯಲ್ಲಿ ತಾಪ ಹೆಚ್ಚಾಗಿದೆ.
(ii) ಶಾಲಿನಿಯವರಿಗೆ ಹೊಟ್ಟೆ ಚುರುಗುಟ್ಟಿದರೆ ಹಸಿವಾಗಿದೆ ಎಂದರ್ಥ.
(iii) ಜಸ್ವಂತ್ನ್ನು ಪದವಿ ಪಡೆಯಲು ವಿದ್ಯಾರ್ಥಿವೇತನ ಸಿಗಬೇಕು.
(iv) ಒಂದು ಗಿಡವು ಜೀವಂತವಾಗಿದ್ದರೆ ಅದು ಹೂಗಳನ್ನು ಬಿಡುತ್ತದೆ.
(v) ಒಂದು ಪ್ರಾಣಿಗೆ ಬಾಲವಿದ್ದರೆ ಅದು ಬೆಕ್ಕು ಆಗಿರುತ್ತದೆ.
2. ಈ ಕೆಳಗಿನ ಹೇಳಿಕೆಗಳ ವಿಲೋಮಗಳನ್ನು ಬರೆಯಿರಿ ಪ್ರತಿ ಸಂದರ್ಭದಲ್ಲಿಯೂ ವಿಲೋಮವು ಸರಿ ಅಥವಾ ತಪ್ಪಾಗಿದೆಯೇ ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸಿ.
(i) ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜವಾಗಿದ್ದರೆ ಆಗ ಪಾದಕೋನಗಳು ಸಮ
(ii) ಪೂರ್ಣಾಂಕವೊಂದು ಬೆಸ ಸಂಖ್ಯೆಯಾದರೆ, ಅದರ ವರ್ಗವು ಬೆಸ ಪೂರ್ಣಾಂಕದೇ ಆಗಿರುತ್ತದೆ.
(iii) x2 = 1, ಆಗಿದ್ದರೆ x = 1
(iv) ABCD ಸಮಾಂತರ ಚತುರ್ಭುಜವಾಗಿದ್ದರೆ, AC ಮತ್ತು BD ಪರಸ್ಪರ ದ್ವಿಭಾಗಿಸುತ್ತದೆ.
(V) a, b ಮತ್ತು C ಗಳು ಪೂರ್ಣಾ ಸಂಖ್ಯೆಗಳಾಗಿದ್ದರೆ, ಆಗ, a + (b + c) = (a + b) + c
(vi) x ಮತ್ತು y ಬೆಸ ಸಂಖ್ಯೆಗಳಾಗಿದ್ದರೆ, x + y ಒಂದು ಸಮ ಸಂಖ್ಯೆ
(vii) ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಶೃಂಗಗಳು ವೃತ್ತದ ಮೇಲಿದ್ದರೆ ಅದು ಆಯತವಾಗಿತ್ತದೆ.
ಉತ್ತರ:
(i) ತ್ರಿಭುಜ ABC ಯ ಪಾದ ಕೋನಗಳು ಸಮಾನಾಗಿದ್ದರೆ ಅದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜ. ಆದ್ದರಿಂದ ಕೊಟ್ಟಿರುವ ಹೇಳಿಕೆ ಸರಿ.
(ii) ಯಾವುದೇ ಒಂದು ಪೂರ್ಣಾಂಕದ ವರ್ಗವು ಬೆಸಸಂಖ್ಯೆ ಆಗಿದ್ದರೆ ಆ ಪೂರ್ಣಾಂಕವು ಬೆಸ ಸಂಖ್ಯೆ.
ಉದಾ: 52 = 25
(iii) x = 1 ಆದರೆ x2 = 1 ಕೊಟ್ಟಿರುವ ಹೇಳಿಕೆ ಸರಿ.
(iv) AC ಮತ್ತು BD ಗಳು ಒಂದಕ್ಕೊಂದು ಛೇದಿಸಿದರೆ ABCD ಸಮಾಂತರ ಚತುರ್ಭುಜ, ಕೊಟ್ಟಿರುವ ಹೇಳಿಕೆ ಸರಿ.
(v) a + (b + c) = (a + b) + c ಆದರೆ a, b ಮತ್ತು ಪೂರ್ಣಾಂಕ ಸಂಖ್ಯೆಗಳು,
(vi) x + y ಸಮ ಸಂಖ್ಯೆಯಾದರೆ x ಮತ್ತು y ಗಳು ಬೆಸಸಂಖ್ಯೆಗಳು ಕೊಟ್ಟಿರುವ ಹೇಳಿಕೆ ತಪ್ಪು,
(vii) ಸಮಾಂತರ ಚತುರ್ಭುಜವು ಆಯತವಾಗಬೇಕಾದರೆ ಶೃಂಗಬಿಂದುಗಳು ವೃತ್ತದ ಮೇಲಿರಬೇಕು.
ಅಭ್ಯಾಸ A1.6
1. a + b = c + d ಮತ್ತು a < c ಎಂದು ಭಾವಿಸಿ. ವೈರುಧ್ಯದಿಂದ ಸಾಧನೆ ಬಳಸಿ b > d ಎಂದು ತೋರಿಸಿ.
ಉತ್ತರ:
a = 3, b = a, c = 7, d = 5 ಆಗಿರಲಿ
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ a + b = c + d
3 + 9 = 7 + 5
12 = 12
a < c ಮತ್ತು b > d
2. r ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಮತ್ತು X ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯಾಗಿರಲಿ, ವೈರುಧ್ಯದಿಂದ ಸಾಧನೆ ವಿಧಾನ ಬಳಸಿ. r + x ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ತೋರಿಸಿ,
ಉತ್ತರ:
ಹೇಳಿಕೆಯಂತೆ : r ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ. ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ
r + x ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಸಾಧಿಸಿ.
ಸಾಧನೆ: r + x ಒಂದು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ತೆಗೆದುಕೊಳ್ಳಿ.
r ಒಂದು ಭಾಗಲಬ್ಧ – r ಕೂಡ ಒಂದು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯಾದರೆ r +x ಮೊತ್ತ, ಮತ್ತು -r ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ (r + x) + (- r) = x ಒಂದು ಭಾಗಲಬ್ಧ
X ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂಬ ನಮ್ಮ ಊಹೆ ತಪ್ಪು.
r + x ಒಂದು ಭಾಗಲಬ್ಧ.
3. ಯಾವುದೇ ಪೂರ್ಣಾಂಕ a ಗೆ a² ಸಮಸಂಖ್ಯೆ ಆದರೆ ಚಿ ಯು ಸಮ ಸಂಖ್ಯೆ ಎಂದು ವೈರುಧ್ಯದಿಂದ ಸಾಧಿಸಿ.
(ಸುಳುವು: a ಯು ಸಮಸಂಖ್ಯೆಯಲ್ಲ ಎಂದು ಭಾವಿಸಿ. ಅಂದರೆ ಇದು 2n + 1 ರೂಪದಲ್ಲಿದೆ, ಇಲ್ಲಿ n ಒಂದು ಪೂರ್ಣಾಂಕ ಎಂದು ಮುಂದುವರಿಯಿರಿ).
ಉತ್ತರ:
a2 ಒಂದು ಸಮಸಂಖ್ಯೆ ಆದರೆ ‘a’ ಕೂಡ ಸಮಸಂಖ್ಯೆ
a ಸಮಸಂಖ್ಯೆ ಆದರೆ a2 ಕೂಡ ಸಮಸಂಖ್ಯೆ
ಅದನ್ನು ಈ ರೀತಿ ಪ್ರತಿಪಾದಿಸಬಹುದು,
a2 = 2k ಆದರೆ
a2 = 4k2
a2 = 2(2k2) ಸಮಸಂಖ್ಯೆ
4. ಯಾವುದೇ ಪೂರ್ಣಾಂಕ a ಗೆ a2 ಇದು 3 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ ಆಗ a ಯು 3 ರಿಂದ ಭಾಗವಾಗುತ್ತದೆ ಎಂದು ವೈರುಧ್ಯದಿಂದ ಸಾಧಿಸಿ.
ಉತ್ತರ:
a ಒಂದು ಪೂರ್ಣಾಂಕ a2, 3 ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
k, ಒಂದು ಪೂರ್ಣಾಂಕವಾದರೆ ಮತ್ತು a ಒಂದು ಪೂರ್ಣಾಂಕವಾದರೆ n, ದಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
a = n(k + 1)
a = nk + n
a2 = (nk + n)(nk + n)
a2 = n(k + 1) n(k + 1)
a2 = n2 (k + 1) (k + 1)
ಆದ್ದರಿಂದ n ನಿಂದ a2 ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ,
3 ರಿಂದ a ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
3 ರಿಂದ a2 ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ.
5. 6n ದ ವಿಸ್ತಾರದಲ್ಲಿ ‘n’ ಯಾವುದೇ ಬೆಲೆಗೆ ಸೊನ್ನೆಯಿಂದ ವೈರುಧ್ಯದಿಂದ ಸಾಧಿಸಿ. ಅಂತ್ಯವಾಗುವುದಿಲ್ಲವೆಂದು ವೈರುಧ್ಯದಿಂದ ಸಾಧಿಸಿ.
ಉತ್ತರ:
ಯಾವುದೇ ಸಂಖ್ಯೆಯು ಸೊನ್ನೆಯಿಂದ ಅಂತ್ಯವಾದರೆ ಅದು 2 ಮತ್ತು 5ರಿಂದ ಭಾಗಿಸಲ್ಪಡುತ್ತವೆ.
2ರಿಂದ 6 ಭಾಗಿಸಲ್ಪಡುತ್ತದೆ ಆದರೆ 5 ರಿಂದ 6 ಭಾಗಿಸಲ್ಪಡುವುದಿಲ್ಲ ಆದ್ದರಿಂದ 6n ಸೊನ್ನೆಯಿಂದ ಅಂತ್ಯಗೊಳ್ಳುವುದಿಲ್ಲ.
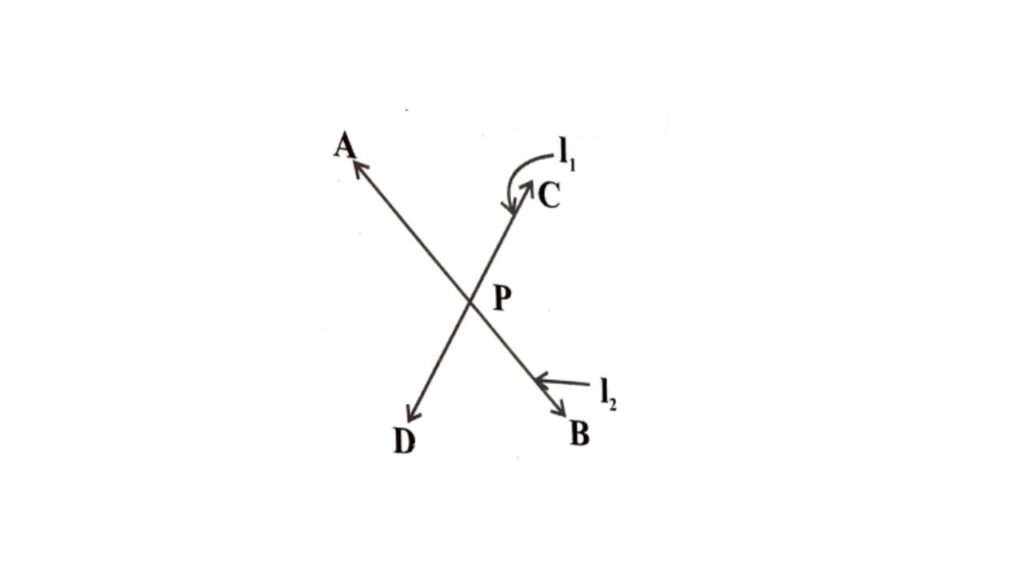
6. ಒಂದೇ ಸಮತಲದಲ್ಲಿನ ಯಾವುದೇ ಎರಡು ವಿಭಿನ್ನ ರೇಖೆಗಳು ಒಂದಕ್ಕಿಂತ ಹೆಚ್ಚು ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವುದಿಲ್ಲವೆಂದು ವೈರುಧ್ಯದಿಂದ ಸಾಧಿಸಿ.
ಉತ್ತರ:
ಎರಡು ವಿಭಿನ್ನ ರೇಖೆಗಳು ಯಾವಾಗಲೂ ಒಂದೊಂದನ್ನು ಕೇಲವ ಒಂದಿ ಬಿಂದುವಿನಲ್ಲಿ ಛೇಧಿಸುತ್ತದೆ. l1 ಮತ್ತು l2 ಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿರುವ ಎರಡು ರೇಖೆಗಳು P ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ.
ನೆನಪಿನಲ್ಲಿಡಬೇಕಾದ ಅಂಶಗಳು
ಆದೇಶವಲ್ಲದ, ಆಶ್ಚರ್ಯ ಸೂಚಕ ಅಥವಾ ಪ್ರಶ್ನಾರ್ಥಕವಲ್ಲದ ಒಂದು ಅರ್ಥ ಪೂರ್ಣ ವಾಕ್ಯವೇ ಹೇಳಿಕೆ. ಸಾಮಾನ್ಯವಾಗಿ ಹೇಳಿಕೆಗಳು ಈ ಕೆಳಗಿನವುಗಳಲ್ಲಿ ಯಾವುದಾದರೊಂದು ಆಗಿರಬಹುದು.
ಯಾವಾಗಲೂ ಸತ್ಯ, ಯಾವಾಗಲೂ ಮಿಥ್ಯ, ಸಂದಿಗ್ಧ (ಗೊಂದಲ).
ಇತರೆ ವಿಷಯಗಳು :
ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣಗಳು ಮತ್ತು ಘನಫಲಗಳು ನೋಟ್ಸ್
