10th Class Tribujagalu Maths Notes Question Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, ತ್ರಿಭುಜಗಳು notes 10th standard, 10th ಗಣಿತ ನೋಟ್ಸ್, ತ್ರಿಭುಜಗಳು 10ನೇ ತರಗತಿ, 10th Standard Samantara Shredigalu Question and Answer, 10th maths notes pdf kannada medium Part – 1, 10th standard triangle notes in kannada medium, 10ನೇ ತರಗತಿ ಗಣಿತ ತ್ರಿಭುಜಗಳು ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು, ತ್ರಿಭುಜಗಳು 10ನೇ ತರಗತಿ ಪ್ರಮೇಯ, class 10th tribhujagalu prameya kannada, tribujagalu in kannada 10th class important questions, 10th maths triangles exercise 2.3 solutions in kannada, kseeb solutions for class 10 maths in kannada chapter 2 Notes, 10th class maths 2nd chapter important questions formulas, 10th standard maths 2nd chapter notes, 10th maths 2nd lesson important questions in kannada medium.
ಘಟಕ 02 – ತ್ರಿಭುಜಗಳು
10ನೇ ತರಗತಿ ಗಣಿತ ತ್ರಿಭುಜಗಳು ನೋಟ್ಸ್
ಅಭ್ಯಾಸ 2.1
1. ಅವರಣದಲ್ಲಿ ಕೊಟ್ಟಿರುವ ಪದಗಳಿಂದ ಸೂಕ್ತವಾದ ಪದವನ್ನು ಆರಿಸಿ ಬಿಟ್ಟ ಪದ ತುಂಬಿಸಿ
i) ಎಲ್ಲಾ ವೃತ್ತಗಳು_______________ (ಸರ್ವಸಮ, ಸಮರೂಪ)
ii) ಎಲ್ಲಾ ವರ್ಗಗಳು_________________(ಸಮರೂಪ, ಸರ್ವಸಮ)
iii) ತ್ರಿಭುಜಗಳು ಸಮರೂಪ___________ (ಸಮದ್ವಿಬಾಹು, ಸಮಬಾಹು)
iv) ಬಾಹುಗಳ ಸಂಖ್ಯೆ ಒಂದೇ ಇರುವ ಎರಡು ಬಹುಭುಜಾಕೃತಿಗಳು ಸಮರೂಪವಾಗಬೇಕಾದರೆ
a) ಅದರ ಅನುರೂಪ ಕೋನಗಳು ____________________ ಮತ್ತು
b) ಅದರ ಅನುರೂಪ ಬಾಹುಗಳು ________________ (ಸಮ, ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ)
ಉತ್ತರ :
i) ಸಮರೂಪ
ii) ಸಮರೂಪ
iii) ಸಮರೂಪ
iv) ಸಮ, ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ
2. ಎರಡು ವಿಭಿನ್ನ ಉದಾಹರಣೆಗಳನ್ನು ಕೊಡಿ
i) ಒಂದು ಜೊತೆ ಸಮರೂಪ ಆಕೃತಿಗಳು
ಉತ್ತರ:
a) ಎರಡು ಸಮಬಾಹು ತ್ರಿಭುಜಗಳು
b) ಒಬ್ಬ ವ್ಯಕ್ತಿಯ ಒಂದೇ ತರಹದ ಬೇರೆ ಅಳತೆಯ ಭಾವಚಿತ್ರ
ii) ಒಂದು ಜೊತೆ ಸಮರೂಪವಲ್ಲದ ಆಕೃತಿಗಳು
a) ವೃತ್ತ ಮತ್ತು ಚೌಕ
b) ಒಬ್ಬ ವ್ಯಕ್ತಿಯ ಬೇರೆ ಬೇರೆ ಭಂಗೀಯಿಂದ ಕೂಡಿದ ಎರಡು ಬೇರೆ ಅಳತೆಯ ಭಾವಚಿತ್ರ
3. ಕೆಳಗಿನ ಚತುರ್ಭುಜಗಳು ಸಮರೂಪವೇ? ಇಲ್ಲವೆ ತಿಳಿಸಿ.
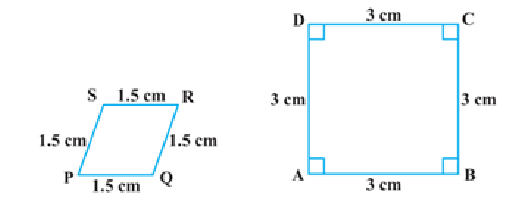
ಉತ್ತರ: ಚತುರ್ಭುಜಗಳು ಸಮರೂಪಿಗಳಲ್ಲ, ಏಕೆಂದರೆ ಅವುಗಳ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾಗಿಲ್ಲ
ಅಭ್ಯಾಸ 2.2
1). ಚಿತ್ರ 2.17 ರ (i) ಮತ್ತು (ii) ರಲ್ಲಿ DE||BC ಆದರೆ (i) ರಲ್ಲಿ EC (ii) ರಲ್ಲಿ AD ಕಂಡುಹಿಡಿಯಿರಿ.
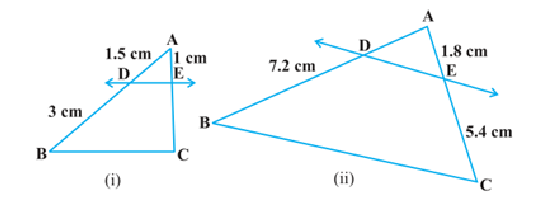
ಉತ್ತರ:

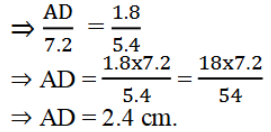
2. E ಮತ್ತು F ಬಿಂದುಗಳು ಕ್ರಮವಾಗಿ ∆PQR ನ PQ ಮತ್ತು PR ಗಳ ಮೇಲಿನ ಬಿಂದುಗಳು. ಕೆಳಗಿನ ಪ್ರತಿ ಸಂದರ್ಭಗಳಲ್ಲಿ EF|| QR ಆಗಿದೆಯೇ ಪರೀಕ್ಷಿಸಿ.
(i) PE = 3.9cm EQ = 3cm PF = 3.6cm FR = 2.4cm
(ii) PE = 4cm QE = 4.5cm PF = 8cm RF = 9cm
(iii) PQ = 1.28cm PR 2.56cm PE 0.18cm PF = 0.36cm
ಉತ್ತರ:



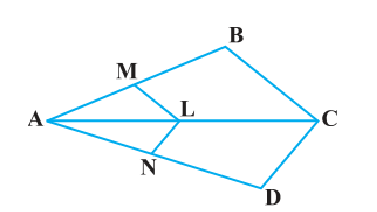
ಉತ್ತರ:

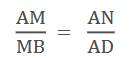
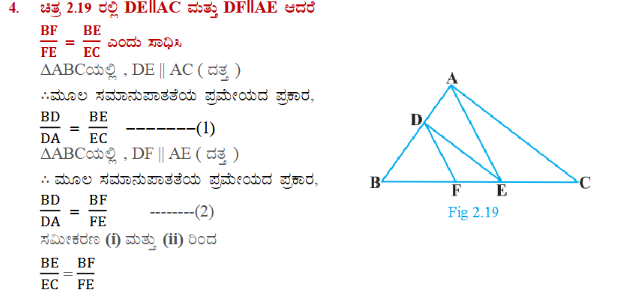
5). ಚಿತ್ರ 2.20 ಯಲ್ಲಿ DE || OQ ಮತ್ತು DF || OR ಆದರೆ EF || QR ಎಂದು ಸಾಧಿಸಿ.
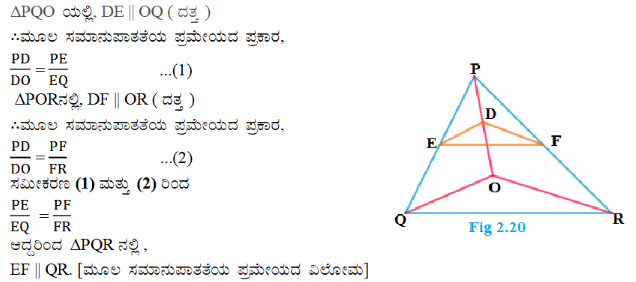
6). ಚಿತ್ರ 2.21 ರಲ್ಲಿ AB || PQ ಮತ್ತು AC || PR ಆಗುವಂತೆ A, B ಮತ್ತು C ಗಳು ಕ್ರಮವಾಗಿ OP, OQ ಮತ್ತು QR ಗಳ ಚಿತ್ರ 2.20 ಮೇಲಿನ ಬಿಂದುಗಳು. ಆದರೆ BC || QR ಎಂದು ತೋರಿಸಿ.
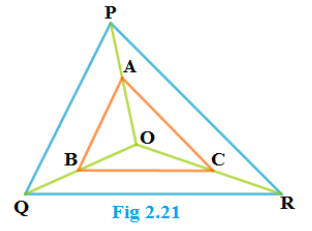
ಉತ್ತರ:

ಆದ್ದರಿಂದ, ΔOQR ನಲ್ಲಿ, BC || QR ( ಮೂಲ ಸಮಾನುಪಾತತೆಯ ಪ್ರಮೇಯದ ವಿಲೋಮ)
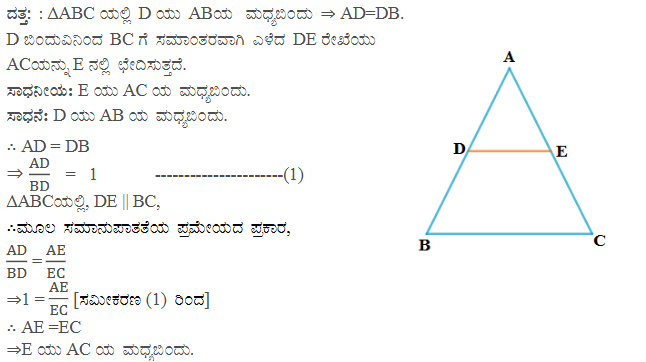
7. ತಿಭುಜದ ಒಂದು ಬಾಹುವಿನ ಮಧ್ಯಬಿಂದುವಿನಿಂದ ಮತ್ತೊಂದು ಬಾಹುವಿಗೆ ಸಮಾನಾಂತರವಾಗಿ ಎಳೆದ ಸರಳರೇಖೆಯು ಅದರ ಮೂರನೇ ಬಾಹುವನ್ನು ಅರ್ಧಿಸುತ್ತದೆ ಎಂದು ಪ್ರಮೇಯ 2.1 ನ್ನು ಉಪಯೋಗಿಸಿ ಸಾಧಿಸಿ (ನೀವು ಇದನ್ನು 9ನೇ ತರಗತಿಯಲ್ಲಿ ಸಾಧಿಸಿದ್ದೀರಿ ಎಂಬುವುದನ್ನು ಜ್ಞಾಪಿಸಿಕೊಳ್ಳಿ).
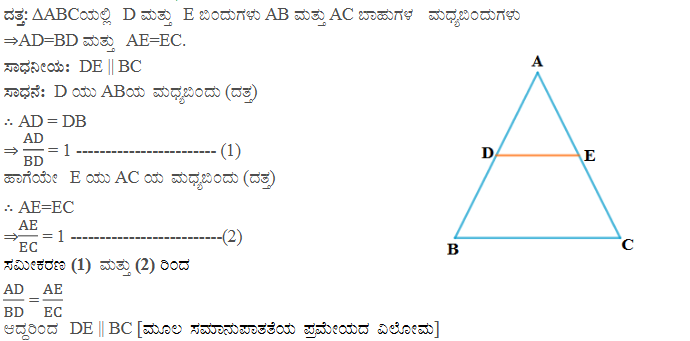
8). ತ್ರಿಭುಜದ ಯಾವುದಾದರೂ ಎರಡು ಬಾಹುಗಳ ಮದ್ಯ ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖೆಯು ಮೂರನೇ ಬಾಹುವಿಗೆ ಸಮಾಂತರವಾಗಿರುತ್ತದೆ ಎಂದು ಪ್ರಮೇಯ 2.2 ನ್ನು ಉಪಯೋಗಿಸಿ ಸಾಧಿಸಿ (ನೀವು ಇದನ್ನು 9ನೇ ತರಗತಿಯಲ್ಲಿ ಕಲಿತಿರುವಿರಿ ಎಂಬುವುದನ್ನು ಜ್ಞಾಪಿಸಿಕೊಳ್ಳಿ).


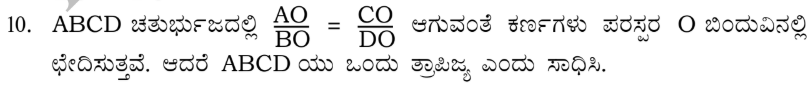
ಅಭ್ಯಾಸ 2.3
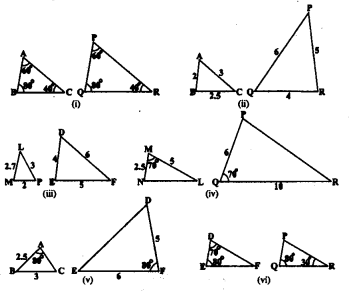
1). ಚಿತ್ರ 2.34 ರಲ್ಲಿ ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ಜೊತೆಗಳು ಯಾವುವು ತಿಳಿಸಿ. ಈ ಪ್ರಶ್ನೆಗಳನ್ನು ಉತ್ತರಿಸಲು ಸಮರೂಪತೆಯ ಯಾವ ನಿರ್ಧಾರಕ ಗುಣಗಳನ್ನು ಉಪಯೋಗಿಸಿರುವಿರಿ ಎಂದು ಬರೆಯಿರಿ ಹಾಗೂ ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ಜೊತೆಗಳನ್ನು ಸೂಚಿಸಲು ಸಂಕೇತವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
i) ΔABC ಮತ್ತು ΔPQR ಗಳಲ್ಲಿ
∠A = ∠P = 60° ( ದತ್ತ )
∠B = ∠Q = 80° ( ದತ್ತ )
∠C = ∠R = 40° ( ದತ್ತ )
∴ ΔABC ~ ΔPQR (AAA ಸಮರೂಪತೆ ನಿರ್ಧಾರಕ ಗುಣ)





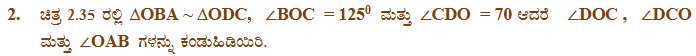
ಉತ್ತರ:


ಉತ್ತರ:

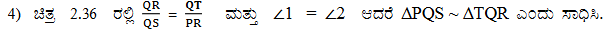
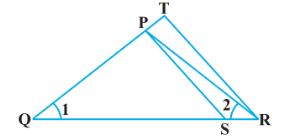
ಉತ್ತರ:


5. ∠P = ∠RTS ಆಗಿರುವಂತೆ S ಮತ್ತು T ಗಳು ∆PQR ನ PR ಮತ್ತು QR ಬಾಹುಗಳ ಮೇಲಿನ ಬಿಂದುಗಳು ಆದರೆ ∆RPQ ~ ∆RTS ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
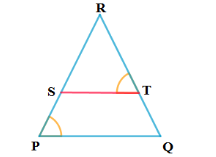

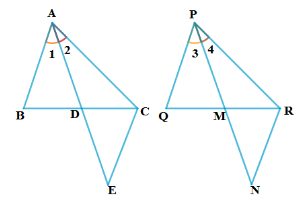
6. ಚಿತ್ರ 2.37 ∆ABE ≅ ∆ACD ರಲ್ಲಿ ಆದರೆ ∆ADE ~ ∆ABC ಎಂದು ಸಾಧಿಸಿ.
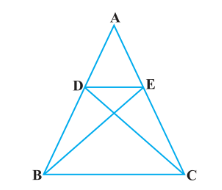
ಉತ್ತರ:

7. ಚಿತ್ರ 2.38 ರಲ್ಲಿ ∆ABC ಯ ಎತ್ತರಗಳಾದ AD ಮತ್ತು CE ಗಳು ಪರಸ್ಪರ P ನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ. ಆದರೆ
i) ∆AEP ~ ∆CDP
ii) ∆ABD ~ ∆CBE
iii) ∆AEP ~ ∆ADB
iv) ∆PDC ~ ∆BEC ಎಂದು ಸಾಧಿಸಿ.
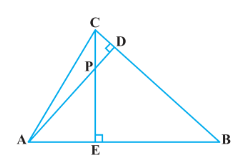
ಉತ್ತರ:


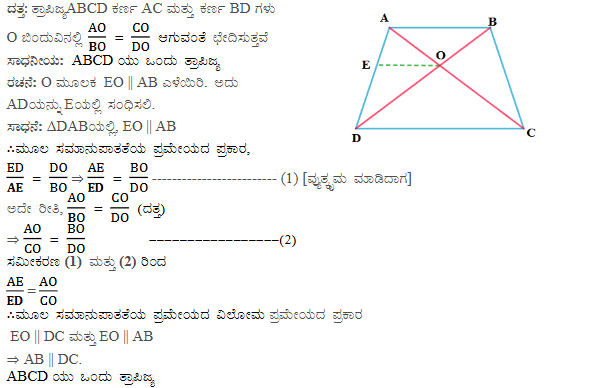
8). ABCD ಸಮಾಂತರ ಚತುರ್ಭುಜದ AD ಬಾಹುವನ್ನು ವೃದ್ಧಿಸಿದ ಭಾಗದಲ್ಲಿ E ಬಿಂದುವಿದೆ ಮತ್ತು BE ಮತ್ತು CD ಗಳು ಪರಸ್ಪರ ಈ ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಿದರೆ ∆ABE ~ ∆CFB ಎಂದು ಸಾಧಿಸಿ.
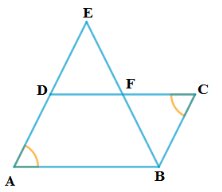
ಉತ್ತರ:

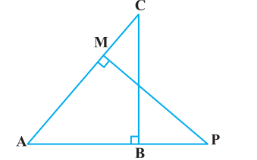
9. ಚಿತ್ರ 2.39 ರಲ್ಲಿ ∆ABC ಮತ್ತು ∆AMP ಗಳು ಕ್ರಮವಾಗಿ B ಮತ್ತು M ಗಳಲ್ಲಿ ಲಂಬ ಕೋನಗಳನ್ನು ಹೊಂದಿರುವ ಲಂಬಕೋನ ತ್ರಿಭುಜಗಳು ಆದರೆ:
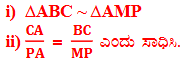
ಉತ್ತರ:

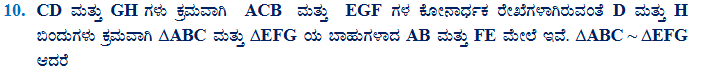
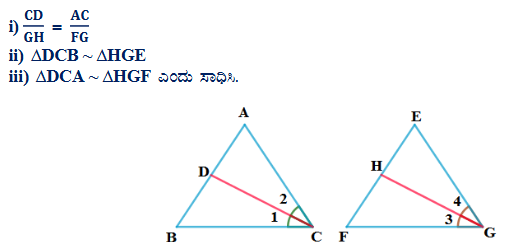
ಉತ್ತರ:



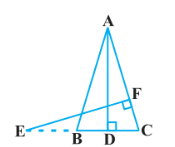
11. ಚಿತ್ರ 2.40 ಯಲ್ಲಿ ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ AB = AC, E ಯು CB ಯನ್ನು ವೃದ್ಧಿಸಿದ ರೇಖೆಯ ಮೇಲಿನ ಒಂದು ಬಿಂದು AD⟘BC, EF⟘AC ಆದರೆ ∆ABD ~ ∆ECF ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

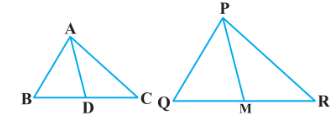
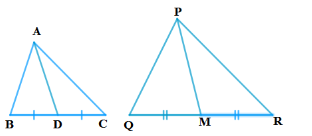
12. ಚಿತ್ರ 2.41 ರಲ್ಲಿ ∆ABC ಯ ಬಾಹುಗಳಾದ AB ಮತ್ತು BC ಹಾಗೂ ಮಧ್ಯರೇಖೆ AD ಗಳು ಕ್ರಮವಾಗಿ ∆PQRನ ಬಾಹುಗಳಾದ PQ ಮತ್ತು QR ಹಾಗೂ ಮಧ್ಯರೇಖೆ PM ನೊಂದಿಗೆ ಸಮಾನುಪಾತದಲ್ಲಿದ್ದರೆ ∆ABC ~ ∆PQR ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
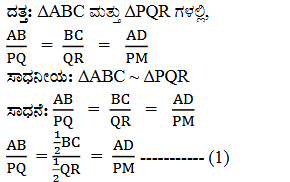

13. ∆ABC 3 ∠ADC = ∠BAC D ಯು BC ಆಗುವಂತೆ D ಯು BC ಬಾಹುವಿನ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. ಆದರೆ CA2 =CB. CD ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

14. ∆ABC ಯು ಬಾಹುಗಳಾದ AB ಮತ್ತು AC ಗಳು ಹಾಗೂ ಮಧ್ಯರೇಖೆ AD ಯು ಕ್ರಮವಾಗಿ ∆PQRನ ಬಾಹುಗಳಾದ PQ ಮತ್ತು PR ಹಾಗೂ ಮಧ್ಯರೇಖೆ PM ನೊಂದಿಗೆ ಸಮಾನುಪಾತ ಹೊಂದಿದ್ದರೆ ∆ABC ~ ∆PQR ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:



15. 6m ಎತ್ತರದ ನೇರವಾದ ಕಂಬವು ನೆಲದ ಮೇಲೆ 4m ಉದ್ದದ ನೆರಳನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ. ಅದೇ ಸಮಯದಲ್ಲಿ ಒಂದು ಕಟ್ಟಡವು 28 ಮೀಟರ್ ಉದ್ದದ ನೆರಳನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ ಹಾಗಾದರೆ ಆ ಕಟ್ಟಡದ ಎತ್ತರವೇನು?
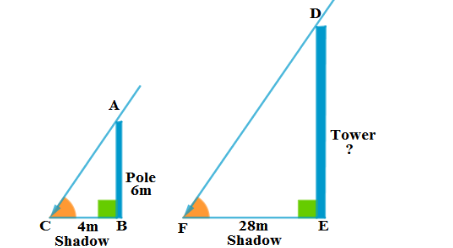
ಉತ್ತರ:

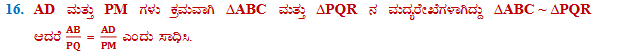
ಉತ್ತರ:

ಅಭ್ಯಾಸ 2.4
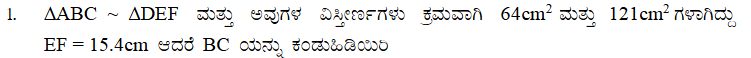
ಉತ್ತರ:

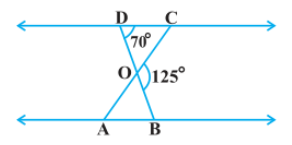
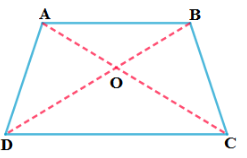
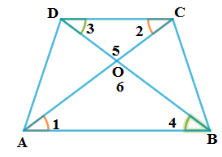
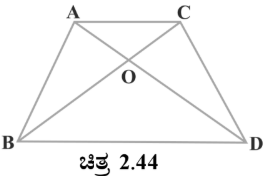
2. ∆BCD ತ್ರಾಪಿಜ್ಯದಲ್ಲಿ ABǁCD ಕರ್ಣಗಳು ಪರಸ್ಪರ O ಬಿಂದುವಿನ್ಲಿ ಛೇದಿಸುತ್ತದೆ. AB = 2CD ಆದರೆ ∆AOB ಮತ್ತು ∆COD ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

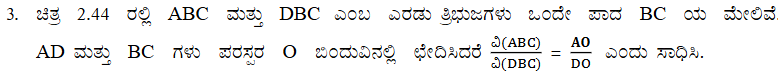
ಉತ್ತರ:
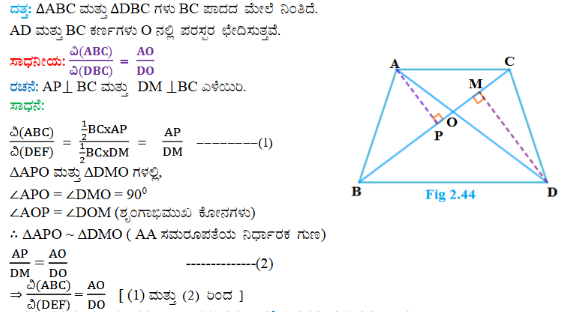
4. ಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳು ಸಮವಾದರೆ ಅವುಗಳು ಸರ್ವಸಮ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
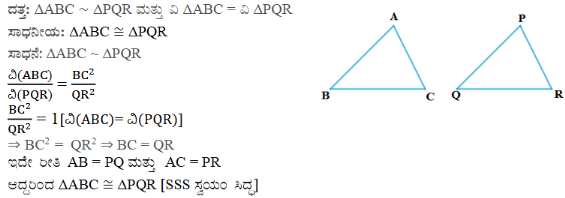
5. D. E ಮತ್ತು F ಗಳು ಕ್ರಮವಾಗಿ ∆ABC ಯ ಬಾಹುಗಳಾದ AB, BC ಮತ್ತು AC ಗಳ ಮಧ್ಯಬಿಂದುಗಳಾದರೆ ∆DEF ಮತ್ತು ∆ABCಯ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
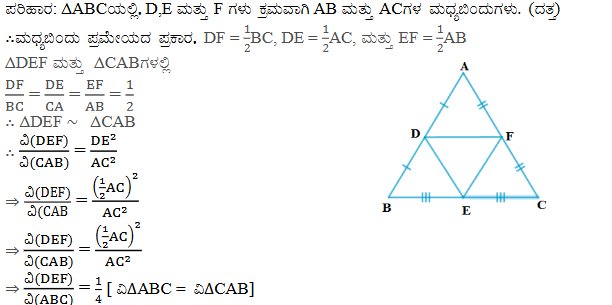
6. ಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತವು ಅವುಗಳ ಅನುರೂಪ ಮಧ್ಯರೇಖೆಗಳ ವರ್ಗಗಳ ಅನುಪಾತಕ್ಕೆ ಸಮ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
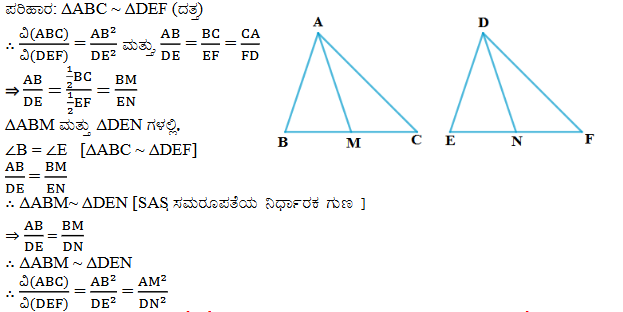
7. ವರ್ಗದ ಒಂದು ಬಾಹುವಿನ ಮೇಲೆ ರಚಿಸಿರುವ ಸಮಬಾಹು ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವು ಅದೇ ವರ್ಗದ ಒಂದು ಕರ್ಣದ ಮೇಲೆ ರಚಿಸಿರುವ ಸಮಬಾಹು ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣದ ಅರ್ಧದಷ್ಟು ಇರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
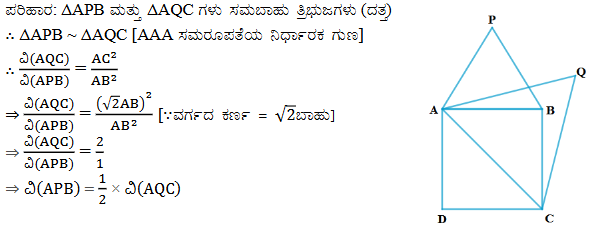
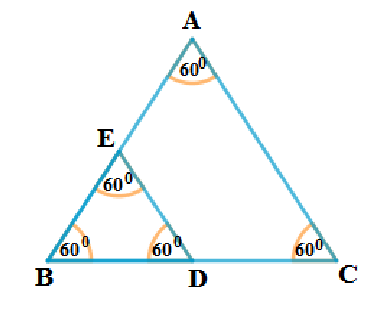
8. ∆ABC ಮತ್ತು ∆BDE ಗಳು ಎರಡು ಸಮಬಾಹು ತ್ರಿಭುಜಗಳು D ಯು BC ಯ ಮಧ್ಯಬಿಂದು ಆದರೆ ∆ABC ಮತ್ತು ∆BDE ಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತ
(A) 2:1 (B) 1:2
(C) 4:1 (D) 1:4
ಉತ್ತರ:

9. ಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ಬಾಹುಗಳ ಅನುಪಾತ 4:9 ಆದರೆ ಅವುಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತ
(A) 2:3 (B) 4:9
(C) 81: 16 (D) 16: 81
ಉತ್ತರ:

ಅಭ್ಯಾಸ 2.5
1. ತ್ರಿಭುಜಗಳ ಬಾಹುಗಳ ಅಳತೆಗಳನ್ನು ಕೆಳಗೆ ಕೊಡಲಾಗಿದೆ. ಅವುಗಳಲ್ಲಿ ಯಾವುದು ಲಂಬಕೋನ ತ್ರಿಭುಜವಾಗಿದೆ ಎಂದು ನಿರ್ಧರಿಸಿ. ಲಂಬಕೋನ ತ್ರಿಭುಜವಾದಲ್ಲಿ ವಿಕರ್ಣದ ಅಳತೆ ಬರೆಯಿರಿ.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
ಉತ್ತರ:
(i) ತ್ರಿಭುಜದ ಬಾಹುಗಳು ಕ್ರಮವಾಗಿ 7cm, 24cm ಮತ್ತು 25cm ಗಳು.
ಬಾಹುಗಳನ್ನು ವರ್ಗಗೊಳಿಸಿದಾಗ 49, 576 ಮತ್ತು 625.
49 +576 = 625 ಅಥವಾ 72+242 = 252
ಕೊಟ್ಟಿರುವ ತ್ರಿಭುಜದ ಬಾಹುಗಳು ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯವನ್ನು ಪ್ರತಿಪಾದಿಸುತ್ತವೆ.
ಆದ್ದರಿಂದ ಇದು ಲಂಬಕೋನ
ತ್ರಿಭುಜದ ವಿಕರ್ಣದ ಉದ್ದವು 25cm
(ii) ತ್ರಿಭುಜದ ಬಾಹುಗಳು ಕ್ರಮವಾಗಿ 3cm, 8cm ಮತ್ತು 6cm ಆಗಿರಲಿ ಬಾಹುಗಳನ್ನು ವರ್ಗಗೊಳಿಸಿದಾಗ,
9, 64 ಮತ್ತು 36 ಆಗುತ್ತದೆ
9 + 36 ≠ 64 ಅಥವಾ 32 +62 ≠ 82
ಆದ್ದರಿಂದ ಸ್ಪಷ್ಟವಾಗಿ ಎರಡು ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತವು ಮೂರನೇ ಬಾಹುವಿನ ವರ್ಗಕ್ಕೆ ಸಮನಾಗಿಲ್ಲ.
∴ ಕೊಟ್ಟಿರುವ ತ್ರಿಭುಜದ ಬಾಹುಗಳು ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯವನ್ನು ಪ್ರತಿಪಾದಿಸುವುದಿಲ್ಲ.
(iii) ತ್ರಿಭುಜದ ಬಾಹುಗಳು 50 cm, 80cm ಮತ್ತು 100cm
ಬಾಹುಗಳನ್ನು ವರ್ಗಗೊಳಿಸಿದಾಗ 2500, 6400 ಮತ್ತು 10000
ಹೇಗಾದರೂ 2500 + 6400 ≠ 10000 (ಅಥವಾ) 502 +802 ≠ 1002
ಆದ್ದರಿಂದ ಸ್ಪಷ್ಟವಾಗಿ ಎರಡು ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತವು ಮೂರನೇ ಬಾಹುವಿನ ವರ್ಗಕ್ಕೆ ಸಮನಾಗಿಲ್ಲವೆಂದು ತಿಳಿಯುತ್ತದೆ.
∴ ಕೊಟ್ಟಿರುವ ತ್ರಿಭುಜದ ಬಾಹುಗಳು ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯವನ್ನು ಪ್ರತಿಪಾದಿಸುವುದಿಲ್ಲ.
(iv) ಕೊಟ್ಟಿರುವ ಬಾಹುಗಳು13cm, 12cm, ಮತ್ತು 5cm
ಬಾಹುಗಳನ್ನು ವರ್ಗಗೊಳಿಸಿದಾಗ 169, 144 ಮತ್ತು 25cm
∴ ಇದನ್ನು 144 + 25 = 169 ಎಂದು ಬರೆಯಬಹುದು ಅಥವಾ 122 + 52 = 132
∴ ಕೊಟ್ಟಿರುವ ಬಾಹುಗಳು ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯವನ್ನು ಪ್ರತಿಪಾದಿಸುತ್ತವೆ.
∴ ಇದು ಲಂಬಕೋನ ತ್ರಿಭುಜ
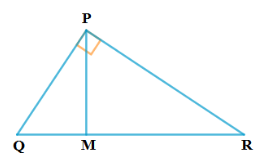
2. . ∆PQR ನಲ್ಲಿ P ಯು ಲಂಬಕೋನವಾಗಿದೆ. PM⟘QR ಆಗುವಂತೆ QR ಮೇಲೆ M ಒಂದು ಬಿಂದು. ಆದರೆ PM² = QM.MR ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

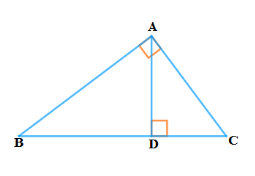
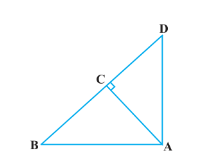
3. 2.53 ರಲ್ಲಿ ∆ABD A = 90° AC⟘BD ಆದರೆ
(i) AB² = BC. BD
(ii) AC² = BC. DC
(iii) AD² = BD. CD
ಉತ್ತರ:


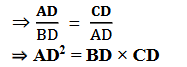
4. ABC ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜದಲ್ಲಿ C ಯು ಲಂಬಕೋನವಾಗಿದೆ AB² = 2AC2 ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
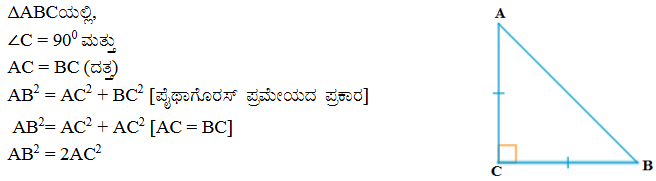
5. ABC ಯು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜದಲ್ಲಿ C ಯು ಲಂಬಕೋನವಾಗಿದೆ AB² = 2 AC2 ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
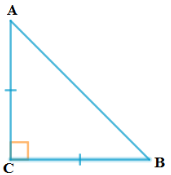
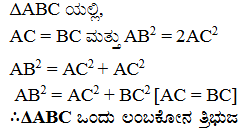
6. ABC ಯು ಬಾಹು 2a ಇರುವ ಸಮಬಾಹು ತ್ರಿಭುಜವಾಗಿದೆ ಅದರ ಪ್ರತಿಯೊಂದು ಎತ್ತರ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
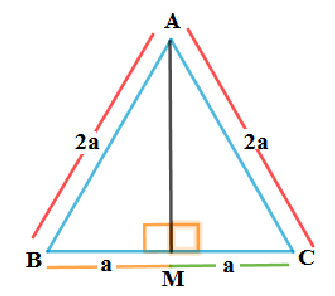

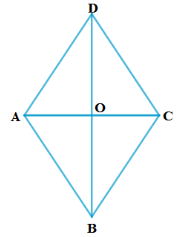
7. ಒಂದು ವಜ್ರಾಕೃತಿಯ ಎಲ್ಲಾ ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತವು ಅದರ ಕರ್ಣಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
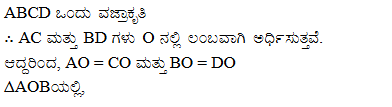
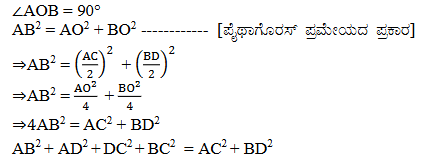
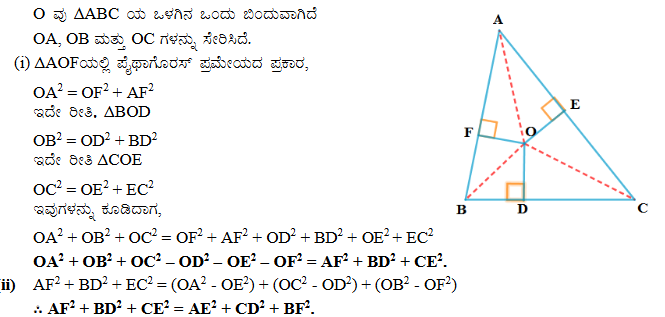
8. ಚಿತ್ರ 2.54 ರಲ್ಲಿ O ವು ABCಯ ಒಳಗಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ OD⟘BC, OE⟘AC and OF⟘AB ಆದರೆ
(i) OA² + OB² + OC² – OD² – OE² – OF2 = AF2 + BD² + CE²,
(ii) AF2 + BD² + CE² = AE2 + CD² + BF2.
ಉತ್ತರ:
9. 10m ಎತ್ತರವಿರುವ ಏಣಿಯು ನೆಲದಿಂದ 8m ಎತ್ತರದಲ್ಲಿ ಗೋಡೆಯಲ್ಲಿರುವ ಕಿಟಕಿಯನ್ನು ಮುಟ್ಟುತ್ತದೆ ಹಾಗಾದರೆ ಏಣಿಯ ಪಾದವು ನೆಲದಿಂದ ಎಷ್ಟು ದೂರದಲ್ಲಿದೆ?
ಉತ್ತರ:
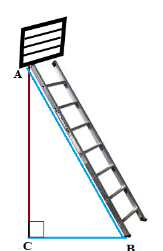

10. 24m ಉದ್ದದ ತಂತಿಯನ್ನು 18m ಎತ್ತರದ ಒಂದು ನೇರವಾದ ಕಂಬದ ತುದಿಗೆ ಕಟ್ಟಿ ಅದರ ಇನ್ನೊಂದು ತುದಿಯನ್ನು ನೆಲದ ಮೇಲಿರುವ ಗೂಟಕ್ಕೆ ಸೇರಿಸಲಾಗಿದೆ. ತಂತಿಯು ಬಿಗಿಯಾಗಿ ಇರುವಂತೆ ಕಟ್ಟಬೇಕಾದರೆ ಕಂಬದ ಬುಡದಿಂದ ಗೂಟವನ್ನು ಎಷ್ಟು ದೂರದವರೆಗೆ ಕೊಂಡೊಯ್ಯಬೇಕು?
ಉತ್ತರ:

11. ವಿಮಾನವೊಂದು ಒಂದು ನಿಲ್ದಾಣದಿಂದ ಹೊರಟು ಗಂಟೆಗೆ 1000km ಜವದಿಂದ ಉತ್ತರದ ಕಡೆಗೆ ಚಲಿಸುತ್ತದೆ. ಆದೇ ಸಮಯದಲ್ಲಿ ಮತ್ತೊಂದು ವಿಮಾನವು ಅದೇ ನಿಲ್ದಾಣದಿಂದ ಹೊರಟು ಗಂಟೆಗೆ 1200km ಜವದಿಂದ ಪಶ್ಚಿಮದ ಕಡೆಗೆ ಚಲಿಸುತ್ತದೆ. 1 1/2 ಗಂಟೆಗಳ ನಂತರ ವಿಮಾನಗಳ ನಡುವಿನ ಅಂತರ ಎಷ್ಟು?
ಉತ್ತರ:

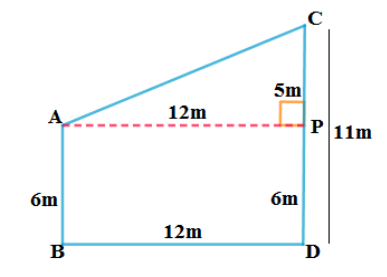
12. 6m ಮತ್ತು 11m ಉದ್ದದ ಎರಡು ಕಂಬಗಳು ಸಮತಟ್ಟಾದ ನೆಲದ ಮೇಲೆ ನಿಂತಿವೆ. ಆ ಕಂಬಗಳ ಪಾದಗಳ ನಡುವಿನ ಅಂತರ 12m ಆದರೆ ಅವುಗಳ ತುದಿಗಳ ನಡುವಿನ ಅಂತರವೇನು?
ಉತ್ತರ:

13. ∆ABC ಯಲ್ಲಿ ∠C = 900 D ಮತ್ತು E ಗಳು ಕ್ರಮವಾಗಿ CA ಮತ್ತು CB ಗಳ ಮೇಲಿನ ಬಿಂದುಗಳು ಆದರೆ AE2 + BD2 = AB2 + DE2 ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
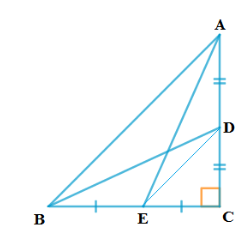
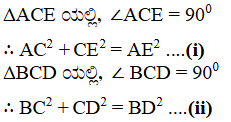

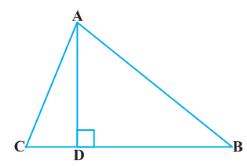
14. DB = 3 CD ಆಗುವಂತೆ ∆ABCಯಲ್ಲಿ A ನಿಂದ BC ಗೆ ಎಳೆದ ಲಂಬವು BCಯನ್ನು D ನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ (ಚಿತ್ರ 2.55ನ್ನು ನೋಡಿ) 2AB2 = 2AC2 + BC2 ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

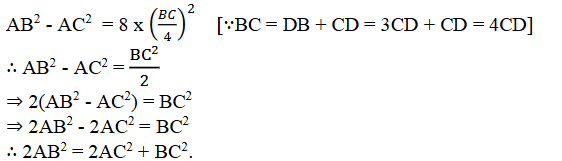
15. BD = 1/3 BC ಆಗುವಂತೆ ABC ಯಲ್ಲಿ ಸಮಬಾಹು D ಯು BCಯ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಾಗಿದೆ. 9AD2 = 7AB2 ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
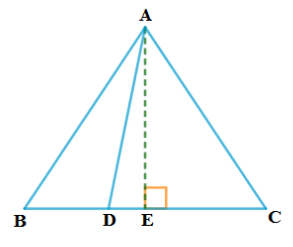
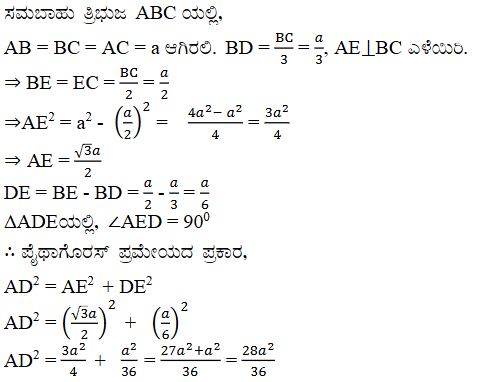
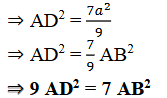
16. ಒಂದು ಸಮಬಾಹು ತ್ರಿಭುಜದಲ್ಲಿ ಒಂದು ಬಾಹುವಿನ ವರ್ಗದ ಮೂರರಷ್ಟು ಅದರ ಯಾವುದಾದರೊಂದು ಎತ್ತರದ ನಾಲ್ಕರಷ್ಟಕ್ಕೆ ಸಮ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
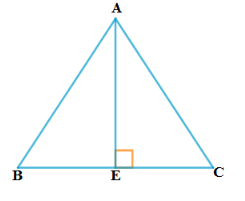
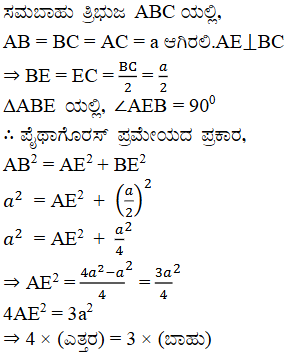
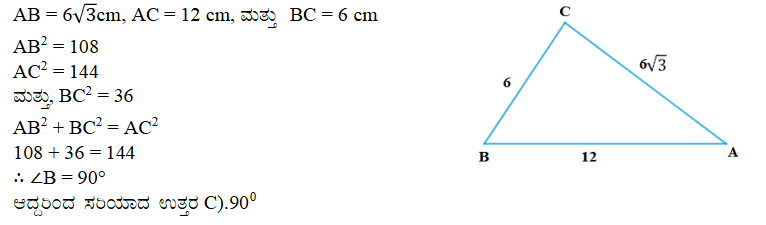
17. ಸರಿಯಾದ ಉತ್ತರ ಗುರ್ತಿಸಿ ಮತ್ತು ಸಮರ್ಥಿಸಿ. ∆ABC & AB = 6√3 cm, AC = 12cm ಮತ್ತು BC = 6cm ಆದರೆ B ಯು
(A) 120° (B) 60° (C) 90° (D) 45°
ಉತ್ತರ:
ಅಭ್ಯಾಸ 2.6 (ಐಚ್ಚಿಕ)
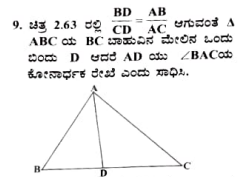
1. ಚಿತ್ರ 2.56 ರ ∆PQR ನಲ್ಲಿ PS ಇದು <QPR ನ ಕೋನಾರ್ಧಕ ರೇಖೆಯಾಗಿದೆ (QS)/(SR) = (PQ)/(PR) ಎಂದು ಸಾಧಿಸಿ.
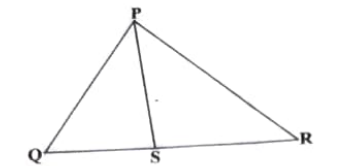
ಉತ್ತರ:

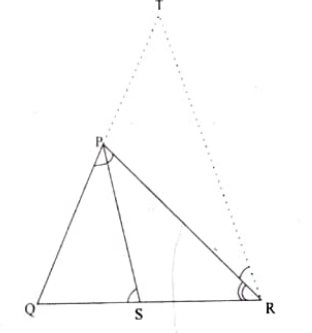


2. ಚಿತ್ರ 2.57 ರಲ್ಲಿ ∆ABC ಯ AC ವಿಕರ್ಣದ ಮೇಲೆ ಆ ಒಂದು ಬಿಂದುವಾಗಿದೆ BD⟘AC, DM⟘BC ಮತ್ತು DN⟘AB ಆದರೆ
(i) DM² = DN. MC
(ii) DN² = DM. AN ಎಂದು ಸಾಧಿಸಿ
ಉತ್ತರ:
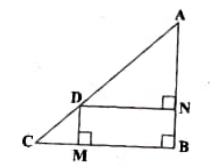



3. ಚಿತ್ರ 2.58 ರಲ್ಲಿ ∆ABC ಯಲ್ಲಿ ∠ABC = 90° ಮತ್ತು AD⟘CB ವೃದ್ಧಿಸಿದ ಭಾಗಕ್ಕೆ AC2 = AB2 + BC2 + 2 BC. BD ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

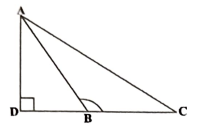
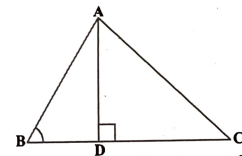
4. ಚಿತ್ರ 2.59 ರಲ್ಲಿ ∆ABC ∠ABC = 900 ಮತ್ತು AD⟘BC ಆದರೆ AC2 = AB2 + BC2 – 2BC.BD ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

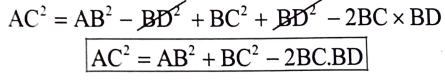
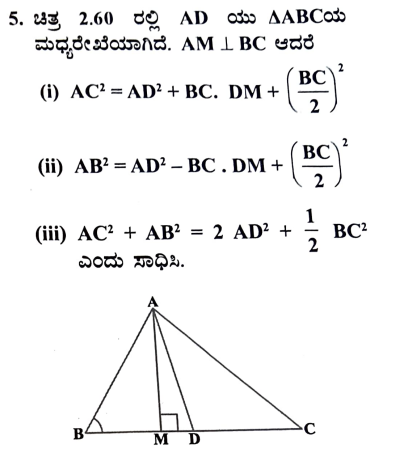
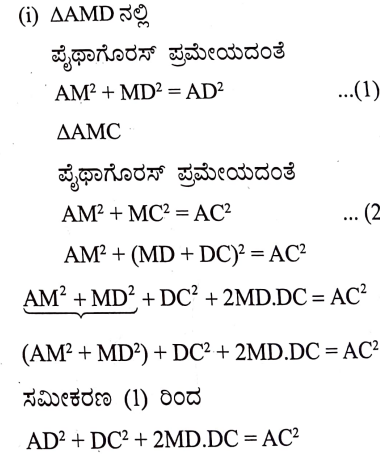
ಉತ್ತರ:
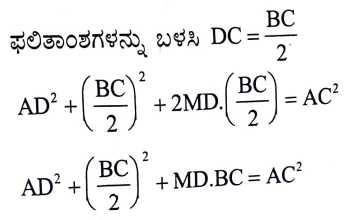


6. ಸಮಾಂತರ ಚತುರ್ಭುಜದ ಕರ್ಣಗಳ ವರ್ಗಗಳ ಮೊತವು ಅದರ ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮ ಎಂದು ಸಾಧಿಸಿ
ಉತ್ತರ:
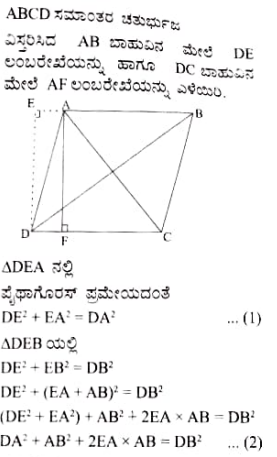


7. ಚಿತ್ರ 2.61 ರಲ್ಲಿ AB ಮತ್ತು CD ಜ್ಯಾಗಳು P ಬಿಂದುವಿನಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ. ಆದರೆ
(i) ΔAPC ~ ΔDPB
(ii) AP. PB = CP. DP ಎಂದು ಸಾಧಿಸಿ.
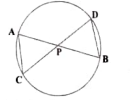
ಉತ್ತರ:
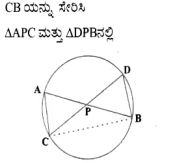

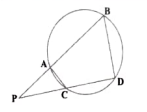
8. ಚಿತ್ರ 2.62 ರಲ್ಲಿ ಒಂದು ವೃತ್ತದ AB ಮತ್ತು CD ಜ್ಯಾಗಳು ವೃತ್ತದ ಹೊರಭಾಗದ Pಬಿಂದುವಿನಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ (ವೃದ್ಧಿಸಿದಾಗ) ಆದರೆ
(1) ΔРАС ~ ΔPDB
(ii) PA. PB = PC. PD ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

ಉತ್ತರ:
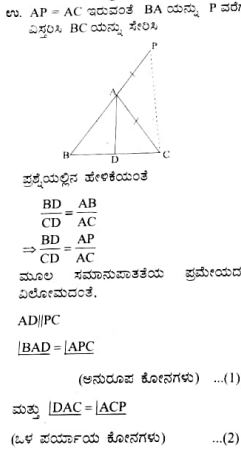

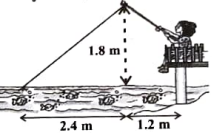
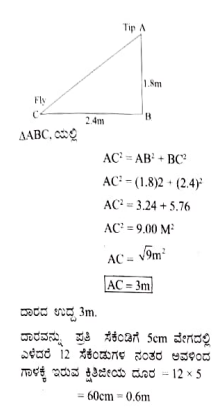
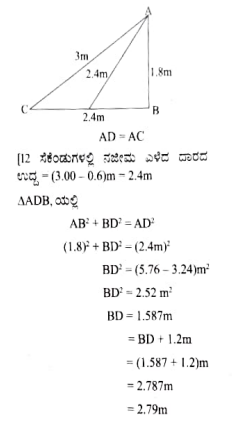
10. ನಜೀಮ ಒಂದು ಚಿಕ್ಕ ನದಿಯಲ್ಲಿ ಗಾಳ ಹಾಕಿ ಹಿಡಿಯುತ್ತಿರುತ್ತಾಳೆ. ಗಾಳದ ಸಲಾಕೆಯ ತುದಿಯು ನೀರಿನ ಮಟ್ಟದಿಂದ 1.8m ಎತ್ತರದಲ್ಲಿ ಮತ್ತು ದಾರದ ತುದಿಯಲ್ಲಿರುವ ಗಾಳವು ಅವಳಿಂದ ನೀರಿನ ಮೇಲ್ಮೈ ಮೇಲೆ 3.60 ದೂರದಲ್ಲಿದೆ ಹಾಗೂ ಗಾಳದ ಸಲಾಕೆಯ ತುದಿಗೆ ಲಂಬವಾಗಿರುವ ನೀರಿನ ಮೇಲ್ಮೈ ಬಿಂದುವಿನಿಂದ 2.4 ದೂರದಲ್ಲಿದೆ. ಗಾಳದ ದಾರವು (ಸಲಾಕೆಯ ತುದಿಯಿಂದ ಗಾಳದವರೆಗೆ) ಬಿಗಿಯಾಗಿದೆ ಎಂದು ಭಾವಿಸಿದಾಗ ಅವಳು ಎಷ್ಟು ಉದ್ದದ ದಾರ ಹೊರ ಹಾಕಬೇಕು? (ಚಿತ್ರ 2.64ನ್ನು ನೋಡಿ) ಅವಳು ದಾರವನ್ನು ಪ್ರತಿ ಸೆಕೆಂಡಿಗೆ 5cm ವೇಗದಲ್ಲಿ ಎಳೆದರೆ 12 ಸೆಕೆಂಡುಗಳ ನಂತರ ಅವಳಿಂದ ಗಾಳಕ್ಕೆ ಇರುವ ಕ್ಷಿತಿಜೀಯ ದೂರವೇನು?
ಉತ್ತರ:
AB ಗಾಳದ ಸಲಾಕೆಯ ಎತ್ತರ BC ಗಾಳದ ಸಲಾಕೆಯ ತುದಿಗೆ ಲಂಬವಾಗಿರುವ ನೀರಿನ ಮೇಲ್ಮೈ.
AC ದಾರದ ಉದ್ದ
ದಾರದ ಉದ್ದ AC ಯನ್ನು ಪೈಥಾಗೊರಸ್ ಪ್ರಮೇಯ ಬಳಸಿ ಕಂಡು ಹಿಡಿಯಬಹುದು.
ನೆನಪಿನಲ್ಲಿಡಬೇಕಾದ ಅಂಶಗಳು
1. ಎರಡು ತ್ರಿಭುಜಗಳು ಸಮರೂಪವಾಗಬೇಕಾದರೆ:
(1) ಅವುಗಳ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾಗಿರಬೇಕು ಮತ್ತು
(ii) ಅವುಗಳ ಅನುರೂಪ ಬಾಹುಗಳ ಅನುಪಾತ ಸಮ (ಸಮಾನುಪಾತ) ವಾಗಿರಬೇಕು.
2. ಎರಡು ತ್ರಿಭುಜಗಳಲ್ಲಿ ಒಂದು ತ್ರಿಭುಜದ ಮೂರು ಬಾಹುಗಳು ಮತ್ತೊಂದು ತ್ರಿಭುಜದ ಮೂರು ಬಾಹುಗಳೊಡನೆ ಸಮಾನುಪಾತ ಹೊಂದಿದ್ದರೆ (ಅಂದರೆ ಅನುಪಾತ ಒಂದೇ ಆದರೆ) ಅವುಗಳ ಅನುರೂಪ ಕೋನಗಳು ಸಮನಾಗಿರುತ್ತವೆ ಮತ್ತು ಅದ್ದರಿಂದಾಗಿ ಆ ಎರಡು ತ್ರಿಭುಜಗಳು ಸಮರೂಪಿಗಳಾಗಿರುತ್ತವೆ. ಈ ನಿರ್ಧಾರಕ ಗುಣವನ್ನು ಎರಡು ತ್ರಿಭುಜಗಳ ಸಮರೂಪತೆಯ ಬಾಹು-ಬಾಹು-ಬಾಹು (S.S.S) ನಿರ್ಧಾರಕ ಗುಣ ಎಂದು ಹೇಳಲಾಗಿದೆ.
ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣ = 1/2 x ಪಾದ x ಎತ್ತರ
3. ಎರಡು ತ್ರಿಭುಜಗಳಲ್ಲಿ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾದರೆ ಅವುಗಳ ಅನುರೂಪ ಬಾಹುಗಳ ಅನುಪಾತಗಳು ಸಮ (ಅಥವಾ ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ) ಆದ್ದರಿಂದ ಆ ತ್ರಿಭುಜಗಳು ಸಮರೂಪವಾಗಿರುತ್ತವೆ. ಈ ನಿರ್ಧಾರಕ ಗುಣವನ್ನು ಸರ್ವಸಮ ತ್ರಿಭುಜಗಳ ಕೋನ – ಕೋನ – ಕೋನ (ಕೋ. ಕೋ. ಕೋ) ನಿರ್ಧಾರಕ ಗುಣ ಎಂದು ಹೇಳಲಾಗಿದೆ. (ಅಥವಾ AAA ನಿರ್ಧಾರಕ ಗುಣ)
4. ತ್ರಿಭುಜದ ಯಾವುದಾದರೂ ಎರಡು ಬಾಹುಗಳನ್ನು ಸಮಾನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುವ ರೇಖೆಯು ಅದರ ಮೂರನೇ ಬಾಹುವಿಗೆ ಸಮಾನಾಂತರವಾಗಿರುತ್ತದೆ.
5. ಸಂಕೇತ ‘~’ ಸಮರೂಪ ಎಂಬುದನ್ನು ಸೂಚಿಸುತ್ತದೆ.
6. ಮೂಲ ಸಮಾನುಪಾತತೆಯ ಪ್ರಮೇಯ (ಫೇಲ್ಸ್ ಪ್ರಮೇಯ) : ತ್ರಿಭುಜದ ಎರಡು ಬಾಹುಗಳನ್ನು ಎರಡು ವಿಭಿನ್ನ ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವಂತೆ ಒಂದು ಬಾಹುವಿಗೆ ಸಮಾನಾಂತರವಾಗಿ ಎಳೆದ ಸರಳರೇಖೆಯು ಉಳಿದೆರಡು ಬಾಹುಗಳನ್ನು ಸಮಾನುಪಾತದಲ್ಲಿ ವಿಭಾಗಿಸುತ್ತದೆ.
7. ತ್ರಿಭುಜದ ಒಂದು ಕೋನವು ಮತ್ತೊಂದು ತ್ರಿಭುಜದ ಒಂದು ಕೋನಕ್ಕೆ ಸಮನಾಗಿದ್ದು ಆ ಕೋನಗಳನ್ನು ಉಂಟು ಮಾಡಿರುವ ಬಾಹುಗಳು ಸಮಾನುಪಾತದಲ್ಲಿದ್ದರೆ, ಆ ಎರಡು ತ್ರಿಭುಜಗಳು ಸಮರೂಪಿಗಳಾಗಿರುತ್ತವೆ. ಎರಡು ತ್ರಿಭುಜಗಳ ಸಮರೂಪತೆಯ ಈ ನಿರ್ಧಾರಕ ಗುಣಕ್ಕೆ ಬಾ.ಕೋ.ಬಾ (S.A.S) ನಿರ್ಧಾರಕ ಗುಣ ಎಂದು ಉಲ್ಲೇಖಿಸಲಾಗಿದೆ.
8. ಒಂದು ತ್ರಿಭುಜದಲ್ಲಿ ಅತ್ಯಂತ ದೊಡ್ಡ ಬಾಹುವಿನ ಮೇಲಿನ ವರ್ಗವು ಉಳಿದೆರಡು ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮನಾದರೆ ಆ ಎರಡು ಬಾಹುಗಳ ನಡುವೆ ಲಂಬಕೋನ ಏರ್ಪಡುತ್ತದೆ.
9. ಎರಡು ಸಮರೂಪ ತ್ರಿಭುಜಗಳ ವಿಸ್ತೀರ್ಣಗಳ ಅನುಪಾತವು ಅವುಗಳ ಅನುರೂಪ ಬಾಹುಗಳ ವರ್ಗಗಳ ಅನುಪಾತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
10. ಬಾಹುಗಳ ಸಂಖ್ಯೆ ಒಂದೇ ಇರುವ ಎರಡು ಬಹುಭುಜಾಕೃತಿಗಳು ಸಮರೂಪಿಗಳಾಗಬೇಕಾದರೆ (i) ಅವುಗಳ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾಗಿರಬೇಕು ಮತ್ತು (ii) ಅವುಗಳ ಅನುರೂಪ ಬಾಹುಗಳ ಅನುಪಾತ ಸಮವಾಗಿರಬೇಕು. (ಅಥವಾ ಸಮಾನುಪಾತದಲ್ಲಿರಬೇಕು)
11. ಒಂದು ಲಂಬಕೋನ ತ್ರಿಭುಜದಲ್ಲಿ ವಿಕರ್ಣದ ಮೇಲಿನ ವರ್ಗವು ಉಳಿದೆರಡು ಬಾಹುಗಳ ವರ್ಗಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
ಇತರೆ ವಿಷಯಗಳು :
ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು ನೋಟ್ಸ್
10ನೇ ತರಗತಿ ಗಣಿತ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳು ನೋಟ್ಸ್
