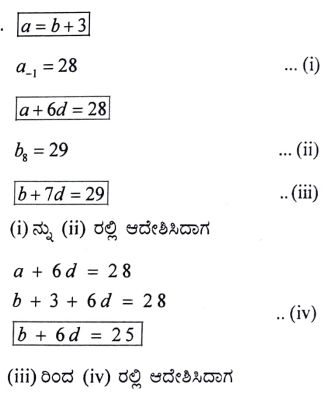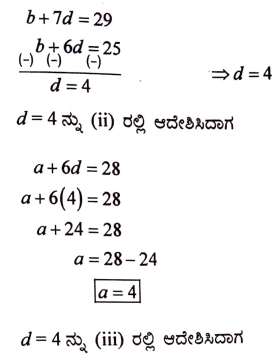10ನೇ ತರಗತಿ ಗಣಿತ ಪೂರಕ ಪರೀಕ್ಷಾ ಪ್ರಶ್ನೆಪತ್ರಿಕೆ ಜೂನ್ – 2020, SSLC Supplementary Exam Question Paper 2020 (ಉತ್ತರಸಹಿತ) 10ನೇ ತರಗತಿ ಗಣಿತ ಮಾದರಿ ಪ್ರಶ್ನೆ ಪತ್ರಿಕೆಗಳು 2020 pdf 10th standard maths exam question paper with solution sslc 2020 maths question paper with answer sslc question paper 2020 karnataka pdf with answers maths maths board paper 2020 class 10 solutions pdf download 2020 maths question paper solved karnataka sslc question papers with answers pdf maths

SSLC Supplementary Exam Question Paper 2020
I. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಅಥವಾ ಅಪೂರ್ಣ ಹೇಳಿಕೆಗಳಿಗೆ ನಾಲ್ಕು ಪರ್ಯಾಯ ಉತ್ತರಗಳನ್ನು ನೀಡಲಾಗಿದೆ. ಅವುಗಳಲ್ಲಿ ಸರಿಯಾದ ಉತ್ತರವನ್ನು ಆರಿಸಿ. ಕ್ರಮಾಕ್ಷರದೊಡನೆ ಪೂರ್ಣ ಉತ್ತರವನ್ನು ಬರೆಯಿರಿ. 8 x 1 = 8
1. ಕೊಟ್ಟಿರುವ ನಕ್ಷೆಯಲ್ಲಿ y = p(x) ಬಹುಪದೋಕ್ತಿಯ ಶೂನ್ಯತೆಗಳ ಸಂಖ್ಯೆಯು
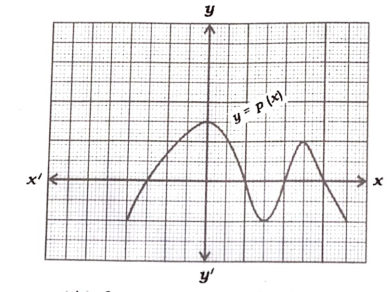
(A) 3 (B) 5 (C) 4 (D) 2
ಉತ್ತರ:
(C) 4
2. sec2 260 – tan2 260

ಉತ್ತರ:
(D) 1
3. ತ್ರಿಭುಜ ABC ಯಲ್ಲಿ DE || AC ಆಗಿದ್ದು, ಇವುಗಳಲ್ಲಿ ಸರಿಯಾದ ಸಂಬಂಧವು
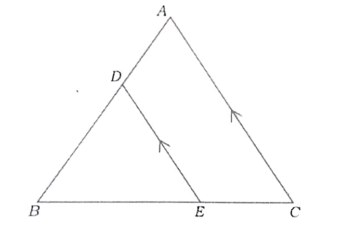
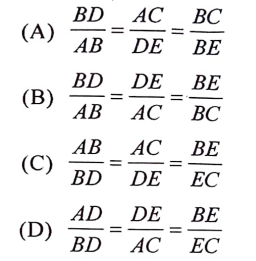
ಉತ್ತರ:
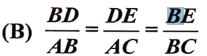
4. ಒಂದು ನೇರ ವೃತ್ತಪಾದ ಸಿಲಿಂಡರ್ ಹಾಗೂ ನೇರ ವೃತ್ತಪಾದ ಶಂಕುವಿನ ಪಾದ ಮತ್ತು ಎತ್ತರಗಳು ಸಮನಾಗಿದ್ದು, ಸಿಲಿಂಡರಿನ ಘನಫಲವು 360 cm3 ಆದರೆ ಶಂಕುವಿನ ಘನಫಲವು,
(A) 120 cm3 (B) 180cm3
(C) 90c m3 (D) 360cm3
ಉತ್ತರ:
(A) 120 cm3
5. x + 2y – 4 = 0 ಮತ್ತು 2x + 4y – 12 = 0 ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು,
(A) ಛೇಧಿಸುವ ರೇಖೆಗಳು
(B) ಸಮಾಂತರ ರೇಖೆಗಳು
(C) ಐಕ್ಯವಾಗುವ ರೇಖೆಗಳು
(D) ಪರಸ್ಪರ ಲಂಬರೇಖೆಗಳು
ಉತ್ತರ:
(B) ಸಮಾಂತರ ರೇಖೆಗಳು
6. ಒಂದು ಸಮಾಂತರ ಶ್ರೇಢಿಯ nನೇ ಪದ an= 3n – 2 ಆದಾಗ, ಆ ಶ್ರೇಢಿಯ 9 ನೇ ಪದವು
(A) -25 (B) 5
(C)-5 (D) 25
ಉತ್ತರ:
(D) 25
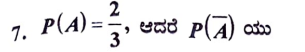

ಉತ್ತರ:
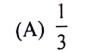
8. 7 ಸೆಂ.ಮೀ. ತ್ರಿಜ್ಯವಿರುವ ಗೋಳದ ಮೇಲೆ ವಿಸ್ತೀರ್ಣವು
(A) 154 ಚ.ಸೆಂ.ಮೀ (B) 616 ಚ.ಸೆಂ.ಮೀ
(C) 616 ಚ.ಸೆಂ.ಮೀ (D) 308 ಚ.ಸೆಂ.ಮೀ
ಉತ್ತರ:
(C) 616 ಚ.ಸೆಂ.ಮೀ
II. ಪ್ರತಿ ಉತ್ತರಕ್ಕೆ ಒಂದೊಂದು ಅಂಕದಂತೆ 8 x 1 = 8
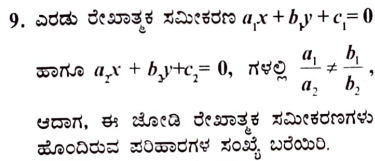
ಉತ್ತರ:
ನಿಖರವಾಗಿ ಒಂದು ಪರಿಹಾರ
ಪರ್ಯಾಯ ಉತ್ತರ
ಅನನ್ಯ ಪರಿಹಾರ
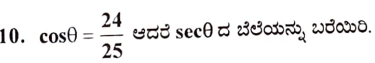
ಉತ್ತರ:
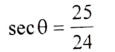
11. ಚಿತ್ರದಲ್ಲಿರುವಂತೆ ‘O’ ಕೇಂದ್ರವಿರುವ ವೃತ್ತದಲ್ಲಿ AC ಒಂದು ವ್ಯಾಸವಾಗಿದೆ. ∠ACB = 500 ಆದರೆ, ∠BAC ಯ ಅಳತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
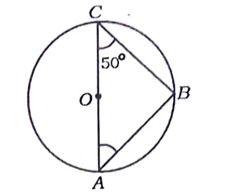
ಉತ್ತರ:
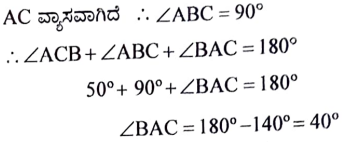
12. ವೃತ್ತಪಾದದ ತ್ರಿಜ್ಯ ‘r’ ಮತ್ತು ಓರೆ ಎತ್ತರ ‘lʼ ಆಗಿರುವ ಒಂದು ನೇರ ವೃತ್ತಪಾದ ಶಂಕುವಿನ ಪೂರ್ಣ ಮೇಲ್ಮೈ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯುವ ಸೂತ್ರವನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
ಶಂಕುವಿನ ಪೂರ್ಣ ಮೇಲೆ ವಿಸ್ತೀರ್ಣ
= πr(r + l)
13. ಅತೀ ಚಿಕ್ಕ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ ಹಾಗೂ ಅತೀ ಚಿಕ್ಕ ಸಂಯುಕ್ತ ಸಂಖ್ಯೆಗಳ ಮ.ಸಾ.ಅ. ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಅತೀ ಚಿಕ್ಕ ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆ = 2
ಅತೀ ಚಿಕ್ಕ ಸಂಯುಕ್ತ ಸಂಖ್ಯೆ = 4
ಆದ್ದರಿಂದ ಅವುಗಳ ಮ.ಸಾ.ಅ (2, 4) = 2
14. P(x) = 2x3 + 3x2 – 11x + 6 ಆದರೆ, P(1) ರ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
P(x) = 2x3 + 3x2 – 11x + 6
P(1) = 2(1)3 + 3(1)2 – 11(1) + 6
P(1) = 2 + 3 – 11 + 6
P(1) = 0
15. (x + 4)(x + 3) = 0 ಸಮೀಕರಣದಲ್ಲಿ ಒಂದು ಮೂಲವು – 4 ಆದರೆ, ಆ ಸಮೀಕರಣದ ಇನ್ನೊಂದು ಮೂಲವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
(x + 4)(x + 3) = 0
ಒಂದು ಮೂಲ – 4 ಆದರೆ, ಮತ್ತೊಂದು x + 3 = 0
x = – 3
16. sin2 A = 0 , ಆದಾಗ cosA ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
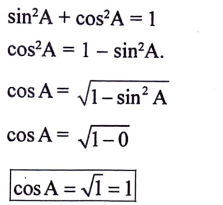
17. ಈ ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ಬಿಡಿಸಿ:
2x + 3y = 11
2x – 4y = – 24
ಉತ್ತರ:
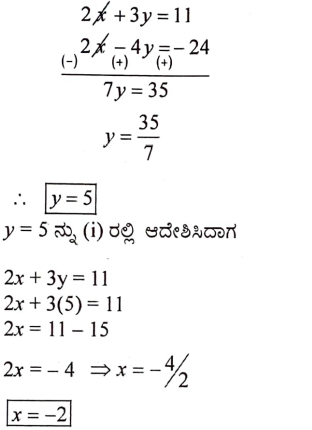
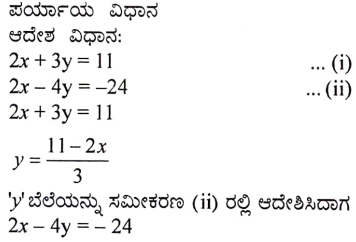
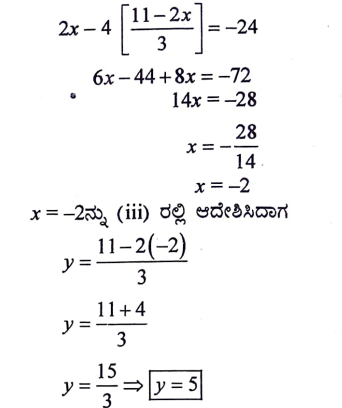
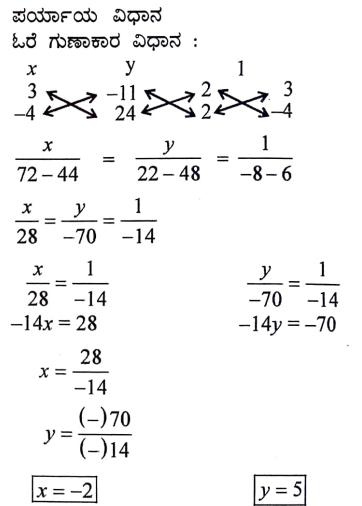
18. 5 + 10 + 15 +…. ಈ ಸಮಾಂತರ ಶ್ರೇಣಿಯ ಮೊದಲ 20 ಪದಗಳ ಮೊತ್ತವನ್ನು ಸೂಕ್ತವಾದ ಸೂತ್ರದ ಸಹಾಯದಿಂದ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
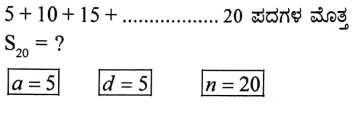
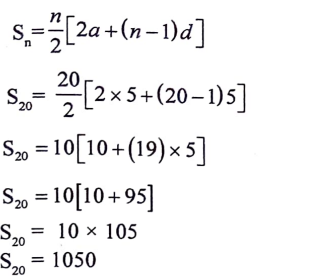
19. P(x) = 2x2 – 6x + k ಈ ಬಹುಪದೋಕ್ತಿಯ ಶೂನ್ಯತೆಗಳ ಮೊತ್ತವು ಅವುಗಳ ಗುಣಲಬ್ಧದ ಅರ್ಧದಷ್ಟಕ್ಕೆ ಸಮನಾದರೆ K ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

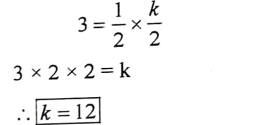
20. 2x2 – 5x -1=0 ವರ್ಗಸಮೀಕರಣದ ಶೋಧಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ ಮತ್ತು ಇದರಿಂದ ಮೂಲಗಳ ಸ್ವಭಾವವನ್ನು ನಿರ್ಧರಿಸಿ ಬರೆಯಿರಿ.
ಉತ್ತರ:
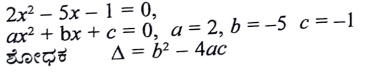

21. cosec A(1 – cosA)(cosec A + cotA) = 1 ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

ಅಥವಾ
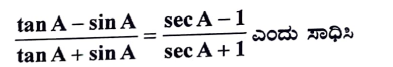
ಉತ್ತರ:
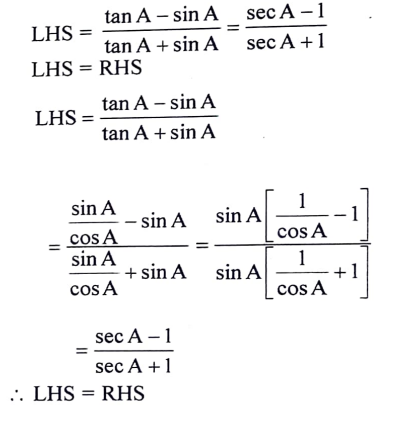
22. (2, 3) ಮತ್ತು (4, 7) ಬಿಂದುಗಳನ್ನು ಸೇರಿಸುವ ರೇಖಾಖಂಡದ ಮಧ್ಯಬಿಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
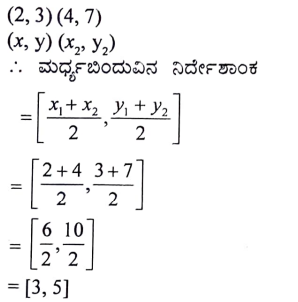
23. ಇಂಗ್ಲಿಷ್ ವರ್ಣಮಾಲೆಯ ಅಕ್ಷರಗಳಿಂದ A B C D E I ಗಳನ್ನು ಒಂದು ಘನಾಕೃತಿಯ ದಾಳದ ಮುಖಗಳ ಮೇಲೆ ಗುರುತಿಸಿದೆ. ಈ ದಾಳವನ್ನು ಒಂದು ಬಾರಿ ಉರುಳಿಸಿದಾಗ ಮೇಲೆ ಬರುವ ಮುಖದಲ್ಲಿ ಸ್ವರಾಕ್ಷರ (Vowel) ಬರುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
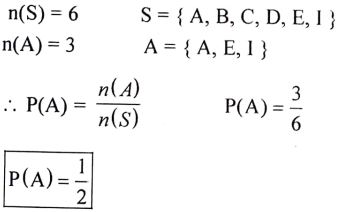
ಅಥವಾ
ಒಂದು ಅವಕಾಶದ ಆಟದಲ್ಲಿ ಒಂದು ಸೂಚಕವು ಚಿತ್ರಕಾರವಾಗಿ ತಿರುಗಿ 1, 2, 3, 4, 5, 6, 7, 8 ಅಂಕೆಗಳಲ್ಲಿ ಯಾವುದಾದರೊಂದು ಅಂಕೆಯನ್ನು ಸೂಚಿಸುವಂತೆ ನಿಶ್ಚಲವಾಗುತ್ತದೆ ಮತ್ತು ಇವೆಲ್ಲವೂ ಸಮಾನ ಸಾಧ್ಯತೆಗಳನ್ನು ಹೊಂದಿದೆ. ಸೂಚಕವು ಸೂಚಿಸುವ ಸಂಖ್ಯೆ ಒಂದು ಬೆಸ ಸಂಖ್ಯೆ ಆಗಿರುವ ಸಂಭವನೀಯತೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
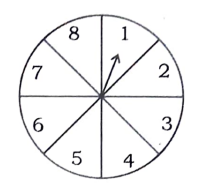
ಉತ್ತರ:

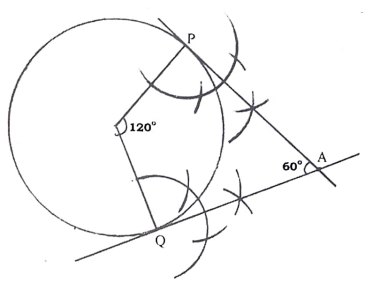
24. 4 ಸೆಂ.ಮೀ. ತ್ರಿಜ್ಯವುಳ್ಳ ವೃತ್ತವನ್ನು ರಚಿಸಿ, ಎರಡು ಸ್ಪರ್ಶಕಗಳ ನಡುವಿನ ಕೋನ 60° ಇರುವಂತೆ ವೃತ್ತಕ್ಕೆ ಒಂದು ಜೊತೆ ಸ್ಪರ್ಶಕಗಳನ್ನು ರಚಿಸಿ.
ಉತ್ತರ:
IV. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ. 3 x 9 = 27
25. √3ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

a ಮತ್ತು b ಎರಡು ಪೂರ್ಣಂಕ (b ≠ 0)
a ಮತ್ತು b ಗಳು 1 ನ್ನು ಹೊರತುಪಡಿಸಿ ಬೇರೆ ಸಾಮಾನ್ಯ ಅಪವರ್ತನವನ್ನು ಹೊಂದಿದ್ದರೆ, ಸಾಮಾನ್ಯ ಅಪವರ್ತನದಿಂದ ಭಾಗಿಸಬಹುದು.
∴ a ಮತ್ತು b ಗಳು ಸಹ ಅವಿಭಾಜ್ಯಗಳು
∴ b√(3) = a
ಎರಡೂ ಕಡೆ ವರ್ಗಗೊಳಿಸಿ ಮರುಜೋಡಿಸಿದಾಗ
3b2 = a2
∴ 3 ಇದು a2 ನ್ನು ಭಾಗಿಸುತ್ತದೆ.
∴ 3 ಇದು a ಯನ್ನು ಭಾಗಿಸುತ್ತದೆ
a = 3c ಎಂದು ಬರೆಯಬೇಕು
∴ (3c)2 = 3b2
9c2 = 3b2
3c2 = b2
b2 = 3c2
ಅಂದರೆ 3 ಇದು b2 ನ್ನು ಭಾಗಿಸುತ್ತದೆ.
3 ಇದು bನ್ನು ಭಾಗಿಸುತ್ತದೆ
∴ a ಮತ್ತು b ಗಳು ಕನಿಷ್ಠ 3ನ್ನು ಸಮಾನ್ಯ ಅಪವರ್ತನವಾಗಿ ಹೊಂದಿದೆ.
∴ a ಮತ್ತು b ಗಳು ಸಹ ಅವಿಭಾಜ್ಯಗಳು ಎಂಬ ಸತ್ಯಸಂಗತಿಗೆ ವಿರುದ್ಧವಾಗಿದೆ
∴ √(3) ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂಬ ನಮ್ಮ ಊಹೆ ತಪ್ಪು :
∴ √(3) ಒಂದು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ
ಸೂಚನೆ: ಪರ್ಯಾಯ ವಿಧಾನದಲ್ಲಿ ಸಾಧಿಸಿದರೆ ಅಂಕ ನೀಡಬಹುದು.
ಅಥವಾ
ಮತ್ತು 12 ಇವುಗಳ ಲ.ಸಾ.ಅ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
(306, 657) ರ ಮ.ಸಾ.ಅ
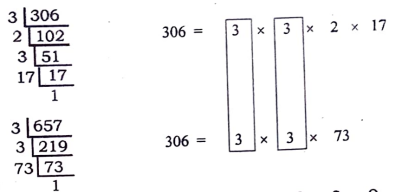
(306, 657) ರ ಮ.ಸಾ.ಅ = 3 x 3 = 9
ii) ಪರ್ಯಾಯ ವಿಧಾನ
(306, 657) ರ ಮ.ಸಾ.ಅ

∴ (306, 657) ರ ಮ.ಸಾ.ಅ = 9
iii) 9 ಮತ್ತು 12 ರ ಲ .ಸಾ.ಅ
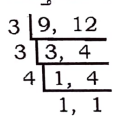
∴ 9 ಮತ್ತು 12 ರ ಲ .ಸಾ.ಅ = 3 x 3 x 4 = 36
∴ 9 ಮತ್ತು 12 ರ ಲ .ಸಾ.ಅ = 36
26. ಒಂದು ಆಯತಾಕಾರದ ಆಟದ ಮೈದಾನದ ಕರ್ಣವು ಅದರ ಚಿಕ್ಕ ಬಾಹುವಿಗಿಂತ 60 ಮೀ. ಹೆಚ್ಚಾಗಿದೆ ಮತ್ತು ಅದರ ದೊಡ್ಡ ಬಾಹುವು ಚಿಕ್ಕ ಬಾಹುವಿಗಿಂತ 30 ಮೀ ಹೆಚ್ಚಾಗಿದ್ದರೆ. ಆಟದ ಮೈದಾನದ ಬಾಹುಗಳ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
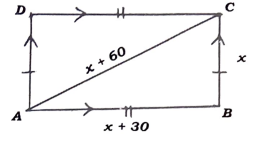

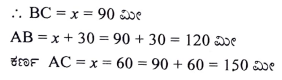
ಅಥವಾ
ಒಂದು ತ್ರಿಭುಜದ ಎತ್ತರವು ಅದರ ಪಾದಕ್ಕಿಂತ 6 ಸೆಂ.ಮೀ. ಹೆಚ್ಚಾಗಿದೆ. ತ್ರಿಭುಜದ ವಿಸ್ತೀರ್ಣವು 108 ಚ. ಸೆಂ.ಮೀ. ಆದಾಗ ತ್ರಿಭುಜದ ಪಾದ ಮತ್ತು ಎತ್ತರಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
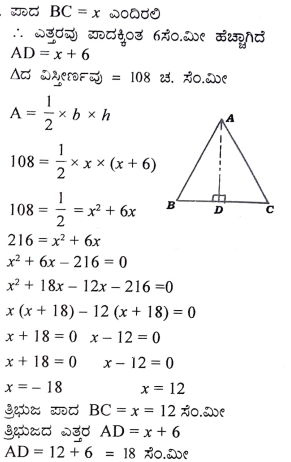
27. ಚಿತ್ರದಲ್ಲಿ △ABC ಯ ಶೃಂಗಗಳು A (0,6), B(8, 0) ಮತ್ತು C(5,8) ಆಗಿವೆ. CD ⊥ AB ಆದಾಗ ಆ ತ್ರಿಭುಜದ ಎತ್ತರ CD ಯ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
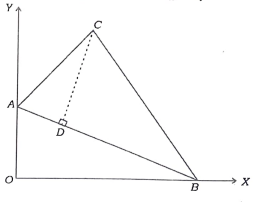
ಉತ್ತರ:
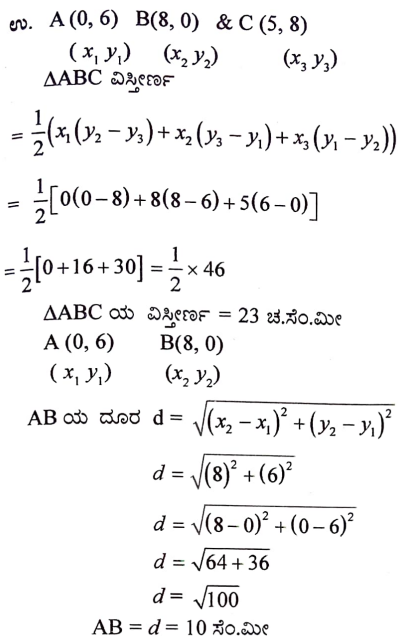

ಅಥವಾ
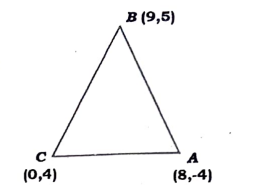
ಒಂದು ತ್ರಿಭುಜದ ಶೃಂಗಗಳು A (8,-4), B (9,5) ಮತ್ತು C (0,4) ಆಗಿದ್ದಾಗ ಅದು ಸಮದ್ವಿಬಾಹು ತ್ರಿಭುಜವಾಗಿರುತ್ತದೆ ಎಂದು ತೋರಿಸಿ.
ಉತ್ತರ:
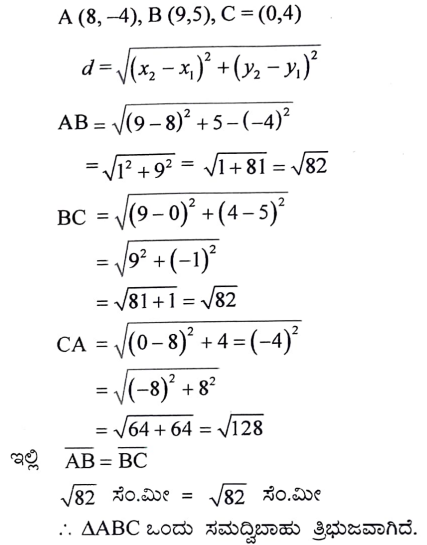
28. ಈ ಕೆಳಗಿನ ದತ್ತಾಂಶಗಳಿಗೆ ಮಧ್ಯಾಂಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ:
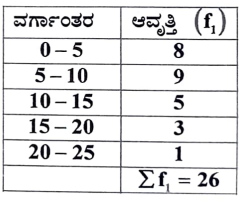
ಉತ್ತರ:
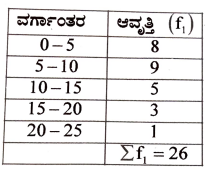
ಅತೀ ಹೆಚ್ಚು ಆವೃತ್ತಿ ಇರುವ ವರ್ಗಾಂತರ 5-10
ವರ್ಗಾಂತರ ಕೆಳಮಿತಿ 1 = 5
ವರ್ಗಾಂತರ ಆವೃತ್ತಿ f1 = 19
ಹಿಂದಿನ ವರ್ಗಾಂತರ ಆವೃತ್ತಿ f0 = 8
ಮುಂದಿನ ವರ್ಗಾಂತರ ಆವೃತ್ತಿ f2 = 5
ಗಾತ್ರ h = 5
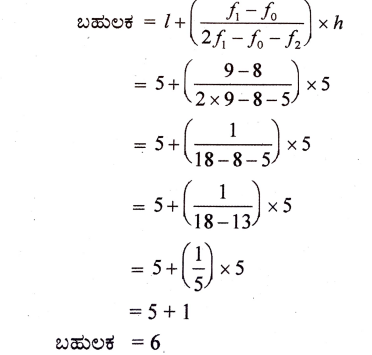
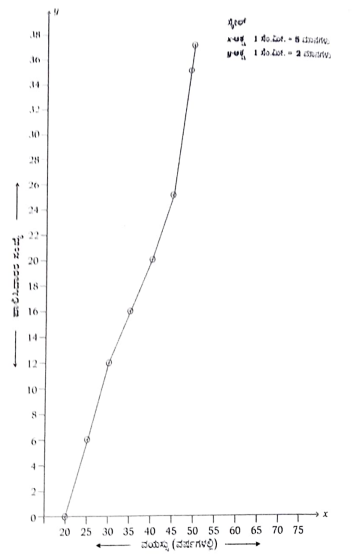
29. ಒಬ್ಬ ವಿಮಾ ಪಾಲಿಸಿ ಏಜೆಂಟನು ಪಡೆದ 35 ಪಾಲಿಸಿದಾರರ ವಯಸ್ಸುಗಳ ವಿತರಣೆಯ ದತ್ತಾಂಶಗಳು ಕೆಳಗಿನಂತೆ ಇವೆ. ಈ ದತ್ತಾಂಶಗಳಿಗೆ ‘ಕಡಿಮೆ ವಿಧಾನ’ದ ಓಜೀವ್ ರಚಿಸಿ:
ವಯಸ್ಸು (ವರ್ಷಗಳಲ್ಲಿ) ಪಾಲಿಸಿದಾರರ ಸಂಖ್ಯೆ
20 ಕ್ಕಿಂತ ಕಡಿಮೆ 2
25 ಕ್ಕಿಂತ ಕಡಿಮೆ 6
30 ಕ್ಕಿಂತ ಕಡಿಮೆ 12
35 ಕ್ಕಿಂತ ಕಡಿಮೆ 16
40 ಕ್ಕಿಂತ ಕಡಿಮೆ 20
45 ಕ್ಕಿಂತ ಕಡಿಮೆ 25
50 ಕ್ಕಿಂತ ಕಡಿಮೆ 35
ಉತ್ತರ:
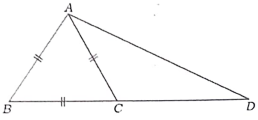
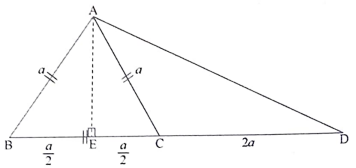
30. ΔABD, 60 BC: CD =1: 2 ಆಗುವಂತೆ BD ಯ ಮೇಲೆ Cಯು ಒಂದು ಬಿಂದು ಮತ್ತು ΔABC ಯು ಸಮಬಾಹು ತ್ರಿಭುಜವಾಗಿದ್ದರೆ AD2= 7AC² ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:

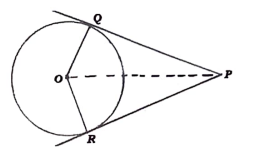
31. “ಬಾಹ್ಯ ಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳ ಉದ್ದವು ಸಮನಾಗಿರುತ್ತದೆ’ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
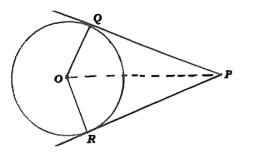


ಪರ್ಯಾಯ ವಿಧಾನ:

32. ತ್ರಿಜ್ಯಗಳು 21 ಸೆಂ.ಮೀ. ಮತ್ತು 7 ಸೆಂ.ಮೀ. ಆಗಿರುವ ‘O’ ಕೇಂದ್ರವುಳ್ಳ ಎರಡು ಏಕಕೇಂದ್ರಿಯ ವೃತ್ತಗಳ ಕಂಸಗಳು ಕ್ರಮವಾಗಿ AB ಮತ್ತು CD ಆಗಿವೆ. ಚಿತ್ರದಲ್ಲಿ ∠AOB = 300 ಆದಾಗ ಛಾಯೆಗೊಳಿಸಿದ ಭಾಗದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
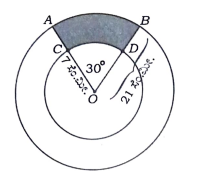
ಉತ್ತರ:

ಅಥವಾ
ABCD ಚೌಕದಲ್ಲಿ ಎರಡು ಅರ್ಧವೃತ್ತಗಳು ಒಂದನ್ನೊಂದು P ಬಿಂದುವಿನಲ್ಲಿ ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಿರುವಂತೆ ಬಾಹ್ಯವಾಗಿ ಸ್ಪರ್ಶಿಸಿವೆ. ಈ ಪ್ರತಿಯೊಂದು ಅರ್ಧವೃತ್ತದ ಕಂಸದ ಉದ್ದ 11 ಸೆಂ.ಮೀ.ಗೆ ಸಮನಾದಾಗ ಛಾಯೆಗೊಳಿಸಿದ ಭಾಗದ ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
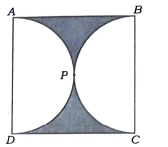
ಉತ್ತರ:

33. 6 ಸೆಂ.ಮೀ, 7 ಸೆಂ.ಮೀ ಮತ್ತು 8 ಸೆಂ.ಮೀ ಬಾಹುಗಳಿರುವ ಒಂದು ತ್ರಿಭುಜವನ್ನು ರಚಿಸಿ. ನಂತರ ಮತ್ತೊಂದು ತ್ರಿಭುಜವನ್ನು ಅದರ ಪ್ರತಿಯೊಂದು ಬಾಹುವು ಮೊದಲು ರಚಿಸಿದ ತ್ರಿಭುಜದ ಅನುರೂಪ ಬಾಹುಗಳ 3/7 ರಷ್ಟಿರುವಂತೆ ರಚಿಸಿ.
ಉತ್ತರ:
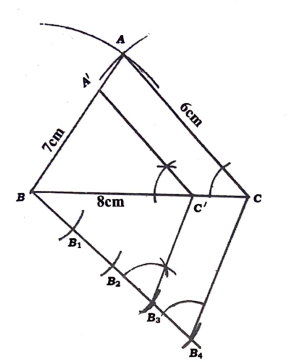
ತ್ರಿಭುಜದ ರಚನೆ ಲಘುಕೋನವನ್ನು ರಚಿಸಿ 4 ಭಾಗಗಳಾಗಿ ವಿಭಾಗಿಸುವುದು ಸಮಾಂತರ ರೇಖೆಗಳನ್ನು ಎಳೆಯುವುದು (2 ಜೊತೆ) A’ BC’ ತ್ರಿಭುಜದ ರಚನೆ
V. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗಳಿಗೆ ಉತ್ತರಿಸಿ. 4 x 4 = 16
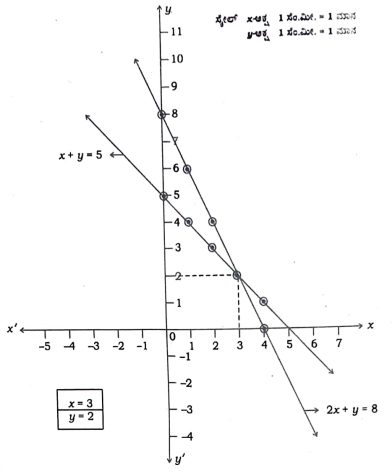
34. ಕೊಟ್ಟಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ, ನಕ್ಷೆಯ ವಿಧಾನದಿಂದ ಪರಿಹಾರ ಕಂಡುಹಿಡಿಯಿರಿ.
2x + y = 8
x + y = 5
ಉತ್ತರ:
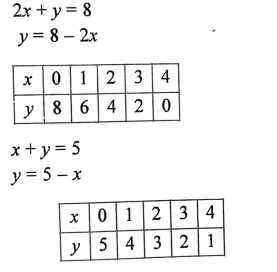
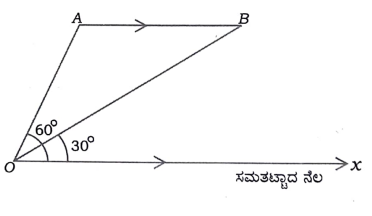
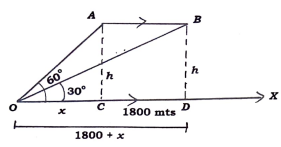
35. ಸಮತಟ್ಟಾದ ನೆಲಕ್ಕೆ ಸಮಾಂತರವಾಗಿ ಆಕಾಶದಲ್ಲಿ A ಬಿಂದುವಿನಿಂದ B ಬಿಂದುವಿನ ಮೂಲಕ ಹಾರುತ್ತಿರುವ ಒಂದು ವಿಮಾನವನ್ನು ನೆಲದ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಿನಿಂದ ವೀಕ್ಷಿಸಿದಾಗ À ಬಿಂದುವಿಗೆ ಉಂಟಾಗುವ ಉನ್ನತ ಕೋನವು 60° ಆಗಿದೆ. 10 ಸೆಕೆಂಡುಗಳ ನಂತರ ಇದೇ ವಿಮಾನವು B ಗೆ ತಲುಪಿದಾಗ ಉಂಟಾಗುವ ಉನ್ನತ ಕೋನವು 30° ಆಗಿರುತ್ತದೆ. ವಿಮಾನದ ವೇಗವು 648 ಕಿ.ಮೀ./ಗಂಟೆ ಆಗಿದ್ದಾಗ ನೆಲದ ಮೇಲಿನಿಂದ ಎಷ್ಟು ಎತ್ತರದಲ್ಲಿ ವಿಮಾನವು ಹಾರುತ್ತಿದೆ ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(√3 = 1.73 ಎಂದು ಉಪಯೋಗಿಸಿ)
ಉತ್ತರ:

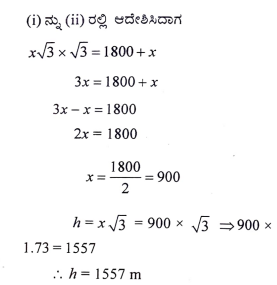
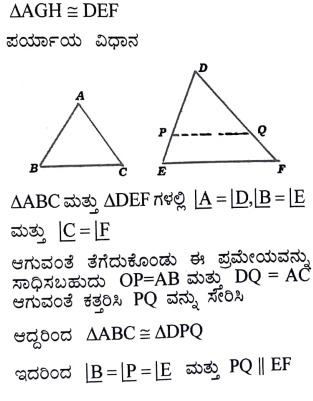
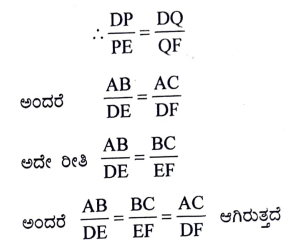
36. “ಎರಡು ತ್ರಿಭುಜಗಳಲ್ಲಿ ಅನುರೂಪ ಕೋನಗಳು ಸಮವಾದರೆ ಅವುಗಳ ಅನುರೂಪಬಾಹುಗಳ ಅನುಪಾತಗಳು ಸಮ (ಅಥವಾ ಸಮಾನುಪಾತದಲ್ಲಿರುತ್ತದೆ). ಆದ್ದರಿಂದ ಆ ತ್ರಿಭುಜಗಳು ಸಮರೂಪವಾಗಿರುತ್ತವೆ” ಎಂದು ಸಾಧಿಸಿ.
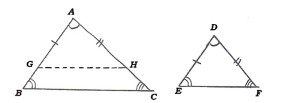
ಉತ್ತರ:


37. ಒಂದು ಔಷಧ ಕ್ಯಾನ್ಸುಲ್ನ ಆಕಾರವು ಒಂದು ಸಿಲಿಂಡರಿನ ಪ್ರತಿಪಾದಗಳಲ್ಲಿ ಒಂದೊಂದು ಅರ್ಧಗೋಳವನ್ನು ಅಂಟಿಸಿ ಮಾಡಿದೆ. ಕ್ಯಾನ್ಸುಲ್ನ ಸಂಪೂರ್ಣ ಉದ್ದವು 14ಮಿ.ಮೀ. ಮತ್ತು ಅದರ ವ್ಯಾಸವು 5 ಮಿ.ಮೀ. ಇದೆ. ಅದರ ಮೇಲೆ, ವಿಸ್ತೀರ್ಣವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
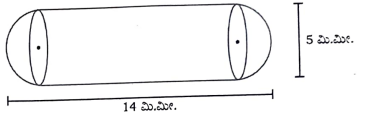
ಉತ್ತರ:
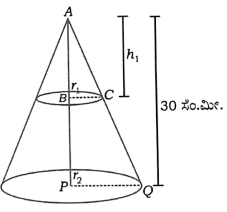

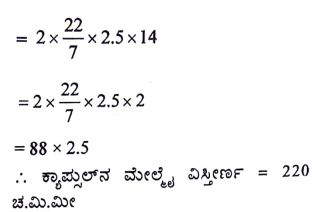
ಅಥವಾ
ಒಂದು ನೇರ ವೃತ್ತಾಪಾದ ಶಂಕುವಿನ ಎತ್ತರವು 30 ಸೆಂ.ಮೀ ಆಗಿದೆ. ಈ ಶಂಕುವನ್ನು ಅದರ ಪಾದಕ್ಕೆ ಸಮಾನಾಂತರವಾಗಿ ಅದರ ಶೃಂಗ ಬಿಂದುವಿನಿಂದ ಕೆಳಗೆ ಒಂದು ಸಮತಲದಿಂದ ಕತ್ತರಿಸಿ ತೆಗೆಯಲಾಗಿದೆ. ಈ ಶಂಕುವಿನ ಘನಫಲವು ದತ್ತ ಶಂಕುವಿನ ಘನಫಲದ 1/27 ರಷ್ಟಕ್ಕೆ ಸಮನಾಗಿದ್ದರೆ, ಶಂಕುವಿನ ಉಳಿದ ಭಾಗದ ಎತ್ತರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
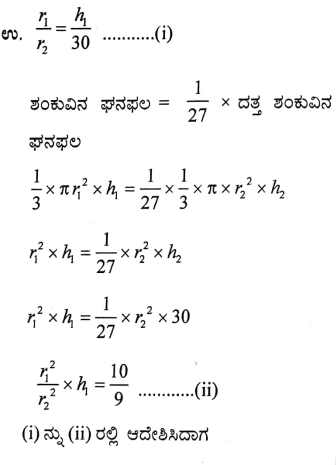

VI. ಈ ಕೆಳಗಿನ ಪ್ರಶ್ನೆಗೆ ಉತ್ತರಿಸಿ. 1 x 5 = 5
38. ಸಾಮಾನ್ಯ ವ್ಯತ್ಯಾಸವು ಸಮನಾಗಿರುವ ಎರಡು ವಿಭಿನ್ನ ಸಮಾರ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳಲ್ಲಿ ಮೊದಲನೇ ಶ್ರೇಢಿಯ ಮೊದಲನೇ ಪದವು ಎರಡನೇ ಶ್ರೇಢಿಯ ಮೊದಲನೇ ಪದಕ್ಕಿಂತ 3 ಹೆಚ್ಚಾಗಿದೆ. ಮೊದಲನೇ ಶ್ರೇಢಿಯ 7ನೇ ಪದವು 28 ಮತ್ತು ಎರಡನೇ ಶ್ರೇಢಿಯ 8ನೇ ಪದವು 29 ಆದಾಗ ಆ ಎರಡು ವಿಭಿನ್ನ ಸಮಾಂತರ ಶ್ರೇಢಿಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.