10th Standard Ganitiya Madarikarana Maths Notes Question Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, 10ನೇ ತರಗತಿ ಗಣಿತ ಗಣಿತೀಯ ಮಾದರೀಕರಣ ನೋಟ್ಸ್, 10th Class Maths Notes,10th Class Ganitiya Madarikarana notes pdf kannada medium all chapter maths notes, kseeb solutions for class 10 maths ganitiya madareekarana question answer, 10ನೇ ತರಗತಿ ಗಣಿತ ಪ್ರಶ್ನೋತ್ತರಗಳು pdf 10ನೇ ತರಗತಿ ಗಣಿತ ನೋಟ್ಸ್, 10th maths notes pdf in Kannada.
ಅನುಬಂಧ A2
ಗಣಿತೀಯ ಮಾದರೀಕರಣ
10ನೇ ತರಗತಿ ಗಣಿತ ಗಣಿತೀಯ ಮಾದರೀಕರಣ ನೋಟ್ಸ್
ಅಭ್ಯಾಸ A2.1
1. ಕೆಳಗಿನ ಸಂದರ್ಭವನ್ನು ಪರಿಗಣಿಸಿ. 13 ನೇ ಶತಮಾನದ ಆರಂಭದಲ್ಲಿ ರಚಿತವಾದ ಗಣಿತೀಯ ಸಮಸ್ಯೆ, ಲೆನಾರ್ಡ್ ಫಿಬೊನಾಚಿ ಕೇಳುತ್ತಾರೆ, ಆರಂಭದಲ್ಲಿ ಕೇವಲ ಎರಡು ಮೊಲಗಳಿದ್ದು, ಅವುಗಳ ಮೂಲಕ ವಂಶೋತ್ಪತ್ತಿಗೊಳಿಸುತ್ತಾ ಹೋದರೆ ಎಷ್ಟು ಮೊಲಗಳು ಉಂಟಾಗುತ್ತವೆ? ಒಂದು ಜೋಡಿ ಮೊಲಗಳು ಪ್ರತಿ ತಿಂಗಳು ಒಂದು ಜೋಡಿ ಸಂತತಿಯನ್ನುಂಟುಮಾಡುತ್ತವೆ ಮತ್ತು ಮೊಲಗಳ ಪ್ರತಿಯೊಂದು ಜೋಡಿಯೂ 2ನೇ ತಿಂಗಳಲ್ಲಿ ತಮ್ಮ ಪ್ರಥಮ ಸಂತತಿಯನ್ನುಂಟುಮಾಡುತ್ತದೆ ಎಂದು ಊಹಿಸಿಕೊಳ್ಳಿ. 0 ಮತ್ತು ಮೊದಲನೇ ತಿಂಗಳನ್ನು ಹೊರತುಪಡಿಸಿ, ಆ ಬಳಿಕ ಪ್ರತಿ ತಿಂಗಳಲ್ಲಿ ಉಂಟಾಗುವ ಮೊಲಗಳ ಜೋಡಿಗಳ ಸಂಖ್ಯೆಯು ಹಿಂದಿನ ಎರಡು ತಿಂಗಳಲ್ಲಿ ಉಂಟಾದ ಮೊಲಗಳ ಸಂಖ್ಯೆಯ ಮೊತ್ತಕ್ಕೆ ಸಮವಾಗಿರುತ್ತದೆ.
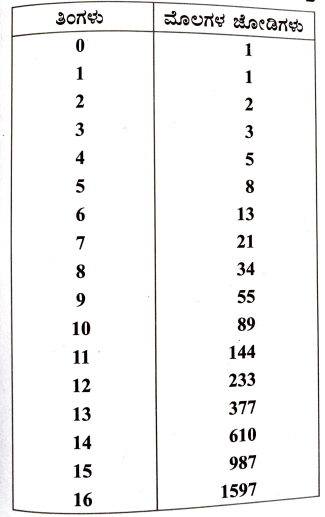
ಕೇವಲ 16 ತಿಂಗಳುಗಳಲ್ಲಿ, ಸುಮಾರು 1600 ಜೋಡಿ ಮೊಲಗಳು ಉಂಟಾಗುತ್ತವೆ! ಈ ಸಮಸ್ಯೆಯನ್ನು ಸ್ಪಷ್ಟವಾಗಿ ನಿರೂಪಿಸಿ ಮತ್ತು ಪ್ರಸ್ತುತ ಸಂದರ್ಭಕ್ಕೆ ಅನುಸಾರವಾಗಿ ಗಣಿತೀಯ ಮಾದರೀಕರಣದ ವಿವಿಧ ಹಂತಗಳನ್ನು ತಿಳಿಸಿ.
ಉತ್ತರ:
ಈ ಪ್ರಶ್ನೆಯನ್ನು ನಾವು ಫಿಬೊನಾಕಿ ಸರಣಿಯಿಂದ ಸಂಕ್ಷೇಪಿಸಬಹುದು. ಫಿಭೋನಾಕಿ ಸರಣಿ ಎಂದರೆ ಮೊದಲ ಎರಡು ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ ಎಂದು ಅರ್ಥ.
ಅಭ್ಯಾಸ A2.2
ಕೆಳಗಿನ ಪ್ರತಿಯೊಂದು ಸಮಸ್ಯೆಯನ್ನು ಬಿಡಿಸಲು ಬೇಕಾಗುವ ಗಣತೀಯ ಮಾದರೀಕರಣದ ವಿವಿಧ ಹಂತಗಳನ್ನು ಬರೆಯಿರಿ.
1. ಒಬ್ಬ ಪಕ್ಷಿತಜ್ಜೆಯು ಒಂದು ಪ್ರದೇಶದಲ್ಲಿರುವ ಗಿಳಿಗಳ ಸಂಖ್ಯೆಯನ್ನು ಅಂದಾಜಿಸಲು ಬಯಸುತ್ತಾರೆ. ಕೆಲವನ್ನು ಹಿಡಿಯಲು ಅವರು ಒಂದು ಬಲೆಯನ್ನು ಉಪಯೋಗಿಸುತ್ತಾರೆ ಹಾಗೂ 32 ಗಿಳಿಗಳನ್ನು ಹಿಡಿದು ಅವುಗಳಿಗೆ ಬಳೆಯನ್ನು ತೊಡಿಸಿ, ಬಿಟ್ಟು ಬಿಡುತ್ತಾರೆ. ಮುಂದಿನ ವಾರ ಇದೇ ರೀತಿ ಅವರು 40 ಗಿಳಿಗಳನ್ನು ಹಿಡಿಯುತ್ತಾರೆ. ಆದರೆ ಅವುಗಳಲ್ಲಿ 8 ಗಿಳಿಗಳು ಬಳೆಯನ್ನು ಹೊಂದಿರುತ್ತವೆ.
(i) ಅವರು ಎರಡನೇ ಸಲ ಹಿಡಿದ ಗಿಳಿಗಳ ಎಷ್ಟನೇ ಒಂದು ಅಂಶವು ಬಳೆಗಳನ್ನು ಹೊಂದಿತ್ತು.
ಉತ್ತರ:
1/5
(ii) ಆ ಪ್ರದೇಶದಲ್ಲಿದ್ದ ಒಟ್ಟು ಗಿಳಿಗಳ ಸಂಖ್ಯೆಯನ್ನು ಅಂದಾಜು ಮಾಡಿರಿ.
ಉತ್ತರ:
160
2. ಪಕ್ಕದಲ್ಲಿ ಕಾಣುತ್ತಿರುವುದು ಕಾಡಿನ ಒಂದು ವಿಹಂಗಮ ಛಾಯಚಿತ್ರ, ಇಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಚುಕ್ಕೆಯೂ ಒಂದು ಮರವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಪರಿಸರದ ಗಣತಿಯ ಒಂದು ಭಾಗವಾಗಿ, ನೀವು ಮಾಡಬೇಕಾದುದೆಂದರೆ ಈ ಪ್ರದೇಶದಲ್ಲಿರುವ ಮರಗಳ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು.
ಉತ್ತರ:
Icm² ಅಳತೆಯ ವಿಸ್ತೀರ್ಣವನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ ಮತ್ತು ಅದರಲ್ಲಿರುವ ಚುಕ್ಕಿಗಳನ್ನು ಎಣಿಸಿ. ಒಟ್ಟು ಮರಗಳ ಎಣಿಕೆಯು ಚುಕ್ಕಿಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
3. ಒಂದು ಟಿ.ವಿಯನ್ನು ₹24000 ನಗದು ಬೆಲೆಗೆ ಕೊಳ್ಳಬಹುದು ಅಥವಾ ₹8000 ನೇರ ನಗದು ಪಾವತಿ ಮಾಡಿ ತಲಾ ₹2800 ರ ಆರು ಮಾಸಿಕ ಕಂತುಗಳಲ್ಲಿ ಕೊಳ್ಳಬಹುದು. ಆಲಿಯವರು ₹8000 ದೊಂದಿಗೆ ಒಂದು ಟಿ.ವಿ ಯನ್ನು ಕೊಳ್ಳಲು ಮಾರುಕಟ್ಟೆಗೆ ತೆರಳಿದರು. ಅವರಿಗೆ ಈಗ ಎರಡು ಆಯ್ಕೆಗಳಿವೆ. ಒಂದನೆಯದು ಕಂತಿನ ಯೋಜನೆಯಡಿಯಲ್ಲಿ ಟಿ.ವಿಯನ್ನು ಖರೀದಿಸುವುದು ಅಥವಾ ಯಾವುದಾದರೂ ಆರ್ಥಿಕ ಸಹಕಾರ ಸಂಘದಿಂದ ಸಾಲ ಪಡೆದು ನಗದು ಪಾವತಿಯನ್ನು ಮಾಡುವುದು. ಸಹಕಾರ ಸಂಘವು ವಾರ್ಷಿಕ 18% ರ ದರದಲ್ಲಿ ಸರಳಬಡ್ಡಿಯನ್ನ ವಿಧಿಸುತ್ತದೆ. ಹಾಗಾದರೆ ಆಲಿಯವರಿಗೆ ಯಾವ ಆಯ್ಕೆಯು ಉತ್ತಮವಾಗಿದೆ?
ಉತ್ತರ:
ಮಾಸಿಕ ಕಂತಿನ ಬಡ್ಡಿದರವು 17.74% (18% ಗಿಂತ ಕಡಿಮೆ ಆಗಿದೆ).
ಅಭ್ಯಾಸ A2.3
1. ಕಳೆದ ಐದು ವರ್ಷಗಳ ದತ್ತಾಂಶಗಳನ್ನು ಆಧರಿಸಿ, ನಿಮ್ಮ ಶಾಲೆಯು ವರ್ಷದ ಕೊನೆಯಲ್ಲಿ ನಡೆಯುವ 10ನೇ ತರಗತಿಯ ಪಬ್ಲಿಕ್ ಪರೀಕ್ಷೆಯಲ್ಲಿ ಗಣಿತದಲ್ಲಿ ಪಡೆಯಬಹುದಾದ ಸರಾಸರಿ ಶೇಕಡಾವನ್ನು ಮುನ್ಸೂಚಿಸಲು ಪ್ರಯತ್ನಿಸಿ.
ಉತ್ತರ:
ವಿದ್ಯಾರ್ಥಿಗಳು ಶಿಕ್ಷಕರ ಸಹಿಪಡೆದು ಮೇಲಿನ ಪ್ರಶ್ನೆಯನ್ನು ಬಿಡಿಸಿ.
ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. ಗಣಿತೀಯ ಮಾದರೀಕರಣವು ಅತಿ ಹೆಚ್ಚು ಪ್ರಾಮುಖ್ಯತೆಯನ್ನು ಪಡೆದಿರುವ ಕೆಲವು ಉದಾಹರಣೆಗಳೆಂದರೆ,
- ತಲುಪಲುಸಾಧ್ಯವಾದ ಸ್ಥಳದಲ್ಲಿ ಒಂದು ನದಿಯ ಅಗಲ ಮತ್ತು ಆಳಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು.
- ಭೂಮಿ ಮತ್ತು ಇತರ ಗ್ರಹಗಳ ರಾಶಿಯನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
- ಭೂಮಿಯಿಂದ ಇತರ ಗ್ರಹಗಳಿಗಿರುವ ದೂರವನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
- ಒಂದು ದೇಶದಲ್ಲಿ ಮುಂಗಾರಿನ ಆಗಮನವನ್ನು ಊಹಿಸುವುದು.
- ಷೇರು ಮಾರುಕಟ್ಟೆಯ ಗತಿಯನ್ನು ಊಹಿಸುವುದು.
- ಒಬ್ಬ ವ್ಯಕ್ತಿಯ ದೇಹದೊಳಗಿನ ರಕ್ತದ ಪ್ರಮಾಣವನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
- ಒಂದು ನಗರದಲ್ಲಿ 10 ವರ್ಷಗಳ ನಂತರ ಆಗಬಹುದಾದ ಜನಸಂಖ್ಯೆಯನ್ನು ಊಹಿಸುವುದು.
- ಒಂದು ಮರದಲ್ಲಿರುವ ಎಲೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
- ಒಂದು ನಗರದ ವಾತಾವರಣದಲ್ಲಿರುವ ವಿವಿಧ ಮಾಲಿನ್ಯಕಾರಿಗಳ ppm ನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
- ಪರಿಸರದ ಮೇಲೆ ಮಾಲಿನ್ಯಕಾರಿಗಳ ಪರಿಣಾಮವನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
- ಸೂರ್ಯನ ಮೇಲ್ಟಿಯ ತಾಪವನ್ನು ಅಂದಾಜು ಮಾಡುವುದು.
2. ಗಣಿತೀಯ ಮಾದರೀಕರಣವನ್ನು ದೃಶ್ಯೀಕರಿಸುವ ವಿಧಾನ.
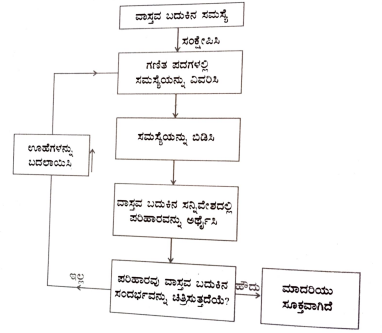
3. ಗಣಿತೀಯ ಮಾದರೀಕರಣವೆಂದರೆ, ಒಂದು ಸಮಸ್ಯೆಗೆ ಗಣಿತದ ಮಾದರಿಯನ್ನು ರಚಿಸುವ ವಿಧಾನವಾಗಿದ್ದು ಇದನ್ನು ಉಪಯೋಗಿಸಿ, ಸಮಸ್ಯೆಯನ್ನು ವಿಶ್ಲೇಷಿಸುವ ಮೂಲಕ ಅದನ್ನು ಬಿಡಿಸುವ ಒಂದು ಕ್ರಿಯೆ
4. ಗಣಿತೀಯ ಮಾದರೀಕರಣದಲ್ಲಿ, ನಾವು ವಾಸ್ತವ ಜಗತ್ತಿನ ಸಮಸ್ಯೆಯೊಂದನ್ನು ತೆಗೆದುಕೊಂಡು, ಸಮಾನವಾದ ಗಣಿತದ ಸಮಸ್ಯೆಯನ್ನಾಗಿ ಅದನ್ನು ಪರಿವರ್ತಿಸುತ್ತೇವೆ. ಆ ಬಳಿಕ ನಾವು ಗಣಿತದ ಸಮಸ್ಯೆಯನ್ನು ಬಿಡಿ ಅದರ ಪರಿಹಾರವನ್ನು ವಾಸ್ತವ ಜಗತ್ತಿನ ಸನ್ನಿವೇಶದಲ್ಲಿ ಪ್ರಸ್ತುತ ಪಡಿಸುತ್ತೇವೆ.
