10th Standard Bahupadoktigalu Maths Notes Question Answer Guide Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025 10ನೇ ತರಗತಿ ಗಣಿತ ಬಹುಪದೋಕ್ತಿಗಳು ನೋಟ್ಸ್ 10th Maths Notes Pdf 10ನೇ ತರಗತಿ ಗಣಿತ ನೋಟ್ಸ್ ಬಹುಪದೋಕ್ತಿಗಳು 10ನೇ ತರಗತಿ ಬಹುಪದೋಕ್ತಿಗಳು ಹತ್ತನೇ ತರಗತಿ kseeb solutions for class 10 maths in kannada bahupadoktigalu in kannada 10th notes 10th ಗಣಿತ ನೋಟ್ಸ್ bahupadoktigalu notes in kannada 10th standard.
ಭಾಗ – 2
ಘಟಕ 09 – ಬಹುಪದೋಕ್ತಿಗಳು
ಅಭ್ಯಾಸ 9.1
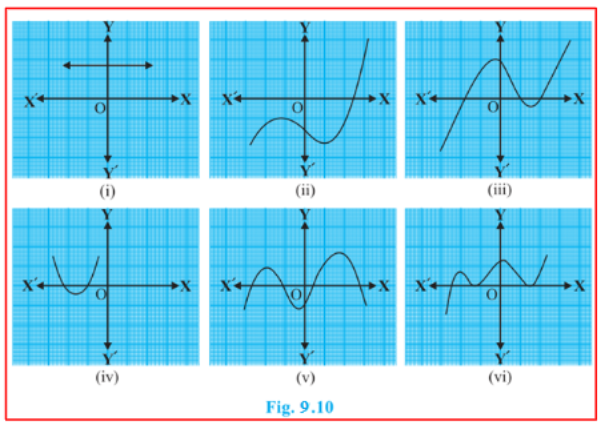
1. y = p(x) ದ ನಕ್ಷೆಗಳನ್ನು ಕೆಳಗೆ ಚಿತ್ರ 9.10ರಲ್ಲಿ ನೀಡಿದ್ದು, ಇಲ್ಲಿ (x) ಎಂಬುದು ಬಹುಪದೋಕ್ತಿಯಾಗಿದೆ. ಪ್ರತಿ ಸಂದರ್ಭದಲ್ಲಿಯೂ p(x) ದ ಶೂನ್ಯತೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
(i) ನಕ್ಷೆಯು x-ಅಕ್ಷವನ್ನು ಒಂದು ಬಿಂದುವಿನಲ್ಲೂ ಛೇದಿಸದೆ ಇರುವುದರಿಂದ, ಶೂನ್ಯತೆಗಳು ಸಂಖ್ಯೆ 0.
(ii) ನಕ್ಷೆಯು x-ಅಕ್ಷವನ್ನು ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಮಾತ್ರ ಛೇದಿಸುವುದರಿಂದ, ಶೂನ್ಯತೆಯ ಸಂಖ್ಯೆ 1.
(iii) ನಕ್ಷೆಯು x-ಅಕ್ಷವನ್ನು 3 ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವುದರಿಂದ. ಇಲ್ಲಿ ಶೂನ್ಯತೆಗಳ ಸಂಖ್ಯೆ 3.
(iv) ನಕ್ಷೆಯು x-ಅಕ್ಷವನ್ನು 2 ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವುದರಿಂದ, ಶೂನ್ಯತೆಗಳು ಸಂಖ್ಯೆ 2.
(v) ನಕ್ಷೆಯು x-ಆಕ್ಷವನ್ನು 4 ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವುದರಿಂದ. ಇಲ್ಲಿ ಶೂನ್ಯತೆಗಳು ಸಂಖ್ಯೆ 4.
(iv) ನಕ್ಷೆಯು x-ಅಕ್ಷವನ್ನು 3 ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವುದರಿಂದ. ಇಲ್ಲಿ ಶೂನ್ಯತೆಗಳು ಸಂಖ್ಯೆ 3.
ಅಭ್ಯಾಸ 9.2
1. ಈ ಕೆಳಗಿನ ವರ್ಗ ಬಹುಪದೋಕ್ತಿಗಳ ಶೂನ್ಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ ಹಾಗೂ ಶೂನ್ಯತೆಗಳು ಮತ್ತು ಸಹಗುಣಕಗಳ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ತಾಳೆ ನೋಡಿ.
(i) x2 – 2x – 8
ಉತ್ತರ:
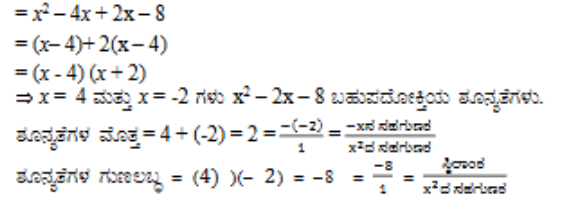
(ii) 4s2 – 4s – 1
ಉತ್ತರ:
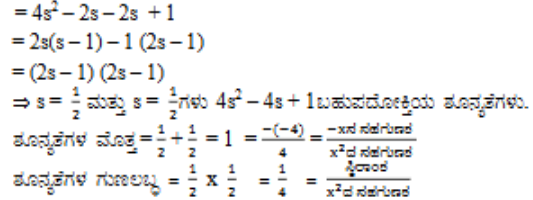
(iii) 6x2 – 3 – 7x
ಉತ್ತರ:
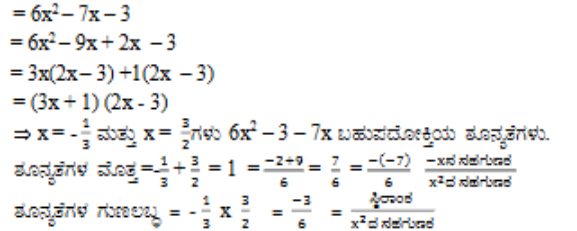
(iv) 4u2 + 8u
ಉತ್ತರ:
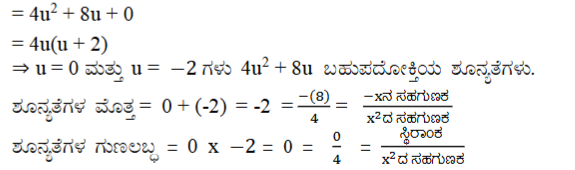
(v) t2 – 15
ಉತ್ತರ:

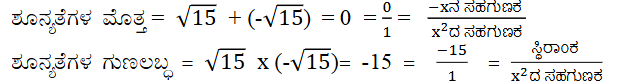
(vi) 3x2 – x – 4
ಉತ್ತರ:
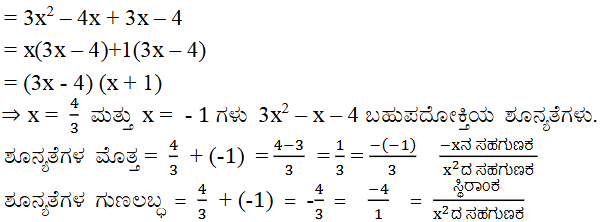
2. ಈ ಕೆಳಗಿನವುಗಳನ್ನು ಕ್ರಮವಾಗಿ ಶೂನ್ಯತೆಗಳ ಮೊತ್ತ ಹಾಗೂ ಗುಣಲಬ್ಧವನ್ನಾಗಿ ಹೊಂದಿರುವ ವರ್ಗ ಬಹುಪದೋಕ್ತಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
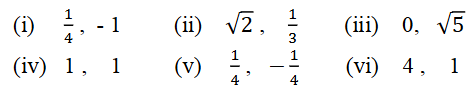
ಉತ್ತರ:

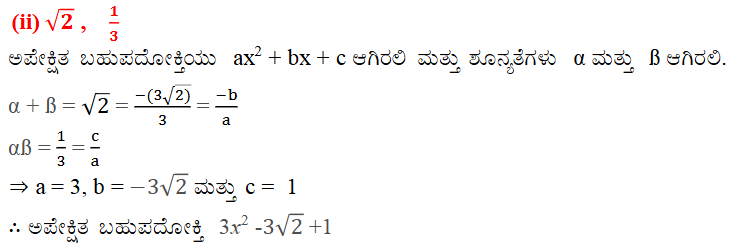

iv) 1, 1
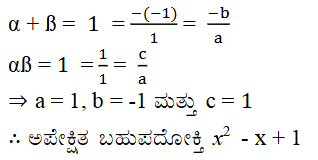
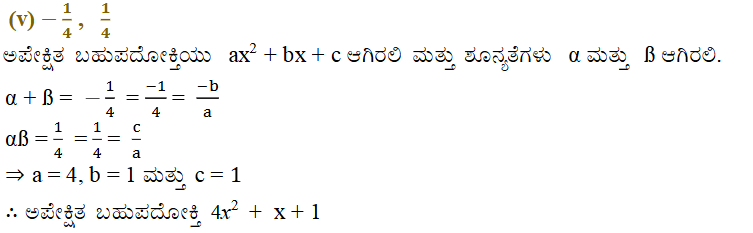
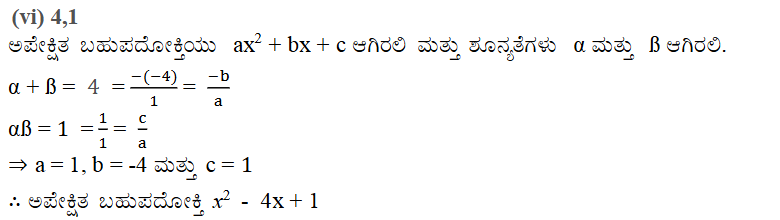
ಅಭ್ಯಾಸ 9.3
1. ಕೆಳಗಿನ ಪ್ರತಿಯೊಂದರಲ್ಲಿಯೂ ಬಹುಪದೋಕ್ತಿ p(x) ನ್ನು ಬಹುಪದೋಕ್ತಿ g(x) ದಿಂದ ಭಾಗಿಸಿ, ಭಾಗಲಬ್ಧ ಮತ್ತು ಶೇಷವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
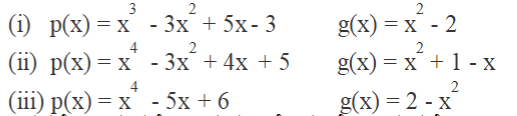
ಉತ್ತರ:

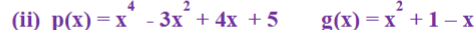


2. ಎರಡನೇ ಬಹುಪದೋಕ್ತಿಯನ್ನು ಮೊದಲನೇ ಬಹುಪದೋಕ್ತಿಯಿಂದ ಭಾಗಿಸಿ ಹಾಗೂ ಮೊದಲನೇ ಬಹುಪದೋಕ್ತಿಯು ಎರಡನೇ ಬಹುಪದೋಕ್ತಿಯ ಅಪವರ್ತನವಾಗಿದೆಯೇ ಎಂಬುದನ್ನು ಪರೀಕ್ಷಿಸಿ.
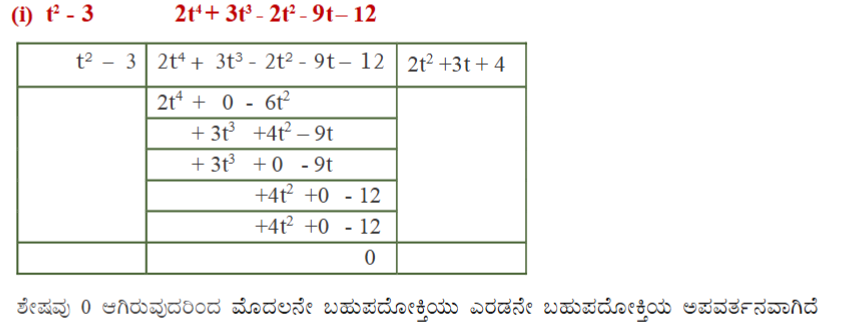
(i) t2-3, 2t4 + 3t3 – 2t2 – 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3 – 7x2 + 2x + 2
(iii) x3 – 3x + 1, x5 – 4x3 + x2 + 3x + 1
ಉತ್ತರ:
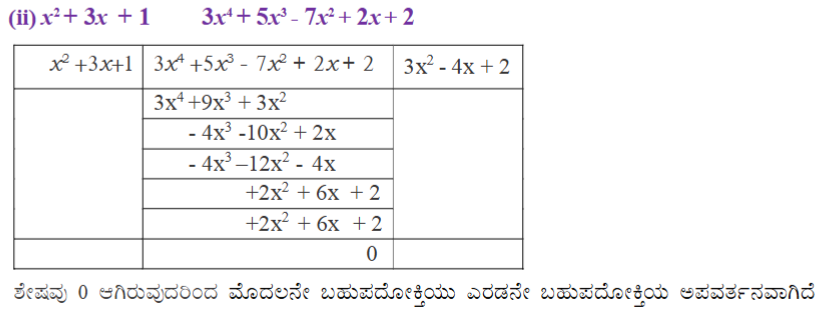
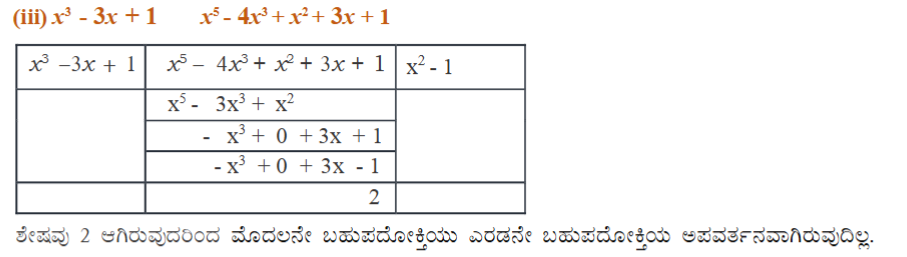
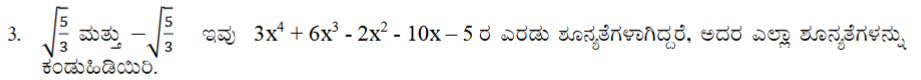
ಉತ್ತರ:


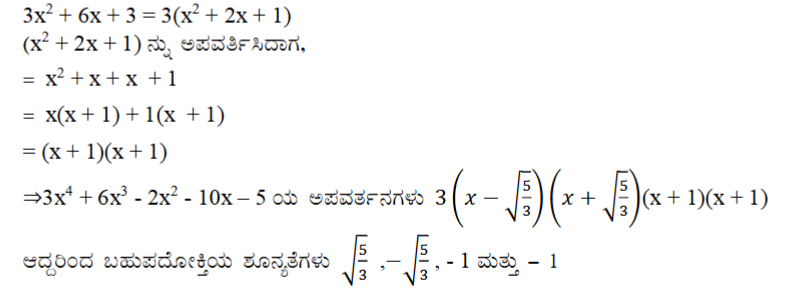
4. x3 – 3x2 + x + 2 ನ್ನು g(x) ಎಂಬ ಬಹುಪದೋಕ್ತಿಯಿಂದ ಭಾಗಿಸಿದಾಗ ಸಿಗುವ ಭಾಗಲಬ್ಧ ಮತ್ತು ಶೇಷಗಳು ಕ್ರಮವಾಗಿ x -2 ಮತ್ತು – 2x + 4 ಆದರೆ g(x) ನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
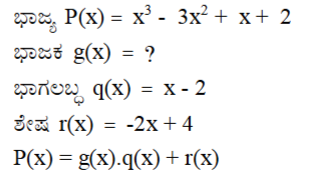
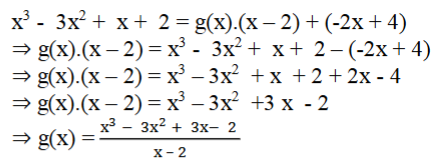
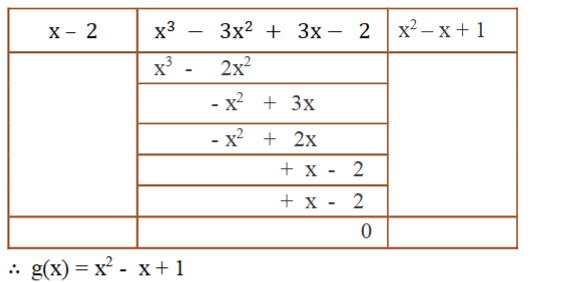
5. ಭಾಗಾಕಾರ ಕ್ರಮವಿಧಿಯನ್ನು ಹಾಗೂ ಈ ಕೆಳಗಿನ ಸಂಬಂಧಗಳನ್ನು ಸರಿದೂಗಿಸುವ p(x), g(x), q(x) ಮತ್ತು r(X) ಎಂಬ ಬಹುಪದೋಕ್ತಿಗಳಿಗೆ ಉದಾಹರಣೆಗಳನ್ನು ಕೊಡಿ.
(i) p(x) ನ ಡಿಗ್ರಿ = q(x) ನ ಡಿಗ್ರಿ
(ii) 2(x) ನ ಡಿಗ್ರಿ = r(x) ನ ಡಿಗ್ರಿ
(iii) r(x) ನ ಡಿಗ್ರಿ = 0
ಉತ್ತರ:

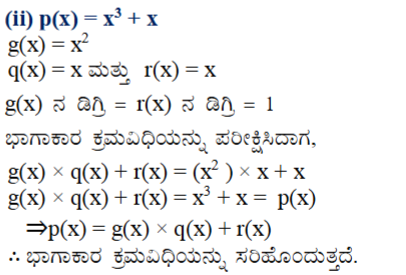
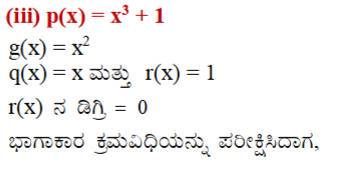
ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. ಡಿಗ್ರಿ 1 ಆಗಿರುವ ಬಹುಪದೋಕ್ತಿಗೆ ರೇಖಾತ್ಮಕ ಬಹುಪದೋಕ್ತಿ ಎನ್ನುತ್ತಾರೆ.
2. (x) ದಲ್ಲಿನ x ದ ಗರಿಷ್ಠ ಘಾತಸೂಚಿಯನ್ನು ಆ ಬಹುಪದೋಕ್ತಿ p(x) ದ ಮಹತ್ತಮ ಘಾತ ಅಥವಾ ಡಿಗ್ರಿ ಎನ್ನುತ್ತಾರೆ.
3. ಒಂದು ವರ್ಗ ಬಹುಪದೋಕ್ತಿ a + bx + c, a # ) ಯ ಶೂನ್ಯತೆಗಳು ನಿಖರವಾಗಿಯೂ ) = at + box + c ಯನ್ನು ಪ್ರತಿನಿಧಿಸುವ ಪರವಲಯವು x ನಿರ್ದೇಶಾಂಕಗಳಾಗಿರುತ್ತವೆ. ಅಕ್ಷವನ್ನು ಛೇದಿಸುವ ಬಿಂದುಗಳ *
4. ಡಿಗ್ರಿ 2 ಆಗಿರುವ ಬಹುಪದೋಕ್ತಿಯನ್ನು ವರ್ಗ ಬಹುಪದೋಕ್ತಿ ಎನ್ನುತ್ತಾರೆ.
5. ಡಿಗ್ರಿ 3 ಆಗಿರುವ ಬಹುಪದೋಕ್ತಿಯನ್ನು ಘನ ಬಹುಪದೋಕ್ತಿ ಎನ್ನುತ್ತಾರೆ.
6. ಸಾಮಾನ್ಯವಾಗಿ, x ಎಂಬ ಚರಾಕ್ಷರವುಳ್ಳ ಯಾವುದೇ ವರ್ಗ ಬಹುಪದೋಕ್ತಿಯು ax2 + bx + c ರೂಪದಲ್ಲಿರುತ್ತದೆ. ಇಲ್ಲಿ a. b, c ಗಳು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳಾಗಿದ್ದು, a ≠ 0 ಆಗಿದೆ.
7. ಸಾಮಾನ್ಯವಾಗಿ,nಡಿಗ್ರಿಯುಳ್ಳ ಒಂದು ಬಹುಪದೋಕ್ತಿ p(x)ನ್ನು ನೀಡಿದಾಗ y=p(x) ದನಕ್ಷೆಯು x – ಅಕ್ಷವನ್ನು ಗರಿಷ್ಠ n ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ n ಡಿಗ್ರಿಯುಳ್ಳ ಬಹುಪದೋಕ್ತಿಯು ಗರಿಷ್ಠ n ಶೂನ್ಯತೆಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.
8. ಸಾಮಾನ್ಯವಾಗಿ k ಯು ಒಂದು ವಾಸ್ತವ ಸಂಖ್ಯೆಯಾಗಿದ್ದು, p(k) = 0 ಆದರೆ k ಯನ್ನು ಬಹುಪದೋಕ್ತಿ p(x) ನ ಶೂನ್ಯತೆ ಎಂದು ಕರೆಯುತ್ತೇವೆ.
9. p(.x) ಮತ್ತು g(x) ಗಳು ಯಾವುದೇ ಎರಡು ಬಹುಪದೋಕ್ತಿಗಳಾಗಿದ್ದು, g(x) ≠ 0 ಆದಾಗ p(x) = g(x) x q(x) + r(x) ಆಗುವಂತೆ q(x) ಮತ್ತು r(x) ಎಂಬ ಬಹುಪದೋಕ್ತಿಗಳನ್ನು ನಾವು ಕಾಣಬಹುದು.
10. ಭಾಗಾಕಾರ ಕ್ರಮವಿಧಿಯ ಹೇಳಿಕೆಯು ಈ ಕೆಳಗಿನಂತಿದೆ.
ಯಾವುದೇ ದತ್ತ ಬಹುಪದೋಕ್ತಿ p(x) ಹಾಗೂ ಯಾವುದೇ ಶೂನ್ಯವಲ್ಲದ ಬಹುಪದೋಕ್ತಿ g(x) ಗಳಿಗೆ p(x) = g(x) q(x) + r(x) ಆಗುವಂತೆ q(x) ಮತ್ತು r(x) ಎಂಬ ಎರಡು ಬಹುಪದೋಕ್ತಿಗಳಿರುತ್ತವೆ. ಇಲ್ಲಿ r(x) = 0 ಅಥವಾ r(x) ದ ಡಿಗ್ರಿ < g(x) ದ ಡಿಗ್ರಿ ಆಗಿರುತ್ತದೆ.
11.
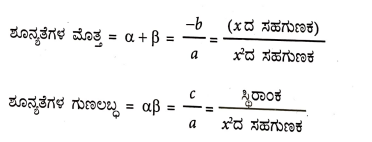
ಇತರೆ ವಿಷಯಗಳು :
10ನೇ ತರಗತಿ ಗಣಿತ ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ನೋಟ್ಸ್
10ನೇ ತರಗತಿ ಗಣಿತ ವರ್ಗ ಸಮೀಕರಣಗಳು ನೋಟ್ಸ್
