10th Standard Vruttagalu Maths Notes Question Answer Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, 10th maths vruttagalu in kannada, ವೃತ್ತಗಳು ಪಾಠ 10th, 10ನೇ ತರಗತಿ ಗಣಿತ ವೃತ್ತಗಳು ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು, ವೃತ್ತಗಳು 10th notes, 10th ಗಣಿತ ನೋಟ್ಸ್, kseeb solutions for class 10 maths chapter 4 notes in kannada medium, 10th class maths chapter 4 in kannada medium, 10th class maths 4th lesson notes state syllabus, 10th standard maths notes, sslc maths chapter 4 in kannada.
ಘಟಕ 04 – ವೃತ್ತಗಳು
10ನೇ ತರಗತಿ ಗಣಿತ ವೃತ್ತಗಳು ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು
ಅಭ್ಯಾಸ 4.1
1. ವೃತ್ತವು ಹೊಂದಿರಬಹುದಾದ ಸ್ಪರ್ಶಕಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು?
ಉತ್ತರ: ಅಪರಿಮಿತ.
2. ಬಿಟ್ಟ ಸ್ಥಳ ತುಂಬಿರಿ:
(i) ವೃತ್ತವನ್ನು ಸ್ಪರ್ಶಕವೊಂದು ಛೇದಿಸುವ ಬಿಂದುಗಳ ಸಂಖ್ಯೆ ____________
ಉತ್ತರ: ಒಂದು
(ii) ವೃತ್ತವನ್ನು ಎರಡು ಬಿಂದುಗಳಲ್ಲಿ ಛೇದಿಸುವ ರೇಖೆಯೇ ____________
ಉತ್ತರ: ಛೇದಕ
iii) ಒಂದು ವೃತ್ತವು ಹೊಂದಿರಬಹುದಾದ ಸಮಾಂತರ ಸ್ಪರ್ಶಕಗಳ ಗರಿಷ್ಟ ಸಂಖ್ಯೆ ___________
ಉತ್ತರ: ಅಪರಿಮಿತ
(iv) ಒಂದು ವೃತ್ತ ಸ್ಪರ್ಶಕ ಮತ್ತು ಒಂದು ವೃತ್ತ ಹೊಂದಿರುವ ಸಾಮಾನ್ಯ ಬಿಂದುವೇ ____________
ಉತ್ತರ: ಸ್ಪರ್ಶಬಿಂದು
3. 5 cm ತ್ರಿಜ್ಯವಿರುವ ವೃತ್ತಕ್ಕೆ P ಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ಸ್ಪರ್ಶಕ PQ. ಇದು ವೃತ್ತಕೇಂದ್ರ O ದಿಂದ ಎಳೆದ ರೇಖೆಯನ್ನು Q ಬಿಂದುವಿನಲ್ಲಿ ಸಂಧಿಸುತ್ತದೆ. OQ = 12 cm ಆದರೆ PQ ಉದ್ದವು
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) √119 cm
ಉತ್ತರ:

(D) √119 cm
4. ವೃತ್ತವನ್ನು ರಚಿಸಿ. ಕೊಟ್ಟಿರುವ ರೇಖೆಗೆ ಸಮಾಂತರವಾಗಿರುವಂತೆ ವೃತ್ತಕ್ಕೆ ಒಂದು ರೇಖೆಯು ಸ್ಪರ್ಶಕ ಮತ್ತೊಂದು ರೇಖೆಯು ಛೇದಕವಾಗಿರುವಂತೆ ಎರಡು ರೇಖೆಗಳನ್ನು ಎಳೆಯಿರಿ.
ಉತ್ತರ:
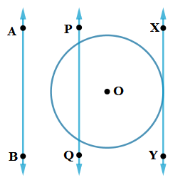
AB – ಒಂದು ರೇಖೆ
PQ – ಒಂದು ಛೇದಕ
XY – ಒಂದು ಸ್ಪರ್ಶಕ
ಅಭ್ಯಾಸ 4.2
ಪ್ರಶ್ನೆ 1 ರಿಂದ 3 ರವರೆಗೆ ಸರಿಯಾದ ಆಯ್ಕೆಯನ್ನು ಆರಿಸಿ ಮತ್ತು ಉತ್ತರವನ್ನು ಸಮರ್ಥಿಸಿರಿ.
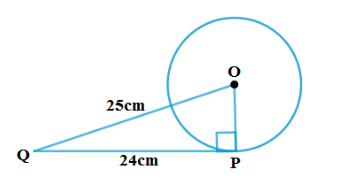
1. ಒಂದು ಬಿಂದು Q ದಿಂದ, ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕದ ಉದ್ದವು 24 cm ಮತ್ತು ವೃತ್ತಕೇಂದ್ರ ಹಾಗೂ Q ಬಿಂದು ನಡುವಿನ ದೂರ 25 cm ಆದರೆ ವೃತ್ತದ ತ್ರಿಜ್ಯವು
(A) 7 cm
B) 12 cm
(C) 15 cm
(D) 24.5 cm
ಉತ್ತರ:

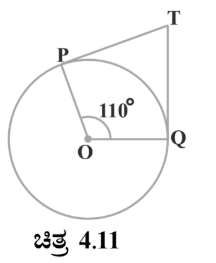
2. ಚಿತ್ರ 4.11 ರಲ್ಲಿ ∠POQ 110°, ಆಗಿರುವಂತೆ, O ಕೇಂದ್ರವುಳ್ಳ ವೃತ್ತಕ್ಕೆ TP ಮತ್ತು TQ ಸ್ಪರ್ಶಕಗಳಾಗಿವೆ. ಹಾಗಾದರೆ ∠PTQ ದ ಅಳತೆಯು
(A) 60°
(B) 70°
(C) 80°
(D) 90°
ಉತ್ತರ:
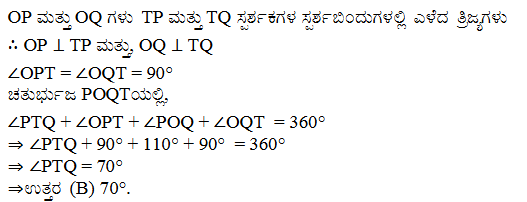
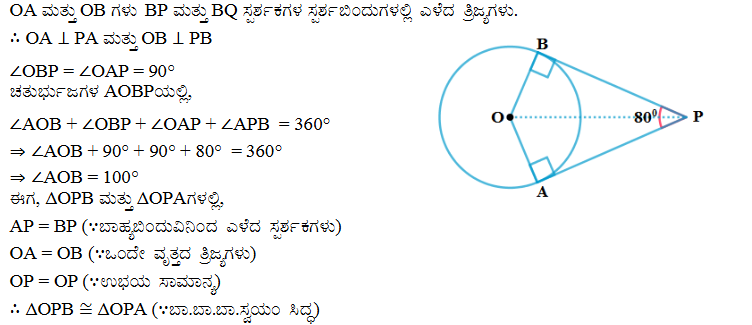
3 ‘0’ ವೃತ್ತಕೇಂದ್ರವಿರುವ ಒಂದು ವೃತ್ತಕ್ಕೆ P ಬಿಂದುವಿನಿಂದ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳಾದ PA ಮತ್ತು PB ಗಳ ನಡುವಿನ ಕೋನ 80° ಆದರೆ POA ದ ಅಳತೆಯು
(A) 50°
(B) 60°
(C) 70°
(D) 80°
ಉತ್ತರ: (A) 50°
ಸಮರ್ಥನೆ
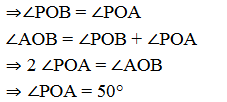
4. ಒಂದು ವೃತ್ತಕ್ಕೆ ವ್ಯಾಸದ ಅಂತ್ಯ ಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿವೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
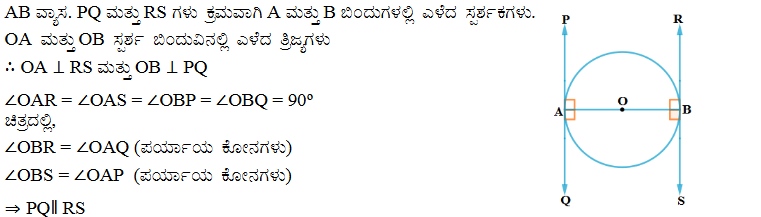
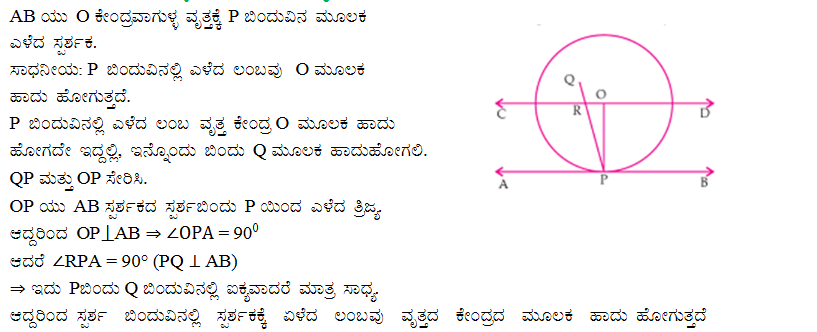
5. ಸ್ಪರ್ಶ ಬಿಂದುವಿನಲ್ಲಿ ಸ್ಪರ್ಶಕಕ್ಕೆ ಎಳೆದ ಲಂಬವು ವೃತ್ತದ ಕೇಂದ್ರದ ಮೂಲಕ ಹಾದು ಹೋಗುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
6. ವೃತ್ತ ಕೇಂದ್ರದಿಂದ 5 cm ದೂರದಲ್ಲಿರುವ ೦ ಬಿಂದುವಿನಿಂದ ಎಳೆದ ಸ್ಪರ್ಶಕದ ಉದ್ದವು 4 cm ಇದೆ ವೃತ್ತದ ತ್ರಿಜ್ಯದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

7. ಎರಡು ಏಕಕೇಂದ್ರಿಯ ವೃತ್ತಗಳ ತ್ರಿಜ್ಯಗಳು 5 cm ಮತ್ತು 3 cm ಆಗಿವೆ. ಚಿಕ್ಕ ವೃತ್ತಕ್ಕೆ ಸ್ಪರ್ಶಿಸುವಂತೆ ದೊಡ್ಡ ವೃತ್ತದ ಬ್ಯಾದ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
0 ವನ್ನು ಕೇಂದ್ರ ಬಿಂದುವನ್ನಾಗಿರಿಸಿಕೊಂಡು 5 cm ಮತ್ತು 3 cm ನ್ನು ತ್ರಿಜ್ಯವನ್ನಾಗಿರಿಸಿಕೊಂಡು ಎರಡು ಏಕಕೇಂದ್ರೀಯ ವೃತ್ತಗಳನ್ನು ರಚಿಸಿ ಮತ್ತು Pಬಿಂದುವಿನಲ್ಲಿ AB ಜ್ಞಾವನ್ನು ಎಳೆಯಿರಿ.
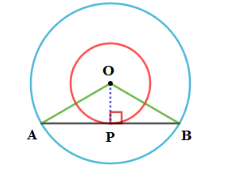
ರಚನೆ: OP ಮತ್ತು OB ಯನ್ನು ಸೇರಿಸಿ
ಪರಿಹಾರ:
OP = 3 cm (ಚಿಕ್ಕ ವೃತ್ತದ ತಿಜ್ಞ)
OB = 5 cm (ದೊಡ್ಡ ವೃತ್ತದ ತಿಜ್ಞ)
ΔΟΡΗ ಯಲ್ಲಿ
∠OPB = 90°
(ವೃತ್ತದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ಸ್ಪರ್ಶಕವು ಸ್ಪರ್ಶಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ತ್ರಿಜ್ಯಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ)
ಪೈಥಾಗೊರಸ್ನ ಪ್ರಮೇಯದಂತೆ
OB2 = OP2 + PB2
52 = 32 + PB2
PB2 =25 – 9 → PB2 16 = 4cm
AB = AP + PB = 4 + 4 = 8cm
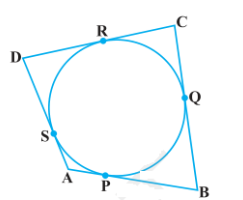
8. ABCD ಚತುರ್ಭುಜದಲ್ಲಿ ವೃತ್ತವು ಅಂತಸ್ಥವಾಗಿದೆ. (ಚಿತ್ರ 4.12 ನೋಡಿ). AB + CD =AD +BC ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
ABCD ಚತುರ್ಭುಜದಲ್ಲಿ ವೃತ್ತವು ಅಂತಸ್ಥವಾಗಿದೆ.
ಸಾಧನೀಯ: AB + CD = AD + BC
ಸಾಧನೆ: AP = AS……. (1) ಬಾಹ್ಯಬಿಂದುವಿನಿಂದ
BP = BQ ……(2) ವೃತ್ತಕ್ಕೆ ಎಳೆದ
CR = CQ ……(3) ಎರಡು ಸ್ಪರ್ಶಕಗಳು
DR = DS ….. (4) ಸಮವಾಗಿರುತ್ತದೆ
AP + BP + CR + DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
AB + CD = AD + BC
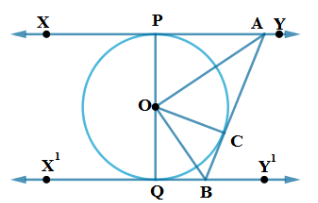
9. ಚಿತ್ರ 4.13 ರಲ್ಲಿ, ‘O’ ವೃತ್ತ ಕೇಂದ್ರ ಹೊಂದಿರುವ ಒಂದು ವೃತ್ತಕ್ಕೆ XY ಮತ್ತು N’Y’ ಸಮಾಂತರ ಸ್ಪರ್ಶಕಗಳಾಗಿದೆ ಮತ್ತು ಸ್ಪರ್ಶ ಬಿಂದು C ನಲ್ಲಿ ಎಳೆದ ಮತ್ತೊಂದು ಸ್ಪರ್ಶಕ AB ಯು XY ಅನ್ನು A ಬಿಂದುವಿನಲ್ಲಿ ಮತ್ತು X’Y’ ಅನ್ನು B ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ. ಹಾಗಾದರೆ ∠AOB = 90° ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
ದತ್ತ: ವೃತ್ತ ಕೇಂದ್ರ ‘O’ ಯಿಂದ ರಚಿಸಿದ ವೃತ್ತಕ್ಕೆ XY ಮತ್ತು X’Y’ ಗಳೆರಡು ಸಮಾಂತರ ಸ್ಪರ್ಶಕಗಳು ಹಾಗೂ ಸ್ಪರ್ಶದಿಂದು C ನಲ್ಲಿ ಎಳೆದ ಮತ್ತೊಂದು ಸ್ಪರ್ಶಕ್ಕೆ AB ಯು XY ಅನ್ನು A ಬಿಂದುವಿನಲ್ಲಿ ಮತ್ತು ಬಿಂದುವಿನಲ್ಲಿ ಛೇಡಿಸುತ್ತದೆ.
ಸಾಧನೀಯ: ∠AOB =90°
ರಚನೆ: OC ಯನ್ನು ಸೇರಿಸಿ.
ಸಾಧನೆ: ΔOPA ಮತ್ತು ΔOCA
OP= OC (ಒಂದೇ ವೃತ್ತದ ತ್ರಿಜ್ಯಗಳು)
OA OA (ಸಾಮಾನ್ಯ ಬಾಹು)
AP = AC (ಬಾಹ್ಯಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳು ಸಮವಾಗಿರುತ್ತದೆ.)
ΔОРА ≅ ΔОСА ( ಬಾಬಾಬಾ ಸಿದ್ಧಾಂತದನ್ವಯ)
∠POA = ∠COA (ಸ.ತ್ರಿ.ಅ.ಬಾ) …..(1)
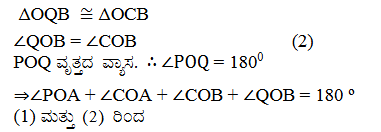
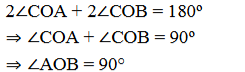
10. ಬಾಹ್ಯ ಬಿಂದುವಿನಿಂದ ಒಂದು ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಎರಡು ಸ್ಪರ್ಶಕಗಳ ನಡುವಿನ ಕೋನ ಹಾಗೂ ಸ್ಪರ್ಶ ಬಿಂದುಗಳನ್ನು ವೃತ್ತಕೇಂದ್ರಕ್ಕೆ ಸೇರಿಸುವಂತೆ ಎಳೆದ ರೇಖಾಖಂಡಗಳ ನಡುವಿನ ಕೋನಗಳು ಪರಿಪೂರಕಗಳಾಗಿರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
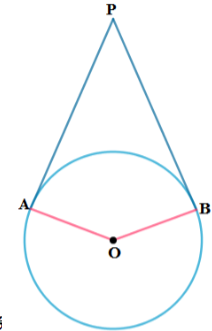
‘O’ ವೃತ್ತಕೇಂದ್ರದಿಂದ ರಚಿಸಿದ ವೃತ್ತಕ್ಕೆ PA ಮತ್ತು PB ಗಳು ಬಾಹ್ಯಬಿಂದು ‘P ಯಿಂದ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳು,
ಸಾಧನೆ: ∠OAP = ∠OBP =90º
(ವೃತ್ತದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ಸ್ಪರ್ಶಕವು ಸ್ಪರ್ಶಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ತ್ರಿಜ್ಯಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ)
∠OAP + ∠APB + ∠OBP + AOP = 360º
90º + ∠APB + 90º + ∠AOB = 360º
∠APB + ∠AOB = 360º -180º
∠APB + ∠AOB = 180º
11. ಒಂದು ಸಮಾಂತರ ಚತುರ್ಭುಜದಲ್ಲಿ ವೃತ್ತವು ಅಂತಸ್ಥವಾದಾಗ ಸಮಾಂತರ ಚತುರ್ಭುಜವು ವಜ್ರಾಕೃತಿಯಾಗುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
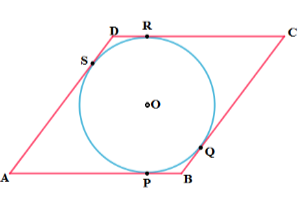
DR = DS
CR = CQ
BP = BQ
AP = AS
ಬಾಹ್ಯಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳು ಸಮವಾಗಿರುತ್ತವೆ.
DR + CR + BP + AP =DS + CQ + BQ + AS
(DR + CR) + (BP + AP) =(DS + AS) + (CQ + BQ)
CD + AB = AD + BC
2AB = 2BC
AB = BC
AB = BC = CD = DA
ABCD ಯು ಒಂದು ವಜ್ರಾಕೃತಿ
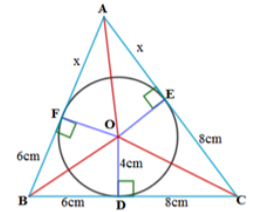
12. ಸ್ಪರ್ಶ ಬಿಂದು D ಯು BC ಬಾಹುವನ್ನು BD ಮತ್ತು DC ಯ ಉದ್ದ ಕ್ರಮವಾಗಿ 8 cm ಮತ್ತು 6 cm ಇರುವಂತೆ 4 cm ತ್ರಿಜ್ಯವಿರುವ ಒಂದು ವೃತ್ತವು ΔABC ಯಲ್ಲಿ ಆವೃತ್ತಗೊಳಿಸಲು ಅಂತಸ್ಥವಾಗಿರುವಂತೆ ರಚಿಸಲಾಗಿದೆ. [ ಚಿತ್ರ 4.14 ನೋಡಿ] AB ಮತ್ತು AC ಬಾಹುಗಳ ಉದ್ದವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ
CD = CF =6 cm (C ಬಾಹ್ಯದಿಂದ)
BD = BE = 8 cm ( B ಬಾಹ್ಯದಿಂದ )
AF = AE = x cm ( A ಬಾಹ್ಯದಿಂದ )
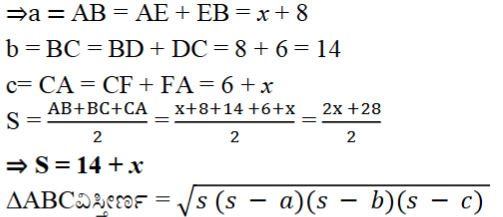

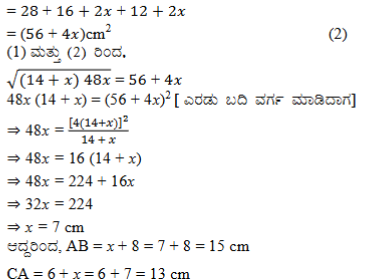
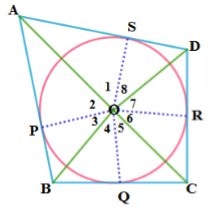
13. ಒಂದು ಚತುರ್ಭುಜದಲ್ಲಿ ವೃತ್ತವು ಅಂತಸ್ಥವಾದಾಗ, ವೃತ್ತದ ಕೇಂದ್ರದಲ್ಲಿ ಚತುರ್ಭುಜದ ಅಭಿಮುಖ ಬಾಹುಗಳಿಂದ ಉಂಟಾದ ಕೋನಗಳು ಪರಿಪೂರಕಗಳಾಗಿರುತ್ತದೆ ಎಂದು ಸಾಧಿಸಿ.
ಉತ್ತರ:
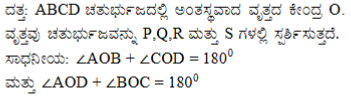

ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. ವೃತ್ತದ ಮೇಲಿನ ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ವೃತ್ತಕ್ಕೆ ಒಂದೇ ಒಂದು ಸ್ಪರ್ಶಕ ಮಾತ್ರ ಎಳೆಯಬಹುದು.
2. ಒಂದು ವೃತ್ತದಲ್ಲಿ, ಒಂದು ರೇಖೆಯ ಎರಡು ಸಾಮಾನ್ಯ ಬಿಂದುಗಳಿದ್ದರೆ ಅದು ಛೇದಕ ರೇಖೆ.
3. ಸ್ಪರ್ಶಕ ಮತ್ತು ವೃತ್ತಕ್ಕಿರುವ ಸಾಮಾನ್ಯ ಬಿಂದುವನ್ನು ಸ್ಪರ್ಶ ಬಿಂದು ಎಂದು ಕರೆಯುತ್ತಾರೆ.
4. ವೃತ್ತವನ್ನು ಒಂದೇ ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುವ ರೇಖೆಯನ್ನು ಸ್ಪರ್ಶಕ
5. ಸ್ಪರ್ಶ ಬಿಂದುವಿನಲ್ಲಿ ತ್ರಿಜ್ಯವನ್ನು ಹೊಂದಿರುವ ರೇಖೆಯನ್ನು ಕೆಲವು ಸಲ ಒಂದು ಬಿಂದುವಿನ ವೃತ್ತದ “ಲಂಬಕ’ ಎಂದು ಕರೆಯುತ್ತೇವೆ.
6. ವೃತ್ತದ ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಒಂದೇ ಒಂದು ಸ್ಪರ್ಶಕವಿದೆ.
7. ವೃತ್ತದ ಮೇಲಿನ ಯಾವುದೇ ಬಿಂದುವಿನಲ್ಲಿ ಎಳೆದ ಸ್ಪರ್ಶಕವು, ಸ್ಪರ್ಶ ಬಂದುವಿನಲ್ಲಿ ಎಳೆದ ತ್ರಿಜ್ಯಕ್ಕೆ ಲಂಬವಾಗಿರುತ್ತದೆ.
8. ಎರಡು ಎಕಕೇಂದ್ರೀಯ ವೃತ್ತಗಳಲ್ಲಿ, ದೊಡ್ಡ ವೃತ್ತದ ಜ್ಯಾವು ಚಿಕ್ಕ ವೃತ್ತವನ್ನು ಸ್ಪರ್ಶಿಸಿದರೆ, ಜ್ಯಾವು ಸ್ಪರ್ಶ ಬಿಂದುವಿನಲ್ಲಿ ದ್ವಿಭಾಗವಾಗುತ್ತದೆ.
9. ಬಾಹ್ಯ ಬಿಂದುವಿನಿಂದ ವೃತ್ತಕ್ಕೆ ಎಳೆದ ಸ್ಪರ್ಶಕಗಳ ಉದ್ದವು ಸಮನಾಗಿರುತ್ತದೆ.
ಭೇದಕವೊಂದರ ಅನುರೂಪ ಪ್ಯಾದ ಎರಡು ಅಂತ್ಯ ಬಿಂದುಗಳ ಏಕ್ಯವಾದಾಗ ದೊರೆಯುವ ಛೇದಕದ ವಿಶೇಷ ಪ್ರಕರಣವೇ ವೃತ್ತ ಸ್ಪರ್ಶಕ
ವೃತ್ತ ಎಂದರೆ ಒಂದು ಸಮತಲದಲ್ಲಿ ಸ್ಥಿರ ಬಿಂದು.
ಇತರೆ ವಿಷಯಗಳು :
ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು ನೋಟ್ಸ್
ವೃತ್ತಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ವಿಸ್ತೀರ್ಣಗಳು ನೋಟ್ಸ್
