10th Standard Eradu Charaksharagaliruva Rekhatmaka Samikaranagala Jodigalu Maths Notes Question Answers Guide Extract Mcq Pdf Download in Kannada Medium Karnataka State Syllabus 2025, 10ನೇ ತರಗತಿ ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು ಗಣಿತ ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು, 10th standard maths 3rd chapter notes in kannada medium, kseeb solutions for class 10 maths chapter 3 in kannada, maths notes for class 10 pdf, 10ನೇ ತರಗತಿ ಗಣಿತ ನೋಟ್ಸ್, 10th class maths 3rd lesson notes state syllabus, 10th standard maths notes, ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳು pdf, sslc maths chapter 3 notes Pdf Download.
ಘಟಕ 03 – ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು
10ನೇ ತರಗತಿ ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು ಗಣಿತ ನೋಟ್ಸ್
ಅಭ್ಯಾಸ 3.1
1. ಆಫ್ತಾಬ್ ತಮ್ಮ ಮಗಳಲ್ಲಿ ಹೇಳುತ್ತಾರೆ, “ಎಳು ವರ್ಷಗಳ ಹಿಂದೆ ಆಗಿನ ನಿನ್ನ ವಯಸ್ಸಿಗಿಂತ ನನ್ನ ವಯಸ್ಸು ಏಳು ಪಟ್ಟು ಹೆಚ್ಚಾಗಿತ್ತು. ಇನ್ನು ಮೂರು ವರ್ಷಗಳ ಬಳಿಕ ಕೂಡಾ ಆವತ್ತಿನ ನಿನ್ನ ವಯಸ್ಸಿಗಿಂತ ನನ್ನ ವಯಸ್ಸು ಮೂರು ಪಟ್ಟು ಹೆಚ್ಚಾಗುತ್ತದೆ”. (ಈ ಸಂಗತಿಯು ಆಸಕ್ತಿದಾಯಕವಲ್ಲವೆ!) ಈ ಸಂದರ್ಭವನ್ನು ಬೀಜಗಣಿತೀಯವಾಗಿ ಮತ್ತು ರೇಖಾಗಣಿತೀಯವಾಗಿ ಪ್ರತಿನಿಧಿಸಿ.
ಉತ್ತರ:
ಅಫ್ತಾಬ್ನ ವಯಸ್ಸು = x ವರ್ಷಗಳಾಗಿರಲಿ
ಅವನ ಮಗಳ ವಯಸ್ಸು = y ವರ್ಷಗಳಾಗಿರಲಿ
ಏಳು ವರ್ಷಗಳ ಹಿಂದೆ ಅಫ್ತಾಬ್ನ ವಯಸ್ಸು =(x-7) ಅ
ವನ ಮಗಳ ವಯಸ್ಸು = (y-7)
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ ಅಫ್ತಾಬ್ನ ವಯಸ್ಸು =7 (ಅವನ ಮಗಳ ವಯಸ್ಸು)
(x – 7) = 7(y – 7)
x – 7 = 7y – 49
x – 7y + 42 = 0 (i)
ಮೂರು ವರ್ಷಗಳ ನಂತರ,
ಅಫ್ತಾಬ್ನ ವಯಸ್ಸು = x + 3 ವರ್ಷಗಳು
ಅವನ ಮಗಳ ವಯಸ್ಸು = y + 3 ವರ್ಷಗಳು
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ
x + 3 = 3( y + 3)
x + 3 = 3y + 9
x – 3y – 6 = 0 (ii)
ಆದ್ದರಿಂದ ಬೀಜಗಣಿತೀಯವಾಗಿ
x – 7y = – 42
x – 3y = 6
x – 7y = – 42ಗೆ
x = – 42 + 7y

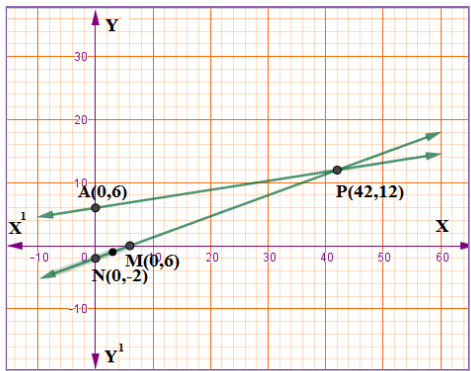
2. ಒಂದು ಕ್ರಿಕೆಟ್ ತಂಡದ ತರಬೇತುಗಾರ್ತಿ 3 ಬ್ಯಾಟ್ಗಳು ಮತ್ತು 6 ಚೆಂಡುಗಳನ್ನು ₹3900 ಕೈ ಕೊಳ್ಳುತ್ತಾರೆ. ಆ ಬಳಿಕ ಅದೇ ರೀತಿಯ ಇನ್ನೊಂದು ಬ್ಯಾಟ್ ಮತ್ತು ಇನ್ನೂ 3 ಚೆಂಡುಗಳನ್ನು ₹1300ಕ್ಕೆ ಕೊಳ್ಳುತ್ತಾರೆ. ಈ ಸಂದರ್ಭವನ್ನು ಬೀಜಗಣಿತೀಯವಾಗಿ ರೇಖಾಗಣಿತೀಯವಾಗಿ ಪ್ರತಿನಿಧಿಸಿ.
ಉತ್ತರ:
ಬ್ಯಾಟ್ನ ಬೆಲೆ x ಆಗಿರಲಿ ಮತ್ತು ಚೆಂಡಿನ ಬೆಲೆ y ಆಗಿರಲಿ
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ ಬೀಜಗಣಿತೀಯವಾಗಿ
3x + 6y = 3900 x + 2y = 1300 ಗೆ
x + 2y = 1300 x = 1300 – 2y
For 3x + 6y = 3900

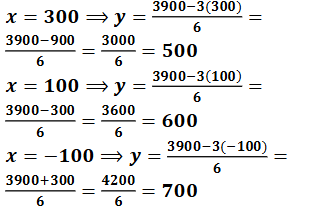
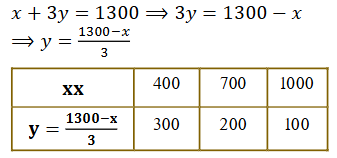
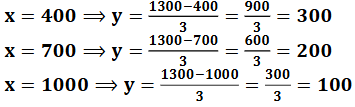
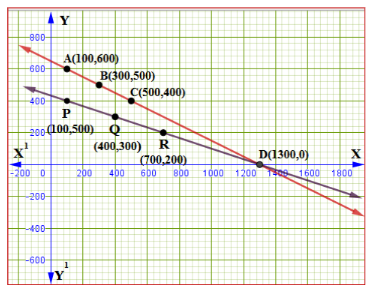
ಎರಡು ಸರಳರೇಖೆಗಳು ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸುತ್ತವೆ. ಹಾಗಾಗಿ ನಿಖರವಾದ ಅನನ್ಯವಾದ ಒಂದು ಪರಿಹಾರವಿದೆ. ಈ ಛೇದನ ಬಂದುವಿನ ನಿರ್ದೇಶಾಂಕಗಳು(1300, 0)
ಬ್ಯಾಟಿನ ಬೆಲೆ = ರೂ 1300, ಚೆಂಡಿನ ಬೆಲೆ = ರೂ 0
3. ಒಂದು ದಿನ 2 kg ಸೇಬು ಮತ್ತು 1 kg ದ್ರಾಕ್ಷಿಯ ಬೆಲೆಯು ₹160 ಆಗಿರುವುದು ಕಂಡುಬಂತು. ಒಂದು ತಿಂಗಳ ಬಳಿಕ 4 kg ಸೇಬು ಮತ್ತು 2 kg ದ್ರಾಕ್ಷಿಗಳ ಬೆಲೆಯು ₹ 300 ಆಗಿತ್ತು. ಈ ಸಂದರ್ಭವನ್ನು ಬೀಜಗಣಿತೀಯವಾಗಿ ಮತ್ತು ರೇಖಾಗಣಿತೀಯವಾಗಿ ಪ್ರತಿನಿಧಿಸಿ.
ಉತ್ತರ:
ಒಂದು ಕೆ.ಜಿ. ಸೇಬಿನ ಬೆಲೆ x ಆಗಿರಲಿ
ಒಂದು ಕೆ.ಜಿ. ದ್ರಾಕ್ಷಿಯ ಬೆಲೆ y ಆಗಿರಲಿ
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ ಬೀಜಗಣಿತೀಯವಾಗಿ
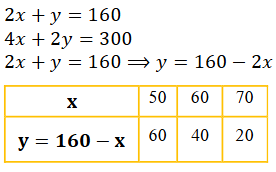
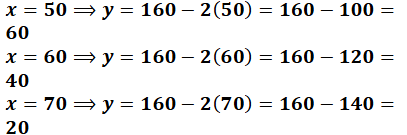
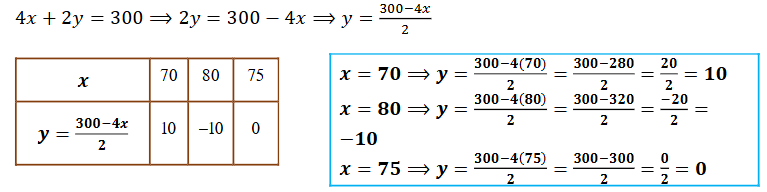
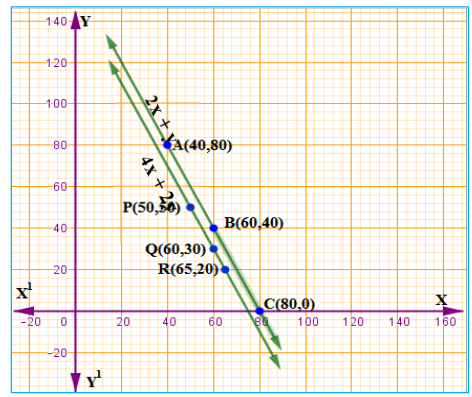
ಎರಡು ಸರಳ ರೇಖೆಗಳು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿದೆ. ಹಾಗಾಗಿ ಈ ಎರಡು ಸಮೀಕರಣಗಳಿಗೆ ಯಾವುದೇ ಪರಿಹಾರವಿರುವುದಿಲ್ಲ.
ಅಭ್ಯಾಸ 3.2
1. ಕೆಳಗೆ ನೀಡಿರುವ ಸಮಸ್ಯೆಗಳಿಗೆ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ರಚಿಸಿರಿ ಮತ್ತು ನಕ್ಷಾಕ್ರಮದಿಂದ ಅವುಗಳಿಗೆ ಪರಿಹಾರಗಳನ್ನು
(i) X ತರಗತಿಯ 10 ವಿದ್ಯಾರ್ಥಿಗಳು ಗಣಿತ ರಸಪ್ರಶ್ನೆಯಲ್ಲಿ ಭಾಗವಹಿಸಿದರು. ಹುಡುಗರ ಸಂಖ್ಯೆಗಿಂತ, ಹುಡುಗಿಯರ ಸಂಖ್ಯೆಯು ಹೆಚ್ಚಾಗಿದ್ದರೆ ರಸಪ್ರಶ್ನೆಯಲ್ಲಿ 4 ಭಾಗವಹಿಸಿದ ಹುಡುಗರ ಮತ್ತು ಹುಡುಗಿಯರ ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಹುಡುಗರ ಸಂಖ್ಯೆಯು x ಆಗಿರಲಿ
ಹುಡುಗಿಯರ ಸಂಖ್ಯೆಯು y ಆಗಿರಲಿ
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ ಬೀಜಗಣಿತೀಯವಾಗಿ
x+y=10
ಹಾಗೂ ಹುಡುಗಿಯರ ಸಂಖ್ಯೆ ಹುಡುಗರ ಸಂಖ್ಯೆ
y=x+4
ಈ ಕೆಳಗಿನಂತೆ ಸರಳಸಮೀಕರಣಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ
x + y = 10 (i)
y=x+4 (ii)
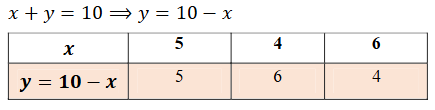
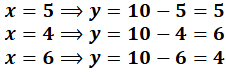
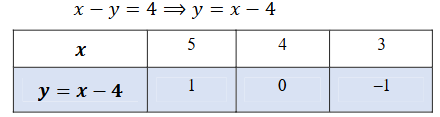
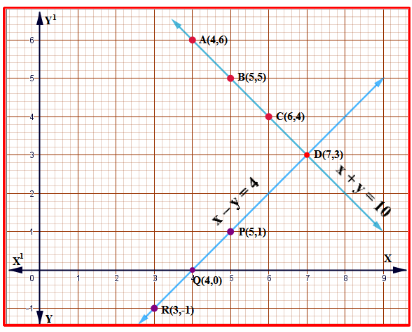
ಎರಡು ಸರಳರೇಖೆಗಳು (7, 3) ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
ಆದ್ದರಿಂದ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ ಅಪೇಕ್ಷಿತ ಪರಿಹಾರ x = 7 y = 3 ಹುಡುಗಿಯರ ಸಂಖ್ಯೆ = 7, ಹುಡುಗರ ಸಂಖ್ಯೆ = 3
ii) 5 ಪೆನ್ಸಿಲು ಮತ್ತು 7 ಪೆನ್ನುಗಳ ಒಟ್ಟು ಬೆಲೆ ₹50. ಹಾಗೆಯೇ 7 ಪೆನ್ಸಿಲು ಮತ್ತು 5 ಪೆನ್ನುಗಳ ಒಟ್ಟು ಬೆಲೆ ₹46. ಪ್ರತಿಯೊಂದು ಪೆನ್ಸಿಲಿನ ಹಾಗೂ ಪೆನ್ನಿನ ಬೆಲೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಒಂದು ಪೆನ್ಸಿಲಿನ ಬೆಲೆ x ಆಗಿರಲಿ
ಒಂದು ಪೆನ್ನಿನ ಬೆಲೆ y ಆಗಿರಲಿ
5 ಪೆನ್ಸಿಲ್ ಮತ್ತು 7 ಪೆನ್ನಿನ ಬೆಲೆ = ₹ 50
5x + 7y = 50 (i)
7 ಪೆನ್ಸಿಲ್ ಮತ್ತು 5 ಪೆನ್ನಿನ ಬೆಲೆ = ₹ 46
7x + 5y = 46 (ii)
5x + 7y = 50 ಆದಾಗ
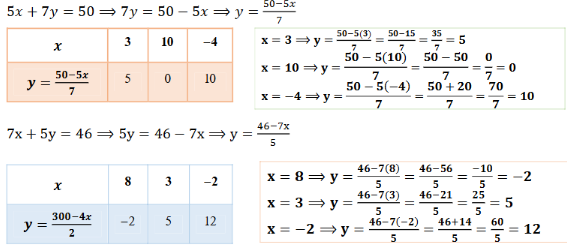
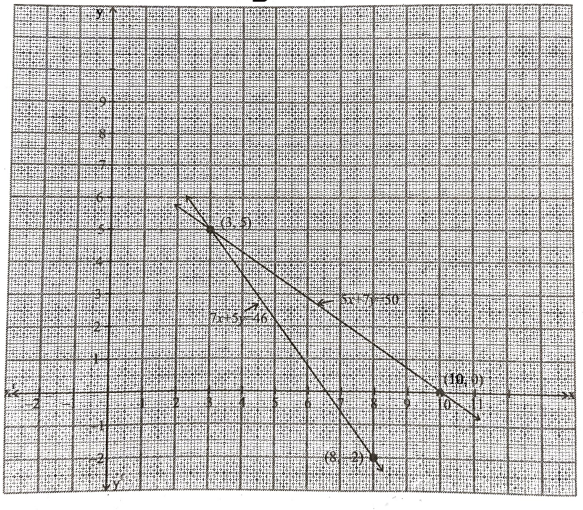
ಎರಡು ಸರಳರೇಖೆಗಳು (3, 5) ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
ಆದ್ದರಿಂದ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ ಅಪೇಕ್ಷಿತ ಪರಿಹಾರ
x = 3, y = 5
ಪೆನ್ಸಿಲ್ನ ಬೆಲೆ = ರೂ 3
ಪೆನ್ನಿನ ಬೆಲೆ = ರೂ 5
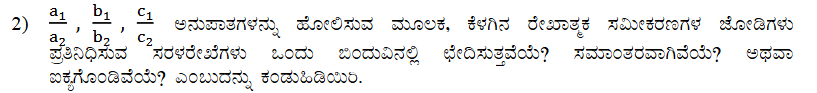
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
ಉತ್ತರ:
5x – 4y + 8 = 0 (i)
7x + 6y – 9 = 0 (ii)
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 5 b1 = -4 c1 = 8
a2 = 7 b2 = 6 c2 = -9
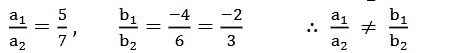
ಆದ್ದರಿಂದ (i) ಮತ್ತು (ii) ಛೇದಿಸುವ ರೇಖೆಗಳು
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
ಉತ್ತರ:
ಉ. ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣ ಜೋಡಿಗಳು
9x + 3y + 12 = 0
18x + 6y + 24 = 0
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 9 b1 = 3 c1 = 12
a2 = 18 b2 = 6 c2 = 24
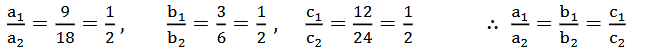
ಎರಡು ರೇಖೆಗಳು ಪರಸ್ಪರ ಐಕ್ಯಗೊಳ್ಳುತ್ತದೆ.
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣ ಜೋಡಿಗಳು
6x – 3y + 10 = 0
2x – y + 9 = 0
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 6 b1 = -3 c1 = 10
a2 = 2 b2 = -1 c2 = 9
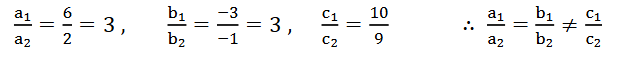
ಎರಡು ರೇಖೆಗಳು ಸಮಾಂತರವಾಗಿವೆ.
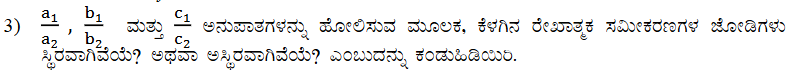
(1) 3x + 2y = 5; 2x – 3y = 7
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
3x + 2y – 5 = 0 (1)
2x – 3y – 7 = 0 (2)
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 3 b1 = 2 c1 = -5
a2 = 2 b2 = -3 c2 = -9
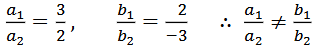
ಎರಡು ರೇಖೆಗಳು ಛೇದಿಸುತ್ತವೆ.
(ii) 2x – 3y = 8; 4x – 6y = 9
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
2x – 3y – 8 = 10 (1)
4x – 6y – 9 = 0 (2)
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 2 b1 = -3 c1 = -8
a2 = 4 b2 = -6 c2 = -9
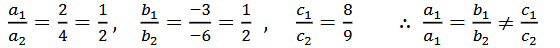
ಎರಡು ರೇಖೆಗಳು ಸಮಾಂತರವಾಗಿವೆ.
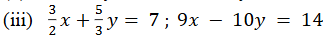
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
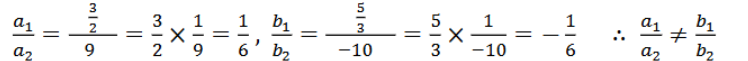
ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು ಛೇದಿಸುತ್ತದೆ.
(iv) 5x – 3y = 11; – 10x + 6y = – 22
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
5x – 3y – 11 = 0
-10x + 6y + 22 = 0
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 5 b1 = -3 c1 = -11
a2 = -10 b2 = 6 c2 = 22
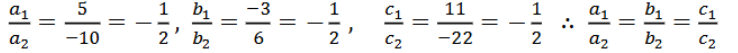
ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು ಪರಸ್ಪರ ಐಕ್ಯಗೊಳ್ಳುತ್ತವೆ.
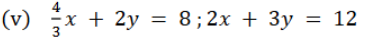
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
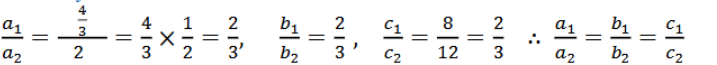
ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳು ಪರಸ್ಪರ ಐಕ್ಯಗೊಳ್ಳುತ್ತವೆ.
4. ಮುಂದೆ ನೀಡಿದವುಗಳಲ್ಲಿ ಯಾವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳು ಸ್ಥಿರವಾಗಿವೆ/ಅಸ್ಥಿರವಾಗಿವೆ? ಸ್ಥಿರವಾಗಿದ್ದರೆ, ನಕ್ಷಾಕ್ರಮದಿಂದ ಪರಿಹಾರವನ್ನು ಪಡೆಯಿರಿ.
(i) x + y = 5; 2x + 2y = 10
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
x + y – 5 = 0 (1)
2x + 2y – 10 = 0 (2)
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 1 b1 = 1 c1 = -5
a2 = 2 b2 = 2 c2 = -10

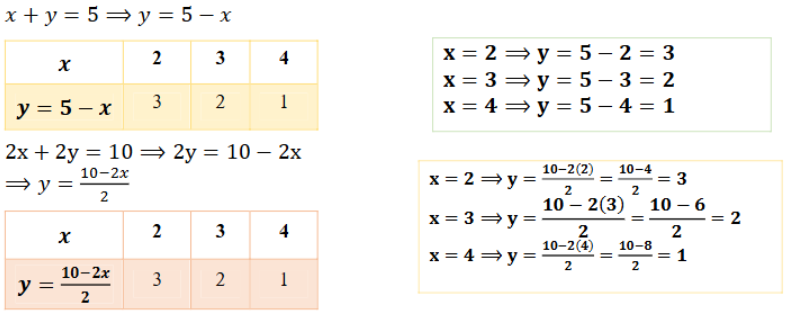
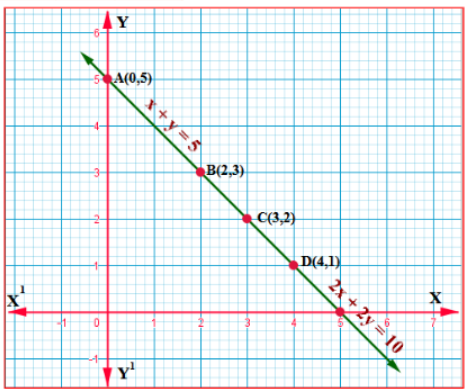
(ii) x – y = 8; 3x – 3y = 16
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ

(iii) 2r + y – 6 = 0; 4x – 2y – 4 = 0
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವನ್ನು ಈ ಕೆಳಕಂಡಂತೆ ಬರೆದಾಗ
2x + y – 6 = 0 … (1)
4x – 2y – 4 = 0 …(2)
ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನು ಪರಿಶೀಲಿಸಿ ಅವುಗಳ ಬೆಲೆಗಳನ್ನು ಹೋಲಿಸಿ ನೋಡಿದಾಗ
a1 = 2 b1 = 1 c1 = -6
a2 = 4 b2 = -2 c2 = -4
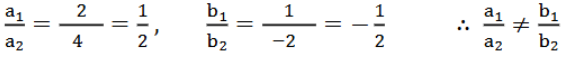
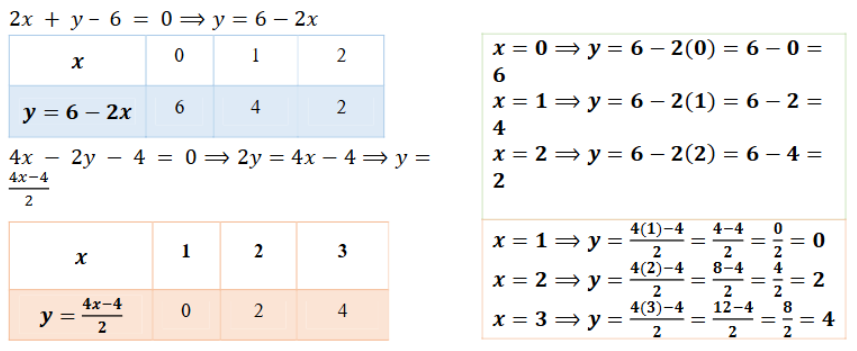
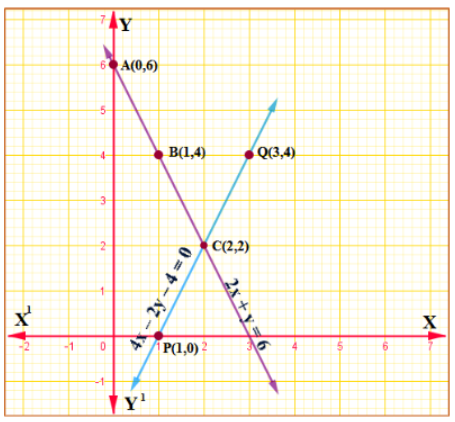
AB ಮತ್ತು DE ರೇಖೆಗಳು C(2,2) ನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ. .. x = 2 y = 2
(iv) 2x – 2y – 2 = 0; 4x – 4y – 5 = 0
ಉತ್ತರ:
2x – 2y – 2 = 0 … (1)
4x – 4y – 5 = 0 (2)
a1 = 2 b1 = -2 c1 = -2
a2 = 4 b2 = -4 c2 = -5
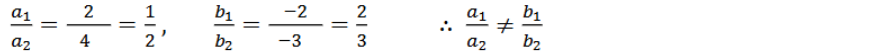
ಸಮೀಕರಣದ ಜೋಡಿಗಳು ಅಸ್ಥಿರವಾಗಿವೆ
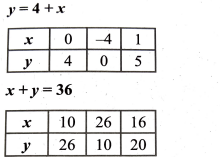
5. ಉದ್ದವು ಅಗಲಕ್ಕಿಂತ 4m ಹೆಚ್ಚಾಗಿರುವ ಆಯತಾಕಾರದ ಒಂದು ಹೂದೋಟದ ಸುತ್ತಳತೆಯ ಅರ್ಧವು 36m. ಹೂದೋಟದ ಅಳತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಆಯತಾಕಾರದ ಹೂದೋಟದ ಅಗಲವು = x ಆಗಿರಲಿ
ಹೂದೋಟದ ಉದ್ದವು = ym ಆಗಿರಲಿ
ಕೊಟ್ಟಿರುವ ಹೇಳಿಕೆಯಂತೆ
ಉದ್ದ = 4 + x
4 + x = y
y – x = 4 ಹೂದೋಟದ ಸುತ್ತಳತೆಯು ಅರ್ಧ = 36
y + x = 36
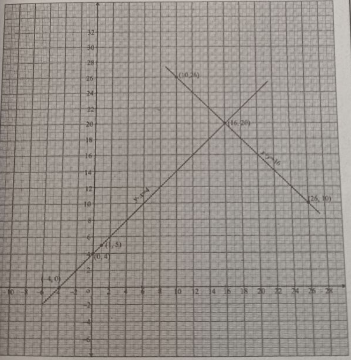
6. ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ 2x + 3y – 8 = 0 ಯನ್ನು ನೀಡಲಾಗಿದೆ. ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳನ್ನು ಬರೆಯಿರಿ, ಹೇಗೆಂದರೆ ಉಂಟಾದಂತಹ ಜೋಡಿಗಳ ರೇಖಾಗಣಿತೀಯ ಪ್ರತಿನಿಧಿಸುವಿಕೆಯು ಈ ಕೆಳಗಿನಂತಿರಬೇಕು.
(i) ಛೇದಿಸುವ ರೇಖೆಗಳು (ii) ಸಮಾಂತರ ರೇಖೆಗಳು
(iii) ಐಕ್ಯಗೊಳ್ಳುವ ರೇಖೆಗಳು
ಉತ್ತರ:
(i) ಛೇದಿಸುವ ರೇಖೆಗಳು ಸಮೀಕರಣದ ಜೋಡಿಯು 2x + 3y – 8 = 0
ಇಲ್ಲಿ a1 = 2 b1 = 3 c1 = – 8
a2x + b2y + c2= 0
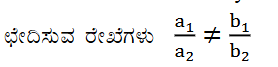
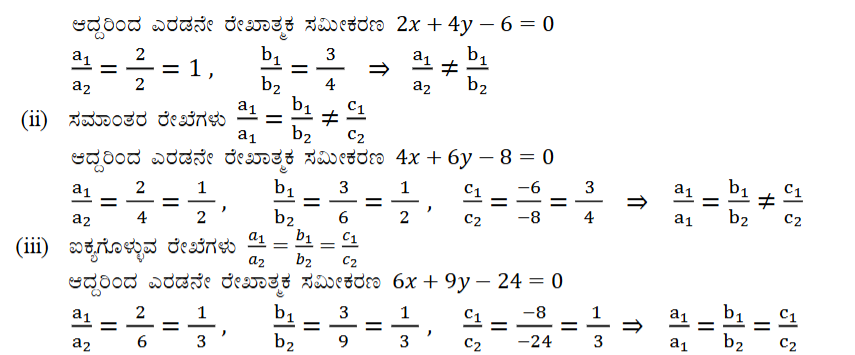
2x + 3y – 8 = 0 ರೇಖೆಗೆ ಸಮಾಂತರವಾಗಿ 2(2x + 3y – 8); 4x + 6y – 16 = 0 ತೆಗೆದುಕೊಳ್ಳಬಹುದು.
7. x – y + 1 = 0 ಮತ್ತು 3x + 2y – 12 = 0 ಸಮೀಕರಣಗಳ ನಕ್ಷೆಗಳನ್ನು ಎಳೆಯಿರಿ. ಈ ರೇಖೆಗಳು ಮತ್ತು x – ಅಕ್ಷದಿಂದ ಉಂಟಾಗುವ ತ್ರಿಭುಜದ ಶೃಂಗಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ನಿರ್ಧರಿಸಿರಿ ಹಾಗೂ ತ್ರಿಕೋನೀಯ ವಲಯವನ್ನು ಛಾಯೆಗೊಳಿಸಿರಿ.
ಉತ್ತರ:
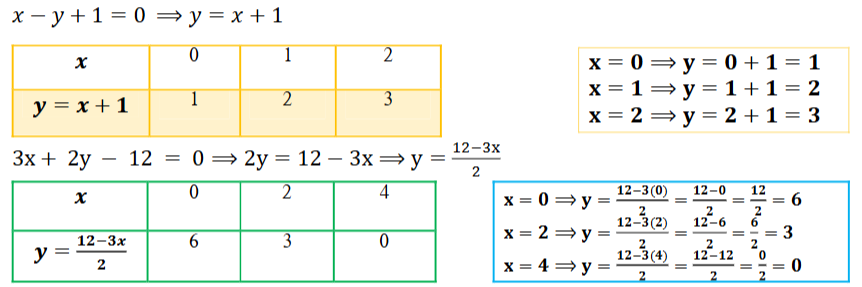
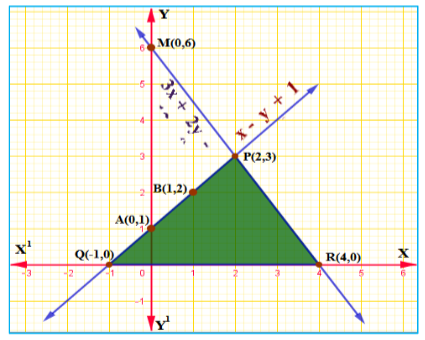
ಛಾಯೆಗೊಳಿಸಿದ ತ್ರಿಕೋನಿಯ ವಲಯದ ಶೃಂಗಬಿಂದುಗಳು (4,0) (-1, 0) (2,3)
ಅಭ್ಯಾಸ 3.3
1. ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ಆದೇಶ ವಿಧಾನದಿಂದ ಬಿಡಿಸಿ.
(1) x + y = 14; x – y =4
ಉತ್ತರ:
x + y = 14 (1)
x – y = 4
y = x – 4 (2)
ಸಮೀಕರಣ 2ನ್ನು 1ರಲ್ಲಿ ಸೇರಿಸಿದಾಗ
x + x – 4 = 14
2x = 18
x = 9
x =9 ನ್ನು ಸಮೀಕರಣ 2ರಲ್ಲಿ ಸೇರಿಸಿದಾಗ
y = 9 – 4
y = 5
x = 9, y = 5
(ii) s – t = 3
ಉತ್ತರ:

(iii) 3x – y = 3 ಮತ್ತು 9x – 3y = 9
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣದ ಜೋಡಿಗಳು
3x – y = 3
y = 3x – 3
ಮತ್ತು 9x – 3y = 9 (2)
y = 3x – 3 ನ್ನು ಸಮೀಕರಣ 2ರಲ್ಲಿ ಸೇರಿಸಿದಾಗ
9x – 3(3x – 3) =9 → 9x – 9x + 9 = 9 → 9 = 9
ಆದ್ದರಿಂದ x ನ ಎಲ್ಲಾ ಬೆಲೆಗಳಿಗೂ ಈ ಹೇಳಿಕೆ ನಿಜವಾಗಿದೆ. ಹಾಗಿದ್ದರೂ x ಗೆ ಒಂದು ನಿರ್ಧಿಷ್ಟವಾದ ಬೆಲೆ ಪರಿಹಾರವಾಗಿ ಸಿಗುವುದಿಲ್ಲ.
(iv) 0.2x + 0.3y = 1.3 and 0.4x + 0.5y = 2.3
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣದ ಜೋಡಿಗಳು
0.2x + 0.3y = 1.3 …… (1)
0.4x + 0.5y = 2.3 ….. (2)
ಎರಡು ಸಮೀಕರಣಗಳನ್ನು 10ರಿಂದ ಗುಣಿಸಿದಾಗ
2x + 3y = 13 ……(3)
4x + 5y = 23 …… (4)
2x + 3y = 13 ತೆಗೆದುಕೊಂಡಾಗ 2x = 13 – 3y
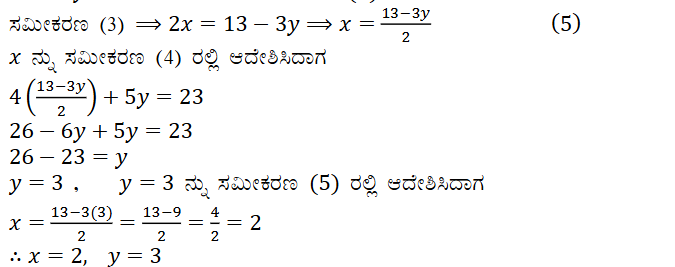
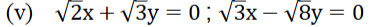
ಉತ್ತರ:
ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣದ ಜೋಡಿಗಳು
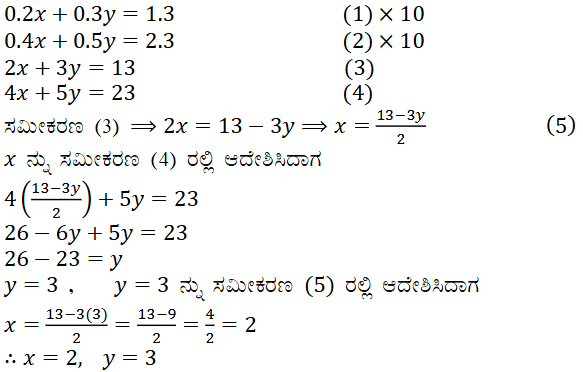
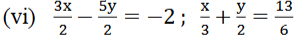
ಉತ್ತರ:
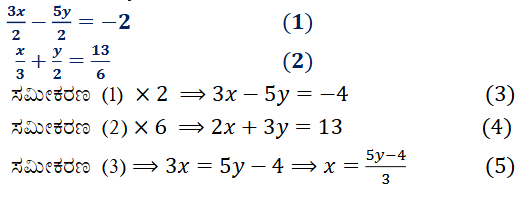
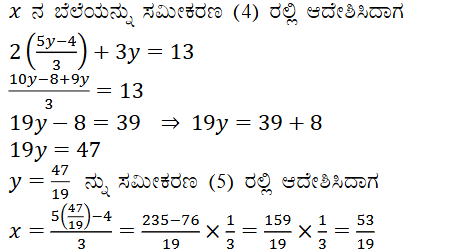
2. 2x + 3y = 11 ಮತ್ತು 2x – 4y = – 24 ಬಿಡಿಸಿರಿ ಮತ್ತು ಇದರಿಂದ y = mx + 3 ರಲ್ಲಿ m’ ನ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
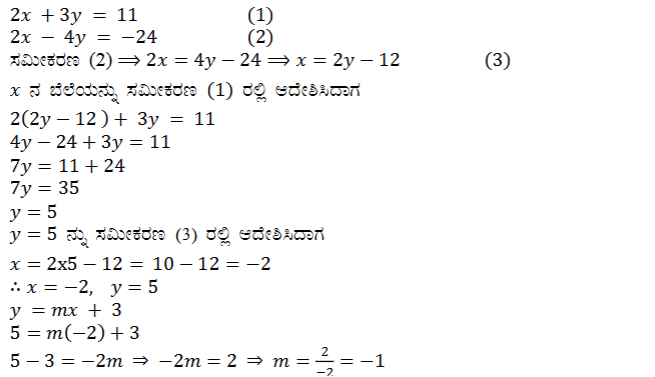
3. ಕೆಳಗಿನ ಸಮಸ್ಯೆಗಳಿಗೆ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ರಚಿಸಿರಿ ಮತ್ತು ವಿಧಾನದಿಂದ ಅವುಗಳ ಕಂಡುಹಿಡಿಯಿರಿ. ಆದೇಶ ಪರಿಹಾರಗಳನ್ನು
(i) ಎರಡು ಸಂಖ್ಯೆಗಳ ವ್ಯತ್ಯಾಸ 26 ಮತ್ತು ಒಂದು ಸಂಖ್ಯೆಯು ಇನ್ನೊಂದರ ಮೂರರಷ್ಟಿದೆ ಅವುಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಸಂಖ್ಯೆಗಳು x ಮತ್ತು y ಆಗಿರಲಿ
ಎರಡು ಸಂಖ್ಯೆಗಳ ವ್ಯತ್ಯಾಸ 26
i.e., x – y = 26 (1)
ಒಂದು ಸಂಖ್ಯೆಯು ಮತ್ತೊಂದು ಸಂಖ್ಯೆಯ 3ರಷ್ಟು ಇದ್ದರೆ
i.e., x = 3y (2)
x =3y ನ್ನು ಸಮೀಕರಣ (1)ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ
3y – y = 26
2y =26 → y=13
y=13ನ್ನು ಸಮೀಕರಣ (2)ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ
x=3×13 → x = 39
x = 39 2 y = 13
(ii) ಎರಡು ಪರಿಪೂರಕ ಕೋನಗಳಲ್ಲಿ ದೊಡ್ಡ ಕೋನವು ಚಿಕ್ಕ ಕೋನಕ್ಕಿಂತ 18 ಡಿಗ್ರಿ ಅಧಿಕವಾಗಿದೆ. ಅವುಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:


(iii) ಕ್ರಿಕೆಟ್ ತಂಡವೊಂದರ ತರಬೇತುಗಾರ್ತಿಯು 1 ಬ್ಯಾಟ್ಗಳು ಮತ್ತು 6 ಚೆಂಡುಗಳನ್ನು ₹ 3800 ಕ್ಕೆ ಕೊಳ್ಳುತ್ತಾರೆ. ಆ ಬಳಿಕ 3 ಬ್ಯಾಟ್ ಗಳು ಮತ್ತು 5 ಚೆಂಡುಗಳನ್ನು ಅವರು ₹ 1750 ಕ್ಕೆ ಕೊಳ್ಳುತ್ತಾರೆ. ಪ್ರತಿಯೊಂದು ಬ್ಯಾಟ್ ಮತ್ತು ಪ್ರತಿಯೊಂದು ಚೆಂಡಿನ ಬೆಲೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಬ್ಯಾಟ್ನ ಬೆಲೆ x ಆಗಿರಲಿ
ಚೆಂಡಿನ ಬೆಲೆ y ಆಗಿರಲಿ

(iv) ಒಂದು ನಗರದಲ್ಲಿ ಟ್ಯಾಕ್ಸಿ ಬಾಡಿಗೆಯು ಎರಡು ಭಾಗಗಳಿಂದ ಕೂಡಿದೆ. ಮೊದಲನೆಯದು ನಿಗದಿತ ಬಾಡಿಗೆ ಮತ್ತು ಎರಡನೆಯದು ಚಲಿಸಿದ ದೂರಕ್ಕೆ ಅನುಗುಣವಾಗಿ ಬಾಡಿಗೆ. ಇವೆರಡನ್ನು ಸೇರಿಸಿ ಒಟ್ಟು ಬಾಡಿಗೆ ಎನ್ನುತ್ತೇವೆ. ಒಟ್ಟು ಬಾಡಿಗೆಯು 10km ಪ್ರಯಾಣಕ್ಕೆ ₹105 ಮತ್ತು 15km ಪ್ರಯಾಣಕ್ಕೆ ₹155. ಹಾಗಾದರೆ ನಿಗದಿತ ಬಾಡಿಗೆ ಮತ್ತು ಪ್ರತಿ ಕಿಲೋಮೀಟರ್ನ ಪ್ರಯಾಣಕ್ಕೆ ಬಾಡಿಗೆ ದರಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ. ಒಬ್ಬ ವ್ಯಕ್ತಿಯು 25km ದೂರವನ್ನು ಪ್ರಯಾಣಿಸಿದರೆ ನೀಡಬೇಕಾದ ಒಟ್ಟು ಬಾಡಿಗೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

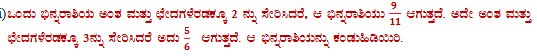
ಉತ್ತರ:
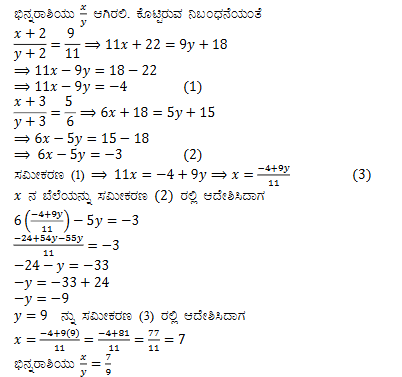
(vi) ಐದು ವರ್ಷಗಳ ಬಳಿಕ ಜೇಕಬ್ ರ ವಯಸ್ಸು ಅವರ ಮಗನ ವಯಸ್ಸಿನ ಮೂರರಷ್ಟಾಗುತ್ತದೆ. ಐದು ವರ್ಷಗಳ ಹಿಂದೆ ಜೇಕಬ್ ರ ವಯಸ್ಸು ಅವರ ಮಗನ ವಯಸ್ಸಿನ ಏಳರಷ್ಟಿತ್ತು ಅವರಿಬ್ಬರ ಈಗಿನ ವಯಸ್ಸು ಎಷ್ಟು?
ಉತ್ತರ:
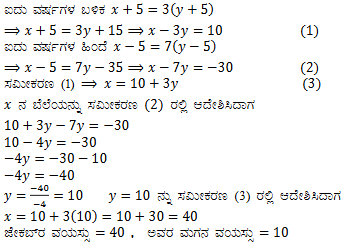
ಅಭ್ಯಾಸ 3.2
1. ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ವರ್ಜಿಸುವ ವಿಧಾನ ಮತ್ತು ಆದೇಶ ವಿಧಾನಗಳಿಂದ ಬಿಡಿಸಿರಿ.
(i) x + y = 5 ಮತ್ತು 2x – 3y = 4
ಉತ್ತರ:


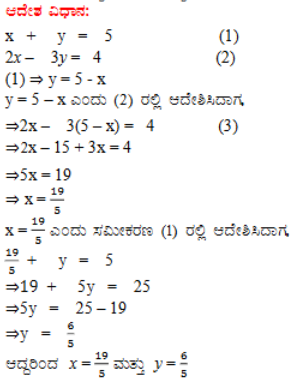
(ii) 3x + 4y = 10 ಮತ್ತು 2x – 2y = 2
ಉತ್ತರ:

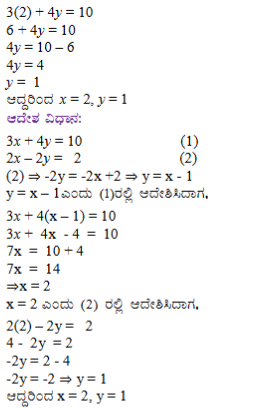
(iii) 3x – 5y – 4 = 0 ಮತ್ತು 9x = 2y + 7
ಉತ್ತರ:

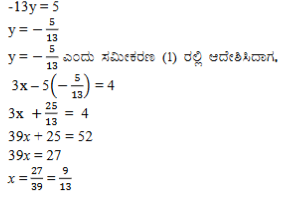
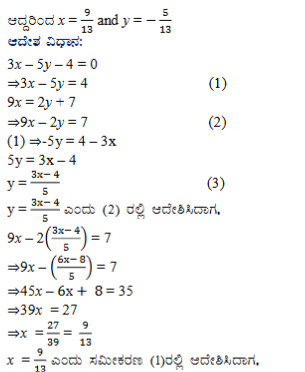
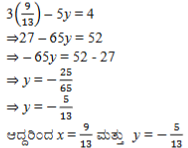
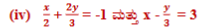
ಉತ್ತರ:
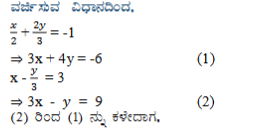

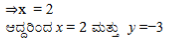

ಕೆಳಗಿನ ಸಮಸ್ಯೆಗಳಿಗೆ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ರಚಿಸಿರಿ ಮತ್ತು ವರ್ಜಿಸುವ ವಿಧಾನದಿಂದ ಅವುಗಳಿಗೆ ಪರಿಹಾರಗಳನ್ನು( ಇರುವುದಾದರೆ) ಕಂಡುಹಿಡಿಯಿರಿ.
(i) ಒಂದು ಭಿನ್ನರಾಶಿಯ ಅಂಶಕ್ಕೆ Iನ್ನು ಸೇರಿಸಿ, ಛೇದದಿಂದ 1ನ್ನು ಕಳೆದು ಸಂಕ್ಷೇಪಿಸಿದರೆ, 1 ಸಿಗುತ್ತದೆ. ಆ ಭಿನ್ನರಾಶಿಯ ಛೇದಕ್ಕೆ 1ನ್ನು ಸೇರಿಸಿದರೆ ಅದು 1/2 ಎಂದಾಗುತ್ತದೆ. ಆ ಭಿನ್ನರಾಶಿ ಯಾವುದು?
ಉತ್ತರ:
ಅಂಶವು x ಆಗಿರಲಿ ಮತ್ತು ಛೇದವು y ಆಗಿರಲಿ
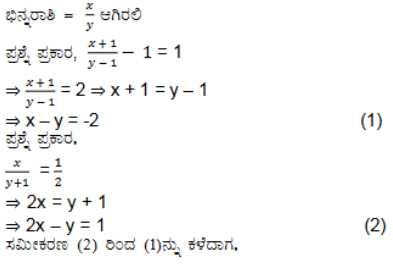

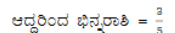
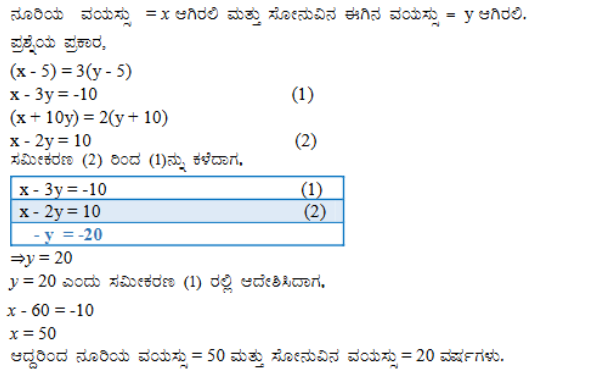
(ii) ಐದು ವರ್ಷಗಳ ಹಿಂದೆ ನೂರಿಯ ವಯಸ್ಸು ಸೋನುವಿನ ವಯಸ್ಸಿನ ಮೂರು ಪಟ್ಟು ಆಗಿತ್ತು. ಹತ್ತು ವರ್ಷಗಳ ಬಳಿಕ ನೂರಿಯ ವಯಸ್ಸು ಸೋನುವಿನ ವಯಸ್ಸಿನ ಎರಡು ಪಟ್ಟು ಆಗುತ್ತದೆ. ಹಾಗಾದರೆ, ನೂರಿ ಮತ್ತು ಸೋನುವಿನ ಈಗಿನ ವಯಸ್ಸೆಷ್ಟು?
ಉತ್ತರ:
(iii) ಎರಡಂಕೆಯ ಒಂದು ಸಂಖ್ಯೆಯ ಅಂಕೆಗಳ ಮೊತ್ತ 9. ಇದರಲ್ಲಿರುವ ಅಂಕೆಗಳ ಕ್ರಮವನ್ನು ಅದಲು ಬದಲು ಮಾಡಿದಾಗ ಸಿಗುವ ಸಂಖ್ಯೆಯನ್ನು ಇಮ್ಮಡಿಗೊಳಿಸಿದರೆ, ಅದು ಮೊದಲನೇ ಸಂಖ್ಯೆಯ ಒಂಭತ್ತರಷ್ಟಕ್ಕೆ ಸಮವಾಗುತ್ತದೆ. ಆ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

iv) ₹2000 ವನ್ನು ಹಿಂಪಡೆಯಲು ಮೀನಾ ಬ್ಯಾಂಕಿಗೆ ಹೊದಳು. ಅವಳು ನಗದು ಗುಮಾಸ್ತರಲ್ಲಿ ₹50 ರ ಮತ್ತು ₹100 ರ ನೋಟುಗಳನ್ನು ಮಾತ್ರ ನೀಡುವಂತೆ ಹೇಳಿದಳು. ಮೀನಾಳಿಗೆ ಒಟ್ಟು 25 ನೋಟುಗಳು ದೊರೆತವು. ₹50 ರ ಮತ್ತು ₹100 ರ ಎಷ್ಟೆಷ್ಟು ನೋಟುಗಳನ್ನು ಅವಳು ಪಡೆದಳು ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
₹50 ನೋಟಿನ ಸಂಖ್ಯೆಯು x ಆಗಿರಲಿ
₹100 ನೋಟಿನ ಸಂಖ್ಯೆಯು y ಆಗಿರಲಿ
ಮೊದಲಿನ ಹೇಳಿಕೆಯಂತೆ
50x + 100y = 2000
x + 2y = 40 ….(1)
ಎರಡನೇಯ ಹೇಳಿಕೆಯಂತೆ
x – y = 25 …..(2)
ಸಮೀಕರಣ 2ನ್ನು 1ರಿಂದ ಕಳೆದಾಗ

(v) ಒಂದು ಎರವಲು ಗ್ರಂಥಾಲಯದಲ್ಲಿ ಮೊದಲ ಮೂರು ದಿನಕ್ಕೆ ಒಂದು ನಿಗದಿತ ಶುಲ್ಕವಿರುತ್ತದೆ. ಆ ಬಳಿಕದ ಪ್ರತಿಯೊಂದು ದಿನಕ್ಕೂ ಹೆಚ್ಚುವರಿ ಶುಲ್ಕವಿರುತ್ತದೆ. ಪುಸ್ತಕವನ್ನು ಏಳುದಿನ ತನ್ನಲ್ಲಿ ಇರಿಸಿಕೊಂಡದ್ದಕ್ಕಾಗಿ ಸರಿತಾ ₹27 ನ್ನು ಪಾವತಿಸಿದರೆ, ಪುಸ್ತಕವನ್ನು 5 ದಿನ 88 ಘಟಕ 3 ಇರಿಸಿಕೊಂಡದ್ದಕ್ಕಾಗಿ ಸೂಸಿ ₹ 21 ನ್ನು ಪಾವತಿಸಿದಳು, ನಿಗದಿತ ಶುಲ್ಕ ಮತ್ತು ಪ್ರತಿಯೊಂದು ಹೆಚ್ಚುವರಿ ದಿನದ ಶುಲ್ಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಮೊದಲ ಮೂರು ದಿನಕ್ಕೆ ನಿಗದಿತ ಶುಲ್ಕ x
ಹೆಚ್ಚುವರಿ ಶುಲ್ಕವು y ಆಗಿರಲಿ.
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ
7 ದಿನಗಳಿಗೆ ಸರಿತ ಪಾವತಿಸಿದ ಹಣ = 27
x + 4(y) = 27
x + 4y = 27 -(1)
5 ದಿನಗಳಿಗೆ ಸೂಸಿ ಪಾವತಿಸಿದ ಹಣ = 21
x + 2y = 21
ಸಮೀಕರಣ Iನ್ನು 2ರಿಂದ ಕಳೆದಾಗ
2y =27- 21→ 2y = 6 → y = 3
y = 3 ಸಮೀಕರಣ 1ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ
x + 4(3) = 27
x + 12 = 27
x = 27 – 12
x = 15
ಮೊದಲ ಮೂರು ದಿನಕ್ಕೆ ನಿಗದಿತ ಶುಲ್ಕ ₹15 ಪ್ರತಿದಿನಕ್ಕೂ ಹೆಚ್ಚುವರಿ ಶುಲ್ಕವು ₹3.
ಅಭ್ಯಾಸ 3.5
1. ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳಲ್ಲಿ ಯಾವುದಕ್ಕೆ ಅನನ್ಯ ಪರಿಹಾರ ಅಥವಾ ಅಪರಿಮಿತ ಸಂಖ್ಯೆಯ ಪರಿಹಾರಗಳಿರುತ್ತವೆ? ಯಾವುದಕ್ಕೆ ಪರಿಹಾರವಿರುವುದಿಲ್ಲ? ಅನನ್ಯ ಪರಿಹಾರ ಇರುವುದಾದರೆ ಓರೆ ಗುಣಾಕಾರ ವಿಧಾನದಿಂದ ಅದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) x – 3y – 3 = 0 ಮತ್ತು 3x – 9y – 2 = 0
ಉತ್ತರ:
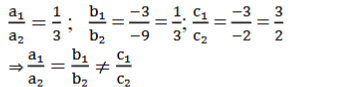
ಆದ್ದರಿಂದ ದತ್ತ ಸಮೀಕರಣ ರೇಖಾತ್ಮಕ ಜೋಡಿಯು ಪರಸ್ಪರ ಸಮಾಂತರವಾಗಿದೆ. ಅವುಗಳು ಪರಸ್ಪರ ಛೇದಿಸುವುದಿಲ್ಲ ಆದ್ದದಿಂದ ಅವುಗಳಿಗೆ ಯಾವುದೇ ಪರಿಹಾರವಿರುವುದಿಲ್ಲ.
(ii) 2x + y=5 ಮತ್ತು 3x + 2y = 8
ಉತ್ತರ:
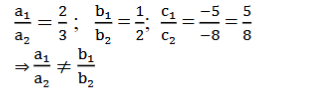
ಆದ್ದರಿಂದ ದತ್ತ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳಿಗೆ ಅನನ್ಯ ಪರಿಹಾರವಿದೆ.
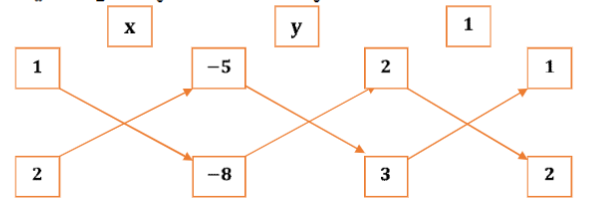
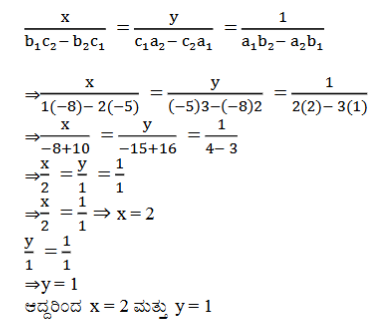
iii) 3x – 5y = 20 ಮತ್ತು 6x – 10y = 40
ಉತ್ತರ:
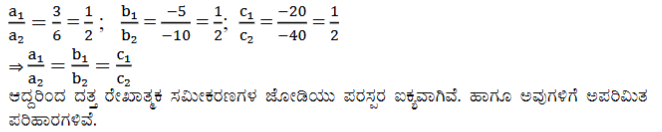
(iv) x-3y-7=0 ಮತ್ತು 3x-3y-15 = 0
ಉತ್ತರ:
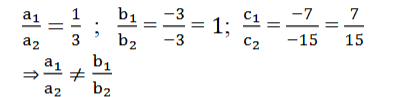
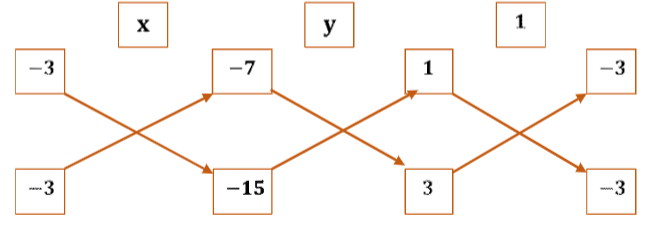
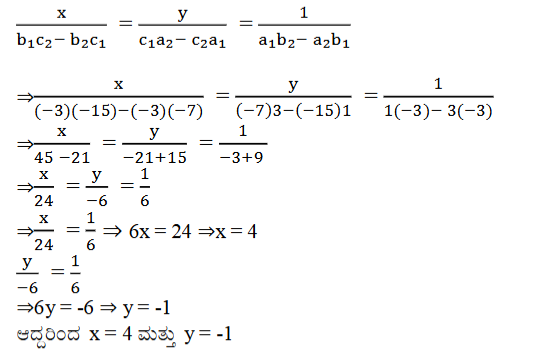
2. i) a ಮತ್ತು b ಗಳ ಯಾವ ಬೆಲೆಗಳಿಗೆ ಕೆಳಗೆ ನೀಡಿದ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಯು ಅಪರಿಮಿತ ಸಂಖ್ಯೆಯ ಪರಿಹಾರಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ?
2x + 3y = 7
(a – b)x + (a + b)y = 3a + b – 2
ಉತ್ತರ:
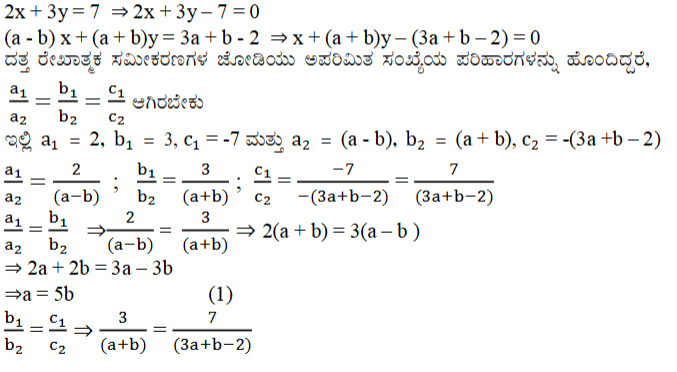
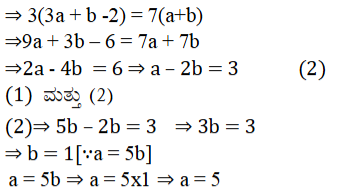
a = 5 ಮತ್ತು b = 1
ii) k ಯ ಯಾವ ಬೆಲೆಗೆ ಕೆಳಗೆ ನೀಡಿದ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಯು ಯಾವುದೇ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ?
3x + y = 1
(2k – 1)x + (k – 1) y = 2k + 1
ಉತ್ತರ:
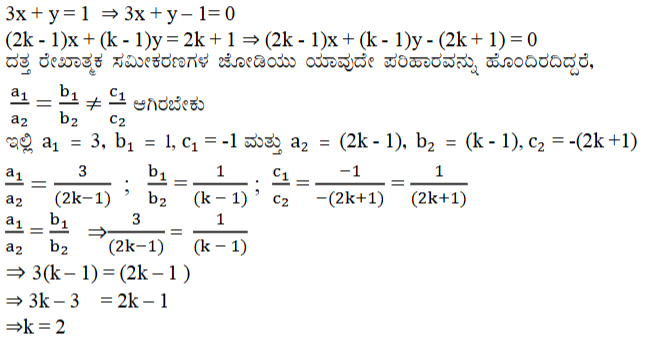
k = 2 ಕೊಟ್ಟಿರುವ ಸಮೀಕರಣವು ಯಾವುದೇ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ.
3. ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಯನ್ನು ಆದೇಶ ವಿಧಾನ ಮತ್ತು ಓರೆ ಗುಣಾಕಾರ ವಿಧಾನಗಳಿಂದ
8x + 5y = 9
3x + 2y = 4
ಉತ್ತರ:

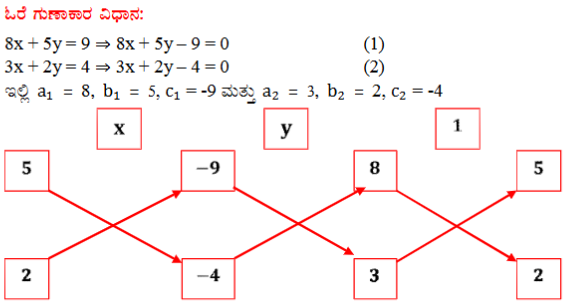
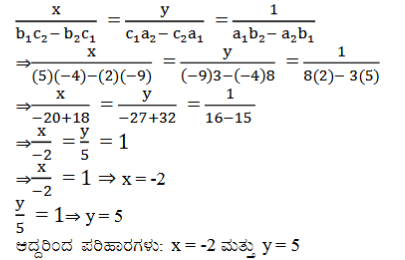
4. ಕೆಳಗೆ ನೀಡಲಾದ ಸಮಸ್ಯೆಗಳಿಗೆ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಯನ್ನು ರಚಿಸಿರಿ ಮತ್ತು ಯಾವುದಾದರೊಂದು ಬೀಜಗಣಿತೀಯ ವಿಧಾನದಿಂದ ಅವುಗಳ ಪರಿಹಾರಗಳನ್ನು (ಇದ್ದರೆ) ಕಂಡುಹಿಡಿಯಿರಿ.
i) ಒಂದು ವಸತಿನಿಲಯದಲ್ಲಿ ಒಟ್ಟು ಶುಲ್ಕವು ಎರಡು ಭಾಗಗಳನ್ನು ಹೊಂದಿದೆ. ಮೊದಲ ಭಾಗವು ನಿಗದಿತ ಶುಲ್ಕ. ಎರಡನೇ ಭಾಗವು ಒಂದು ತಿಂಗಳಲ್ಲಿ ಅವರು ಭೋಜನಶಾಲೆಯಿಂದ ಆಹಾರವನ್ನು ಪಡೆದ ದಿನಗಳಿಗೆ ಅನುಸಾರವಾದ ಶುಲ್ಕ. A ಎಂಬ ವಿದ್ಯಾರ್ಥಿನಿ 20 ದಿನ ಆಹಾರವನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದರಿಂದ, ಅವಳು ₹1000 ವನ್ನು ವಸತಿ ನಿಲಯಕ್ಕೆ ಶುಲ್ಕವಾಗಿ ಪಾವತಿಸಬೇಕಾಯಿತು. B ಎಂಬ ಮತ್ತೊಬ್ಬ ವಿದ್ಯಾರ್ಥಿನಿ 26 ದಿನ ಆಹಾರವನ್ನು ಪಡೆದುಕೊಂಡು ₹1180 ನ್ನು ವಸತಿ ನಿಲಯಕ್ಕೆ ಶುಲ್ಕವಾಗಿ ಪಾವತಿಸಬೇಕಾಯಿತು. ನಿಗದಿತ ಶುಲ್ಕ ಮತ್ತು ಒಂದು ದಿನದ ಆಹಾರದ ಶುಲ್ಕವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಆಹಾರದ ನಿಗದಿತ ಶುಲ್ಕ x ಆಗಿರಲಿ ಮತ್ತು ಪ್ರತಿದಿನ ಆಹಾರದ ಶುಲ್ಕ y ಆಗಿರಲಿ


ii) ಒಂದು ಭಿನ್ನರಾಶಿಯ ಅಂಶದಿಂದ 1ನ್ನು ಕಳೆದಾಗ ಅದು 1/3 ಆಗುತ್ತದೆ ಮತ್ತು ಆ ಭಿನ್ನರಾಶಿಯ ಛೇದಕ್ಕೆ 8ನ್ನು ಸೇರಿಸಿದಾಗ ಅದು 1/4 ಆಗುತ್ತದೆ. ಹಾಗಾದರೆ ಆ ಭಿನ್ನರಾಶಿಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

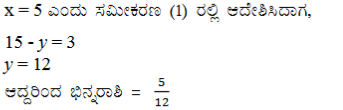
iii) ಯಶ್ ಎಂಬಾತನು ಒಂದು ಪರೀಕ್ಷೆಯಲ್ಲಿ ಪ್ರತಿಯೊಂದು ಸರಿಯುತ್ತರಕ್ಕೂ 3 ಅಂಕಗಳನ್ನು ಪಡೆದುಕೊಂಡು ಮತ್ತು ಪ್ರತಿಯೊಂದು ತಪ್ಪು ಉತ್ತರಕ್ಕೂ ಒಂದು ಅಂಕವನ್ನು ಕಳೆದುಕೊಂಡು, 40 ಅಂಕಗಳನ್ನು ಗಳಿಸಿದನು. ಒಂದು ವೇಳೆ ಪ್ರತಿಯೊಂದು ಸರಿ ಉತ್ತರಕ್ಕೆ 4 ಅಂಕಗಳನ್ನು ನೀಡಿ ಪ್ರತಿಯೊಂದು ತಪ್ಪು ಉತ್ತರಕ್ಕೆ 2 ಅಂಕಗಳನ್ನು ಕಳೆದರೆ, ಯಶ್ಗೆ 50 ಅಂಕಗಳು ಸಿಗುತ್ತಿತ್ತು. ಹಾಗಾದರೆ, ಪರೀಕ್ಷೆಯಲ್ಲಿ ಎಷ್ಟು ಪ್ರಶ್ನೆಗಳಿದ್ದುವು?
ಉತ್ತರ:
ಸರಿಯಾದ ಉತ್ತರಗಳ ಸಂಖ್ಯೆ x ಆಗಿರಲಿ ಮತ್ತು ತಪ್ಪಾದ ಉತ್ತರಗಳ ಸಂಖ್ಯೆ y ಆಗಿರಲಿ

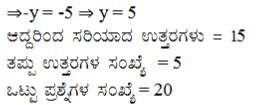
iv) ಹೆದ್ದಾರಿಯೊಂದರಲ್ಲಿ A ಮತ್ತು B ಎಂಬ ಎರಡು ಸ್ಥಳಗಳ ನಡುವಿನ ಅಂತರ 100km, ಏಕಕಾಲದಲ್ಲಿ ಒಂದು ಕಾರು A ಯಿಂದಲೂ ಇನ್ನೊಂದು ಕಾರು B ಯಿಂದಲೂ ಹೊರಡುತ್ತವೆ. ಕಾರುಗಳು ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ, ಬೇರೆ ಬೇರೆ ಜವದಲ್ಲಿ ಚಲಿಸಿದರೆ ಅವುಗಳು 5 ಗಂಟೆಗಳಲ್ಲಿ ಸಂಧಿಸುತ್ತವೆ. A ಕಾರು B ಯ ಕಡೆಗೆ, B ಕಾರು A ಯ ಚಲಿಸಿದರೆ, ಅವುಗಳು ಸಂಧಿಸಲು ಒಂದು ಗಂಟೆ ಬೇಕಾಗುತ್ತದೆ. ಹಾಗಾದರೆ ಕಾರುಗಳ ಜವಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಮೊದಲಿನ ಕಾರಿನ ವೇಗವು u km/h
ಮತ್ತೊಂದು ಕಾರಿನ ವೇಗವು v km/h
ಎರಡು ಕಾರುಗಳು ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಚಲಿಸಿದಾಗ ಅವುಗಳ ಜವವು = (u – v) km / h
ಎರಡು ಕಾರುಗಳು ಬೇರೆ ದಿಕ್ಕಿನಲ್ಲಿ ಚಲಿಸಿದಾಗ ಅವುಗಳ ಜವವು = (u + v) km / h
ಕೊಟ್ಟಿರುವ ಮಾಹಿತಿಗಳ ಪ್ರಕಾರ
5(u – v) = 100
u – v = 20 ….(1)
1(u + v) = 100 …..(2)
ಎರಡೂ ಸಮೀಕರಣಗಳನ್ನು ಕೂಡಿದಾಗ
2u = 120
u = 60km/hr
u = 60km / hr ನ್ನು ಸಮೀಕರಣ 2ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ
60 + v = 100
v = 40km/hr
ಮೊದಲನೆ ಕಾರಿನ ಜವವು = 60km/hr ಮತ್ತು ಮತ್ತೊಂದು ಕಾರಿನ ಜವವು 40 km/hr.
(v) ಒಂದು ಆಯತದ ಉದ್ದವನ್ನು 5 ಮಾನಗಳಷ್ಟು ಕಡಿಮೆಗೊಳಿಸಿ, ಅಗಲವನ್ನು 3 ಮಾನಗಳಷ್ಟು ಹೆಚ್ಚಿಸಿದರೆ ಅದರ ವಿಸ್ತೀರ್ಣವು 9 ಚದರ ಮಾನಗಳಷ್ಟು ಕಡಿಮೆಯಾಗುತ್ತದೆ. ಉದ್ದವನ್ನು 3 ಮಾನಗಳಷ್ಟು ಮತ್ತು ಅಗಲವನ್ನು 2 ಮಾನಗಳಷ್ಟು ಹೆಚ್ಚಿಸಿದರೆ, ವಿಸ್ತೀರ್ಣವು 67 ಚದರ ಮಾನಗಳಷ್ಟು ಹೆಚ್ಚಾಗುತ್ತದೆ. ಆಯತದ ಉದ್ದ, ಅಗಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಆಯತದ ಉದ್ದವು x ಆಗಿರಲಿ ಮತ್ತು ಅಗಲವು y ಆಗಿರಲಿ
ವಿಸ್ತೀರ್ಣ = xy
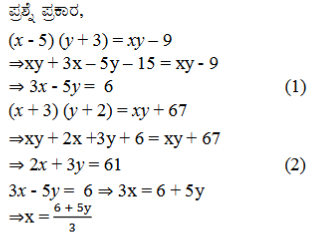

ಅಭ್ಯಾಸ 3.6
1. ಕೆಳಗಿನ ಸಮೀಕರಣಗಳನ್ನು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ ಜೋಡಿಗಳನ್ನಾಗಿ ಸಂಕ್ಷೇಪಿಸುವ ಮೂಲಕ ಬಿಡಿಸಿ.
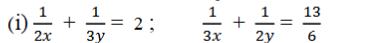
ಉತ್ತರ:
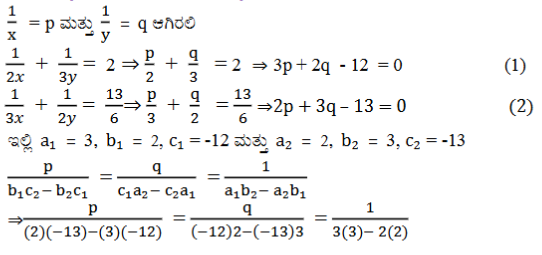
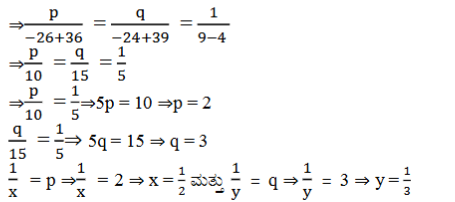
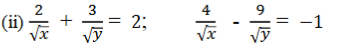
ಉತ್ತರ:
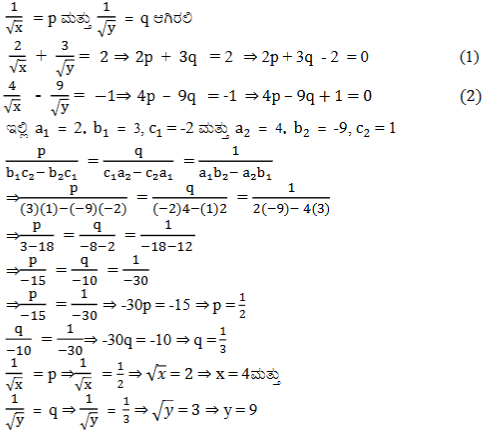
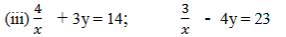
ಉತ್ತರ:
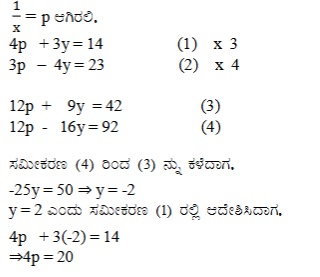
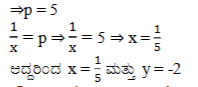
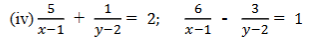
ಉತ್ತರ:
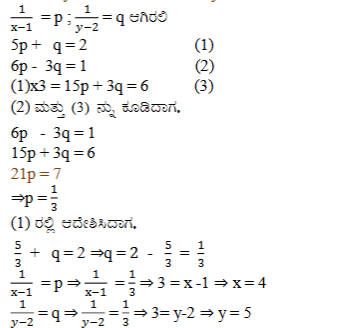

ಉತ್ತರ:
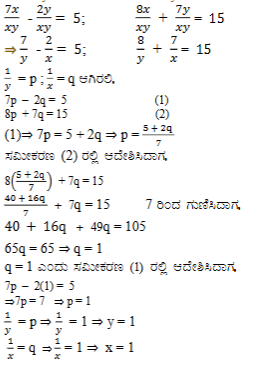
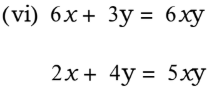
ಉತ್ತರ:


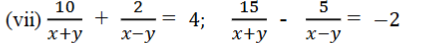
ಉತ್ತರ:
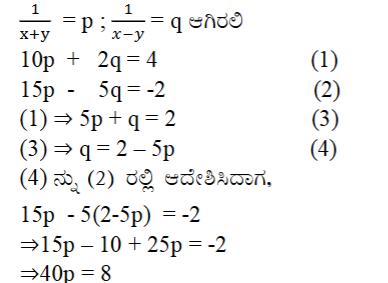
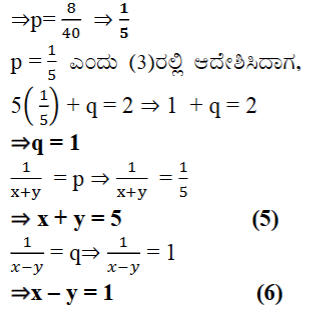

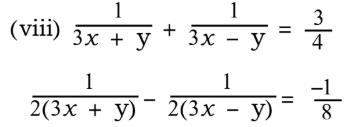
ಉತ್ತರ:

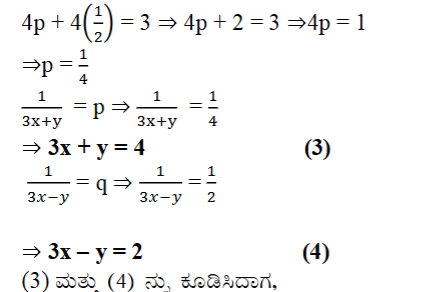

2. ಕೆಳಗಿನ ಸಮಸ್ಯೆಗಳಿಗೆ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ರಚಿಸಿ, ಅವುಗಳ ಪರಿಹಾರಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) ರೀತು ಪ್ರವಾಹದ ದಿಕ್ಕಿನಲ್ಲಿ 2 ಗಂಟೆಗಳಲ್ಲಿ 20 km ಮತ್ತು ಪ್ರವಾಹದ ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ 2 ಗಂಟೆಗಳಲ್ಲಿ 4 km ಸಂಚರಿಸುವಳು. ನಿಶ್ಚಲ ನೀರಿನಲ್ಲಿ ಅವಳು ಸಂಚರಿಸುವ ಜವ ಮತ್ತು ಹರಿಯುವ ನೀರಿನ ಜವಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ನಿಶ್ಚಲ ನೀರಿನಲ್ಲಿ ರೀತುವಿನ ಜವವು x km/h ಮತ್ತು ಪ್ರವಾಹದ ದಿಕ್ಕಿನಲ್ಲಿ ರೀತುವಿನ ಜವವು y km/h.
ಪ್ರವಾಹಕ್ಕೆ ವಿರುದ್ಧವಾಗಿ ರೀತುವಿನ ಜವವು = (x – y) km/h
ಪ್ರವಾಹದ ಕೆಳದಿಕ್ಕಿನಲ್ಲಿ ರೀತುವಿನ ಜವವು = (x + y)km/h
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ
2(x + y) = 20
x + y = 10 ….(1)
2(x – y) = 4
x – y = 2 ….(2)
ಸಮೀಕರಣ 1 ಮತ್ತು 2ನ್ನು ಕೂಡಿದಾಗ
x + y = 10
x – y = 2
2x = 12
x = 6
x = 6 ಸಮೀಕರಣ 1 ರಲ್ಲಿ ಆದೇಶಿಸಿದಾಗ
x + y = 10
6 + y = 10
y = 4
(ii) ಇಬ್ಬರು ಮಹಿಳೆಯರು, 5 ಪುರುಷರು ಒಟ್ಟಿಗೆ ಒಂದು ಕಸೂತಿ ಕಾರ್ಯವನ್ನು 4 ದಿನಗಳಲ್ಲಿ ಮುಗಿಸಬಲ್ಲರು. ಮೂರು ಮಹಿಳೆಯರು ಮತ್ತು 6 ಪುರುಷರು ಇದನ್ನು 3 ದಿನಗಳಲ್ಲಿ ಪೂರ್ಣಗೊಳಿಸಬಲ್ಲರು. ಒಬ್ಬ ಮಹಿಳೆ ಮಾತ್ರ ಈ ಕೆಲಸವನ್ನು ಪೂರ್ಣ ಮಾಡಿದರೆ ಎಷ್ಟು ದಿನಗಳು ಬೇಕಾಗುತ್ತವೆ? ಹಾಗೂ ಒಬ್ಬ ಪುರುಷ ಮಾತ್ರ ಈ ಕೆಲಸವನ್ನು ಪೂರ್ಣ ಮಾಡಿದರೆ ಎಷ್ಟು ದಿನಗಳು ಬೇಕಾಗುತ್ತವೆ?
ಉತ್ತರ:
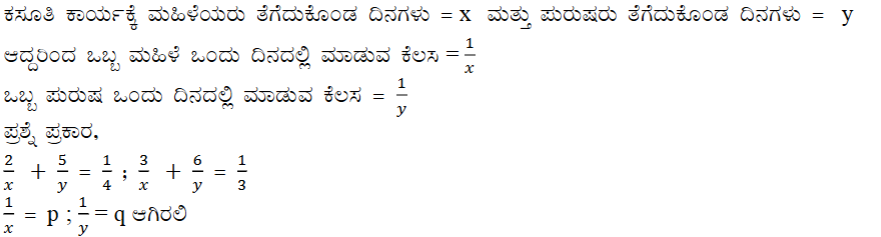
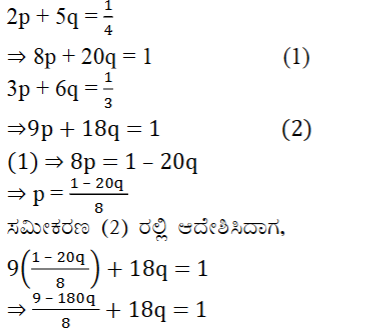

(iii) ರೂಹಿಯು 300 km ದೂರದಲ್ಲಿರುವ ತನ್ನ ಮನೆಯ ಕಡೆಗಿನ ಪ್ರಯಾಣದಲ್ಲಿ ಸ್ವಲ್ಪ ದೂರವನ್ನು ರೈಲಿನಲ್ಲಿಯೂ, ಉಳಿದ ದೂರವನ್ನು ಬಸ್ಸಿನಲ್ಲಿಯೂ ಕ್ರಮಿಸುವಳು. 60 km ನ್ನು ರೈಲಿನಲ್ಲೂ, ಉಳಿದ ಭಾಗವನ್ನು ಬಸ್ಸಿನಲ್ಲೂ ಪ್ರಯಾಣಿಸಿದರೆ ಅವಳು 4 ಗಂಟೆಗಳಲ್ಲಿ ತಲುಪುವಳು. 100 km ನ್ನು ರೈಲಿನಲ್ಲೂ, ಉಳಿದ ಭಾಗವನ್ನು ಬಸ್ಸಿನಲ್ಲೂ ಪ್ರಯಾಣಿಸಿದರೆ ಅವಳಿಗೆ ತಲುಪಲು 10 ನಿಮಿಷ ಹೆಚ್ಚು ಬೇಕಾಗುತ್ತದೆ. ಬಸ್ಸು ಮತ್ತು ರೈಲುಗಳ ಜವಗಳನ್ನು ಪ್ರತ್ಯೆಕವಾಗಿ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:


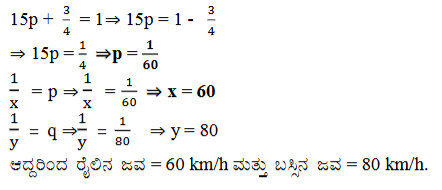
ಅಭ್ಯಾಸ 3.7 ( ಐಚ್ಛಿಕ)
1. ಅನಿ ಮತ್ತು ಬಿಜು ಎಂಬ ಇಬ್ಬರು ಗೆಳೆಯರ ವಯಸ್ಸುಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ 3 ವರ್ಷಗಳು. ಅನಿಯ ತಂದೆ ಧರಂರವರ ವಯಸ್ಸು ಅನಿಯ ವಯಸ್ಸಿನ ಎರಡರಷ್ಟು ಹಾಗೂ ಬಿಜುವಿನ ವಯಸ್ಸು ಅವನ ತಂಗಿ ಕ್ಯಾಥಿಯ ವಯಸ್ಸಿನ ಎರಡರಷ್ಟು. ಧರಂ ಮತ್ತು ಕ್ಯಾಥಿಯವರ ವಯಸ್ಸುಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ 30 ವರ್ಷಗಳು. ಅನಿ ಮತ್ತು ಬಿಜುವಿನ ವಯಸ್ಸುಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಅನಿ ಮತ್ತು ಬಿಜುವಿನ ವಯಸ್ಸುಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ 3 ವರ್ಷಗಳು
ಬಿಜುವು ಅನಿಗಿಂತ 3ವರ್ಷ ದೊಡ್ಡವನಾಗಿರಬಹುದು ಇಲ್ಲ ಅನಿಯು ಬಿಜುವಿಗಿಂತ 3ವರ್ಷ ದೊಡ್ಡವನಾಗಿರಬಹುದು.
ಎರಡೂ ಸಂದರ್ಭಗಳಲ್ಲೂ ಅನಿಯ ತಂದೆಯ ವಯಸ್ಸು ಕ್ಯಾಥಿಯ ವಯಸ್ಸಿಗು 30 ವರ್ಷಗಳು ಜಾಸ್ತಿ.
ಅನಿಯ ವಯಸ್ಸು x ಮತ್ತು ಬಿಜುವಿನ ವಯಸ್ಸು y ಆಗಿರಲಿ
ಅನಿಯ ತಂದೆ ಧರಂ ವಯಸ್ಸು = 2x ವರ್ಷಗಳು

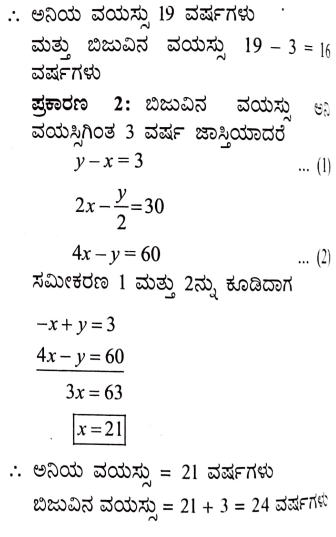
2. ಒಬ್ಬನು ಹೇಳುತ್ತಾನೆ, “ಗೆಳೆಯಾ, ನನಗೊಂದು ನೂರು ಕೊಡು. ಆಗ ನಾನು ನಿನಗಿಂತ ಎರಡುಪಟ್ಟು ಶ್ರೀಮಂತನಾಗುತ್ತೇನೆ”. ಇನ್ನೊಬ್ಬ ಉತ್ತರಿಸುತ್ತಾನೆ “ನೀನು ನನಗೆ 10 ಕೊಟ್ಟರೆ, ನಾನು ನಿನಗಿಂತ ಆರುಪಟ್ಟು ಶ್ರೀಮಂತನಾಗುತ್ತೇನೆ”. ಅವರಲ್ಲಿ ಪ್ರತಿಯೊಬ್ಬರ ಬಳಿ ಇರುವ ಬಂಡವಾಳವನ್ನು ಹೇಳಿ. [ಭಾಸ್ಕರ II ಇವರ ಬೀಜಗಣಿತ ಅಧ್ಯಾಯದಿಂದ]
ಉತ್ತರ:


3. ಒಂದು ರೈಲು ಸ್ಥಿರ ಜವದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ದೂರವನ್ನು ಕ್ರಮಿಸಿತು. ಒಂದು ವೇಳೆ ಅದು ಜವವನ್ನು 10 km/h ರಷ್ಟು ಹೆಚ್ಚಿಸಿದ್ದರೆ ಆ ದೂರವನ್ನು ಕ್ರಮಿಸಲು ಅದು ನಿಗದಿತ ಸಮಯಕ್ಕಿಂತ 2 ಗಂಟೆ ಕಡಿಮೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತಿತ್ತು. ಒಂದು ವೇಳೆ 10 km/h ರಷ್ಟು ಜವವನ್ನು ಕಡಿಮೆ ಮಾಡಿದ್ದರೆ ಅದೇ ದೂರವನ್ನು ಕ್ರಮಿಸಲು ನಿಗದಿತ ಸಮಯಕ್ಕಿಂತ 3 ಗಂಟೆ ಹೆಚ್ಚು ಬೇಕಾಗುತ್ತಿತ್ತು. ರೈಲು ಕ್ರಮಿಸಿದ ದೂರವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

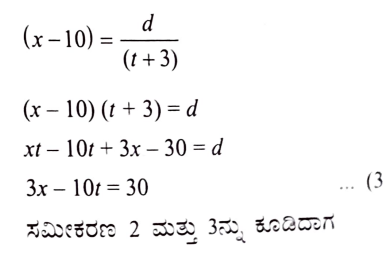

4. ಒಂದು ತರಗತಿಯಲ್ಲಿ ವಿದ್ಯಾರ್ಥಿಗಳನ್ನು ಹಲವು ಸಾಲುಗಳಲ್ಲಿ ನಿಲ್ಲಿಸಲಾಯಿತು. ಪ್ರತಿಯೊಂದು ಸಾಲಿನಲ್ಲಿ ಮೂರು ವಿದ್ಯಾರ್ಥಿಗಳು ಹೆಚ್ಚಿಗೆ ಇದ್ದರೆ ಒಂದು ಸಾಲು ಕಡಿಮೆಯಾಗುತ್ತಿತ್ತು. ಪ್ರತಿಯೊಂದು ಸಾಲಿನಲ್ಲಿ ಮೂರು ವಿದ್ಯಾರ್ಥಿಗಳು ಕಡಿಮೆ ಇದ್ದರೆ 2 ಸಾಲುಗಳು ಹೆಚ್ಚು ಬೇಕಾಗುತ್ತಿತ್ತು. ತರಗತಿಯಲ್ಲಿರುವ ವಿದ್ಯಾರ್ಥಿಗಳ ಒಟ್ಟು ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
ಅಡ್ಡಸಾಲಿನ ಸಂಖ್ಯೆ x ಆಗಿರಲಿ ಮತ್ತು ಅಡ್ಡಸಾಲಿನ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆಯು y ಆಗಿರಲಿ
ತರಗತಿಯ ಒಟ್ಟು ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ = ಅಡ್ಡಸಾಲಿನ ಸಂಖ್ಯೆ x ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ = x x y = xy ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ
ಪರಿಸ್ಥಿತಿ 1:
ಒಟ್ಟು ವಿಧ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ = (x – 1) (y + 3)
xy = xy – y + 3x – 3
3x – y – 3 = 0
3x – y = 3 … (1)
ಪರಿಸ್ಥಿತಿ 2:
ಒಟ್ಟು ವಿಧ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ = (x + 2)(y – 3)
xy = xy – 2y – 3x – 6
3x – 2y = – 6 ….(2)
ಸಮೀಕರಣ 2ನ್ನು 1ರಿಂದ ಕಳೆದಾಗ
(3x – y) – (3x – 2y) = 3 – (- 6)
– y + 2y = 3 + 6
y = 9
ಸಮೀಕರಣ 1 ನ್ನು ಬಳಸಿದಾಗ
3x – 9 = 3 → 3x = 9 + 3
3x =12 → x = 4
ಅಡ್ಡಸಾಲುಗಳ ಸಂಖ್ಯೆ = x=4
ಅಡ್ಡಸಾಲಿನ ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ = y = 9
ತರಗತಿಯಲ್ಲಿನ ಒಟ್ಟು ವಿದ್ಯಾರ್ಥಿಗಳ ಸಂಖ್ಯೆ xy = 4 x 9 = 36
5. ∆ABC ಯಲ್ಲಿ, ∠C = 3 ∠B = 2 (∠A+∠B) ಮೂರು ಕೋನಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

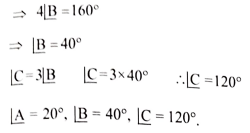
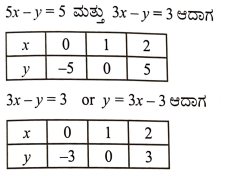
6. 5x – y = 5 ಮತ್ತು 3x – y = 3 ಈ ಸಮೀಕರಣಗಳ ನಕ್ಷೆಗಳನ್ನು ರಚಿಸಿರಿ. ಈ ರೇಖೆಗಳು ಮತ್ತು y ಅಕ್ಷದಿಂದ ಉಂಟಾಗುವ ತ್ರಿಭುಜದ ಶೃಂಗಬಿಂದುಗಳ ನಿರ್ದೇಶಾಂಕಗಳನ್ನು ಬರೆಯಿರಿ.
ಉತ್ತರ:
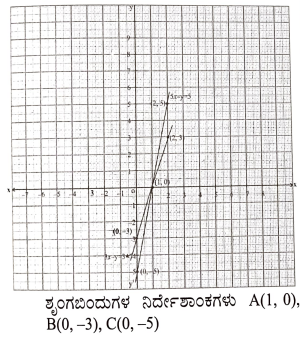
7. ಕೆಳಗಿನ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಗಳನ್ನು ಬಿಡಿಸಿರಿ.
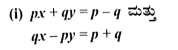
ಉತ್ತರ:
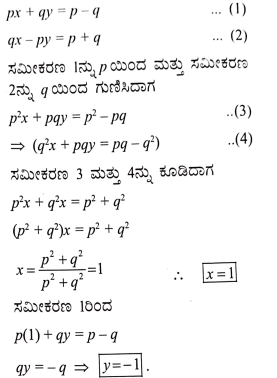
(ii) ax + by = c ಮತ್ತು bx + ay = 1 + c
ಉತ್ತರ:

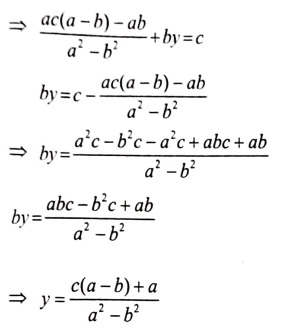
ಉತ್ತರ
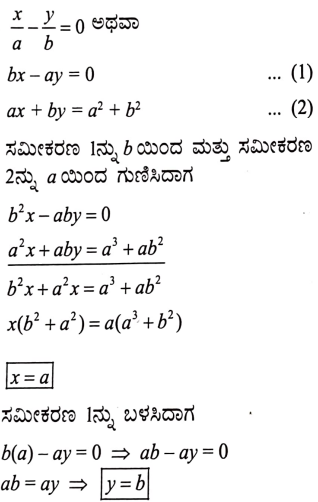
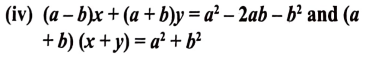
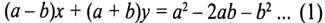
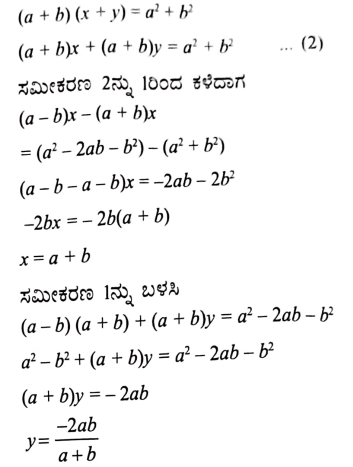
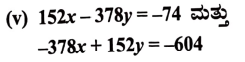
ಉತ್ತರ:

8. ABCD ಒಂದು ಚಕ್ರೀಯ ಚತುರ್ಭಜ ( ಚಿತ್ರ 3.7 ನ್ನು ನೋಡಿರಿ) ಚಕ್ರೀಯ ಚತುರ್ಭುಜದ ಕೋನಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
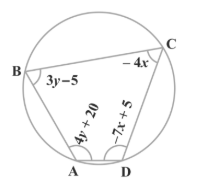
ಉತ್ತರ:
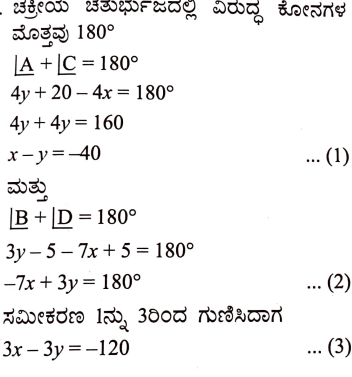
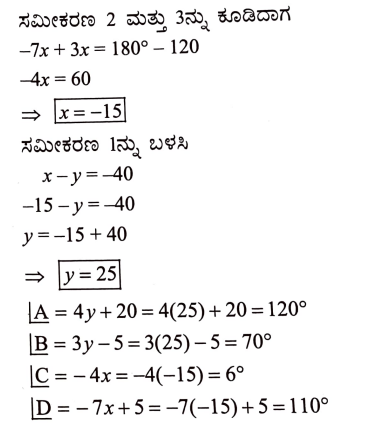
ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. ವರ್ಜಿಸುವ ವಿಧಾನ: ಚರಾಕ್ಷರವನ್ನು ವರ್ಜಿಸುವ (ಅಂದರೆ ರದ್ದುಗೊಳಿಸುವ) ಮತ್ತೊಂದು ವಿಧಾನವನ್ನು ನಾವೀಗ ನೋಡೋಣ. ಇದು ಕೆಲವೊಮ್ಮೆ ಆದೇಶ ವಿಧಾನಕ್ಕಿಂತ ಹೆಚ್ಚು ಅನುಕೂಲಕರವಾಗಿದೆ.
2. ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಈ ಜೋಡಿಗೆ ಒಂದು ಮತ್ತು ಒಂದೇ ಒಂದು ಪರಿಹಾರವಿದೆ.
3. ಒಂದು ಸಮತಲದ ಮೇಲೆ ಎರಡು ಸರಳ ರೇಖೆಗಳನ್ನು ಕೊಟ್ಟಾಗ ಒಂದು ಸಾಧ್ಯತೆ ಮಾತ್ರ ಇರುತ್ತದೆ.
(1) ಎರಡು ರೇಖೆಗಳು ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸುತ್ತವೆ.
(11) ಎರಡು ರೇಖೆಗಳು ಒಂದನ್ನೊಂದು ಛೇದಿಸುವುದಿಲ್ಲ. ಅಂದರೆ ಅವುಗಳು ಸಮಾಂತರ,
(11) ಎರಡು ರೇಖೆಗಳು ಐಕ್ಯಗೊಂಡಿರುತ್ತವೆ.
4. ax + by + c = 0 ರೂಪದಲ್ಲಿ ಬರೆಯಬಹುದಾದ a, b ಮತ್ತು c ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳಾಗಿರುವ a ಮತ್ತು b ಈ ಎರಡೂ ಸೊನ್ನೆ ಅಲ್ಲದಿರುವ ಯಾವುದೇ ಸಮೀಕರಣವನ್ನು ಎರಡು ಚರಾಕ್ಷಿಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣ ಎನ್ನುತ್ತೇವೆ.
5. ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ರೇಖೆಗಳ ವರ್ತನೆ ಮತ್ತು ಪರಿಹಾರಗಳ ಇರುವಿಕೆಯನ್ನು ಈ ಮುಂದಿನಂತೆ ನಾವೀಗ ಸಾರಾಂಶೀಕರಿಸಬಹುದು.
(i) ಎರಡು ಸರಳರೇಖೆಗಳು ಒಂದು ಬಿಂದುವಿನಲ್ಲಿ ಛೇದಿಸಬಹುದು. ಇಂತಹ ಪ್ರಕರಣದಲ್ಲಿ ಸಮೀಕರಣಗಳ ಜೋಡಿಗೆ ಅನನ್ಯ ಪರಿಹಾರವಿರುತ್ತದೆ. (ಸಮೀಕರಣಗಳ ಸ್ಥಿರ ಜೋಡಿ)
(ii) ರೇಖೆಗಳು ಸಮಾಂತರವಾಗಿರಬಹುದು. ಇಂತಹ ಪ್ರಕರಣದಲ್ಲಿ ಸಮೀಕರಣಗಳಿಗೆ ಪರಿಹಾರವಿಲ್ಲ. (ಸಮೀಕರಣಗಳ ಆಸ್ಥಿರ ಜೋಡಿ)
(iii) ರೇಖೆಗಳು ಐಕ್ಯಗೊಳ್ಳಬಹುದು. ಇಂತಹ ಪ್ರಕರಣದಲ್ಲಿ ಸಮೀಕರಣಗಳಿಗೆ ಅಪರಿಮಿತ ಸಂಖ್ಯೆಯ ಪರಿಹಾರಗಳಿರುತ್ತವೆ.
6. ಎರಡು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳೂ x ಮತ್ತು y ಗಳೆಂಬ ಚರಾಕ್ಷರಗಳನ್ನು ಮಾತ್ರ ಹೊಂದಿವೆ. ಇಂತಹ ಸಮೀಕರಣಗಳನ್ನು ಎರಡು ಚಿರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿ ಎನ್ನುತ್ತೇವೆ.
7. ವರ್ಜಿಸುವ ವಿಧಾನದಲ್ಲಿರುವ ಈ ಹಂತಗಳನ್ನು ಪಟ್ಟಿ ಮಾಡೋಣ.
ಹಂತ 1: ಚರಾಕ್ಷರಗಳಲ್ಲಿ ಒಂದರ (x ಅಥವಾ y ಯ) ಸಹಗುಣಕಗಳು ಸಮವಾಗುವ ಹಾಗೆ, “ಎರಡು ಸಮೀಕರಣಗಳಿಗೂ ಸೂಕ್ತವಾದ ಒಂದು ಸ್ಥಿರಾಂಕದಿಂದ ಗುಣಿಸಿ (ಸೊನ್ನೆಯನ್ನು ಬಿಟ್ಟು),
ಹಂತ 2: ಆ ಬಳಿಕ ಒಂದು ಚರಾಕ್ಷರವು ವರ್ಜಿಸಲ್ಪಡುವಂತೆ ಒಂದು ಸಮೀಕರಣಕ್ಕೆ ಮತ್ತೊಂದನ್ನು ಕೂಡಿಸಿರಿ ಅಥವಾ ಕಳೆಯಿರಿ. ಈಗ ಒಂದೇ ಚರಾಕ್ಷರವಿರುವ ಸಮೀಕರಣವು ನಿಮಗೆ ದೊರೆತರೆ 3ನೇ ಹಂತಕ್ಕೆ ಹೋಗಿ
2ನೇ ಹಂತದಲ್ಲಿ ಯಾವುದೇ ಚರಾಕ್ಷರಗಳಿಲ್ಲದ ಒಂದು ನೈಜ ಹೇಳಿಕೆ ನಮಗೆ ದೊರೆತರೆ ಆಗ ಸಮೀಕರಣಗಳ ಮೂಲ ಜೋಡಿಗೆ ಅಪರಿಮಿತ ಸಂಖ್ಯೆಯ ಪರಿಹಾರಗಳಿರುತ್ತವೆ.
2ನೇ ಹಂತದಲ್ಲಿ ಯಾವುದೇ ಚರಾಕ್ಷರಗಳಿಲ್ಲದ ಒಂದು ಅಸಂಬದ್ಧ ಹೇಳಿಕೆ ನಮಗೆ ದೊರೆತರೆ, ಆಗ ಸಮೀಕರಣಗಳ ಮೂಲ ಜೋಡಿಗೆ ಯಾವುದೇ ಪರಿಹಾರವಿಲ್ಲ. ಅಂದರೆ ಅದು ಅಸ್ಥಿರ
ಹಂತ 3: ಹೀಗೆ ದೊರೆತ ಒಂದು ಚರಾಕ್ಷರದ (x ಅಥವಾ ) ಸಮೀಕರಣವನ್ನು ಬಿಡಿಸಿ ಅದರ ಬೆಲೆ ಕಂಡು ಹಿಡಿಯಿರಿ.
ಹಂತ 4: x ನ (ಅಥವಾ y ಯ) ಈ ಬೆಲೆಯನ್ನು ಮೂಲ ಸಮೀಕರಣವೊಂದರಲ್ಲಿ ಆದೇಶಿಸಿ. ಇನ್ನೊಂದು ಚರಾಕ್ಷರದ ಬೆಲೆಯನ್ನು ಪಡೆಯಿರಿ.
8. ಒಂದು ಚರಾಕ್ಷರವನ್ನು ಮೊದಲು ವರ್ಜಿಸಿ ಒಂದೇ ಚರಾಕ್ಷರದ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣವನ್ನು ನಾವು ಪಡೆಯುತ್ತೇವೆ.
9. ಎರಡು ಸಮಾನ ಚರಾಕ್ಷರಗಳಿರುವ ಎರಡು ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳನ್ನು ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿ ಎನ್ನುತ್ತೇವೆ. ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಯ ಅತ್ಯಂತ ಸಾಮಾನ್ಯ ರೂಪವು
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
a1, a2, b1, b2, c1, c2 ಗಳು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು
10. ಎರಡು ಚರಾಕ್ಷರಗಳಿರುವ ರೇಖಾತ್ಮಕ ಸಮೀಕರಣಗಳ ಜೋಡಿಯನ್ನು
(i) ನಕ್ಷಾ ವಿಧಾನದಿಂದ
(ii) ಬೀಜಗಣಿತೀಯ ವಿಧಾನದಿಂದ ಪ್ರತಿನಿಧಿಸಬಹುದು ಮತ್ತು ಬಿಡಿಸಬಹುದು.
11. ದತ್ತ ಸಮೀಕರಣಗಳ ಜೋಡಿಯು ಅನನ್ಯ ಪರಿಹಾರವನ್ನು ಹೊಂದಿರುತ್ತದೆ.
ಇತರೆ ವಿಷಯಗಳು :
10ನೇ ತರಗತಿ ಗಣಿತ ವೃತ್ತಗಳು ನೋಟ್ಸ್
10ನೇ ತರಗತಿ ಗಣಿತ ತ್ರಿಭುಜಗಳು ನೋಟ್ಸ್
