10th Standard Varga Samikaranagalu Maths Notes Question Answer Guide Extract Mcq Pdf Download Kannada Medium Karnataka State Syllabus 2025 10ನೇ ತರಗತಿ ವರ್ಗ ಸಮೀಕರಣ 10ನೇ ತರಗತಿ ಗಣಿತ ವರ್ಗ ಸಮೀಕರಣಗಳು ನೋಟ್ಸ್ ಪ್ರಶ್ನೋತ್ತರಗಳು, ಗಣಿತ ನೋಟ್ಸ್ 10ನೇ ತರಗತಿ pdf, 10th standard maths chapter 10 notes, class 10 maths chapter 10 pdf kannada medium, kseeb solutions for class 10 maths in kannada,10th standard maths 10th lesson in kannada sslc maths notes kannada medium pdf download.
ಘಟಕ 10 – ವರ್ಗ ಸಮೀಕರಣಗಳು
ಅಭ್ಯಾಸ – 10.1
1. ಈ ಕೆಳಗಿನವುಗಳು ವರ್ಗ ಸಮೀಕರಣಗಳೇ ಎಂಬುದನ್ನು ಪರೀಕ್ಷಿಸಿ.
i) (x + 1)2 = 2(x – 3)
(ii) x2 – 2x = (-2)(3 – x)
(iii) (x – 2) (x + 1) =(x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x(x + 5)
(v) (2x – 1) (x – 3) = (x + 5) (x – 1)
(vi) x2 + 3x + 1 =(x – 2)2
(vii) (x+2)3 = 2x(x2 – 1)
(viii) x3 – 4x2 – x + 1 = (x – 2)3
ಉತ್ತರ:


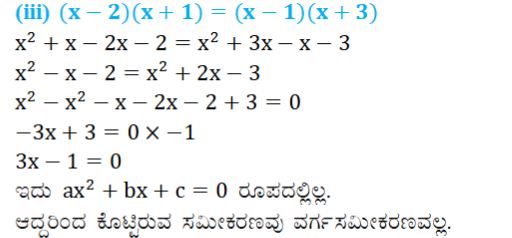
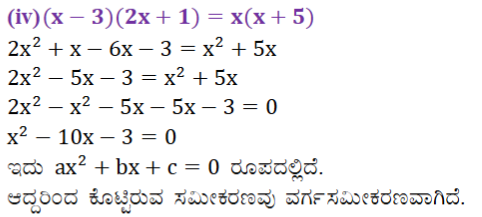
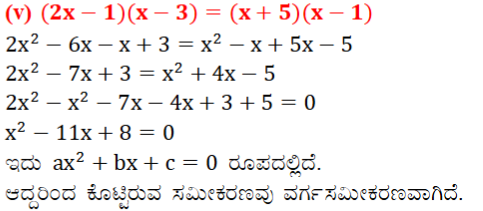
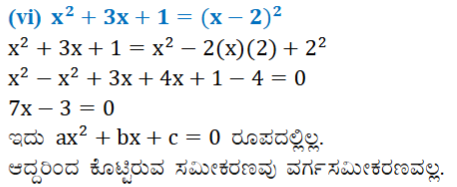
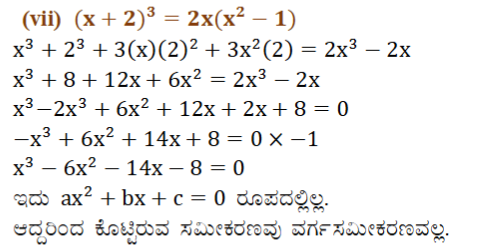
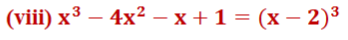
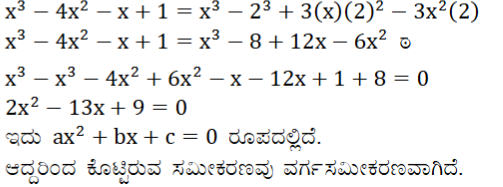
2. ಈ ಕೆಳಗಿನ ಸನ್ನಿವೇಶಗಳನ್ನು ವರ್ಗ ಸಮೀಕರಣಗಳ ರೂಪದಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಿ.
(i) ಒಂದು ಆಯತಾಕಾರದ ನಿವೇಶನದ ವಿಸ್ತೀರ್ಣವು 528m’ ಆಗಿದೆ. ನಿವೇಶನದ ಉದ್ದವು (ಮೀಟರ್ಗಳಲ್ಲಿ) ಅದರ ಅಗಲದ ಎರಡಷ್ಟಕ್ಕಿಂತ ಒಂದು ಹೆಚ್ಚಾಗಿದೆ. ಆ ನಿವೇಶನದ ಉದ್ದ ಮತ್ತು ಅಗಲಗಳನ್ನು ನಾವು ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ.
ಉತ್ತರ:
ಆಯತಾಕಾರದ ನಿವೇಶನದ ಅಗಲವು xm ಉದ್ದ = (2x+1)
∴ ಆಯತದ ವಿಸ್ತೀರ್ಣ = l x b = 528 m2
∴ x(2x + 1) = 528
∴ 2x2 + x – 528 = 0
∴ ಉದ್ದ ಮತ್ತು ಹಗಲಗಳು ನಿವೇಶನದ ಸಮೀಕರಣವನ್ನು ಅನ್ವಯಿಸುತ್ತವೆ.
ವರ್ಗಸಮೀಕರಣದ ರೂಪ 2x2 + x – 528 = 0
(ii) ಎರಡು ಅನುಕ್ರಮ ಧನ ಪೂರ್ಣಾಂಕಗಳ ಗುಣಲಬ್ಬವು 306 ಆಗಿದೆ. ನಾವು ಆ ಪೂರ್ಣಾಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಬೇಕಾಗಿದೆ.
ಉತ್ತರ:
ಮೊದಲ ಧನ ಪೂರ್ಣಾಂಕವು =x
∴ ಎರಡನೇ ಧನ ಪೂರ್ಣಾಂಕವು = (x + 1)
ಪ್ರಶ್ನೆಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ
x(x + 1) = 306
∴ x2 + x = 306
∴ x2 + x – 306 = 0
∴ ಧನ ಪೂರ್ಣಾಂಕಗಳು ಸಮೀಕರಣ x2 + x – 306 = 0
ಬೇಕಾದ ವರ್ಗಸಮೀಕರಣ x2 + x – 306 = 0
(iii) ರೋಹನನ ತಾಯಿಯು ಅವನಿಗಿಂತ 26 ವರ್ಷ ದೊಡ್ಡವಳಾಗಿದ್ದಾಳೆ. 3 ವರ್ಷಗಳ ನಂತರ ಅವರ ವಯಸ್ಸುಗಳ (ವರ್ಷಗಳಲ್ಲಿ) ಗುಣಲಬ್ಧವು 360 ಆಗುತ್ತದೆ. ನಾವು ರೋಹನನ ಈಗಿನ ವಯಸ್ಸನ್ನು ಕಂಡುಹಿಡಿಯಲು ಬಯಸುತ್ತೇವೆ.
ಉತ್ತರ:
ರೋಹನನ ವಯಸ್ಸು x ವರ್ಷಗಳು
ಅವನ ತಾಯಿಯ ವಯಸ್ಸು = (x + 26)
ಮೂರು ವರ್ಷಗಳ ನಂತರ ರೋಹನನ ವಯಸ್ಸು = (x + 3) ವರ್ಷಗಳು
ಅವನ ತಾಯಿಯ ವಯಸ್ಸು = (x + 26 + 3) = (x+29) ವರ್ಷಗಳುಪ್ರಶ್ನೆ
ಯಲ್ಲಿನ ಹೇಳಿಕೆಯಂತೆ
(x + 3)(x + 29) = 360
x2 + 29x + 3x + 87 = 360
∴ x2 + 32x – 273 = 0
ರೋಹನನ ವಯಸ್ಸು ಸಮೀಕರಣವನ್ನು ಖಾತ್ರಿಪಡಿಸುತ್ತದೆ.
ಬೇಕಾದ ವರ್ಗಸಮೀಕರಣ x2 + 32x – 273 = 0
(iv)ಒಂದು ರೈಲು ಏಕರೂಪದ ಜವದಲ್ಲಿ ಚಲಿಸಿ, 480km ದೂರವನ್ನು ಕ್ರಮಿಸುತ್ತದೆ. ಅದರ ಜವವು 8km/h ಕಡಿಮೆ ಆಗಿದ್ದರೆ, ಅಷ್ಟೇ ದೂರವನ್ನು ಕ್ರಮಿಸಲು ರೈಲು 3 ಘಂಟೆ ಹೆಚ್ಚಾಗಿ ತೆಗೆದುಕೊಳ್ಳುತ್ತಿತ್ತು. ನಾವು ರೈಲಿನ ಜವವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಬಯಸುತ್ತೇವೆ.
ಉತ್ತರ:
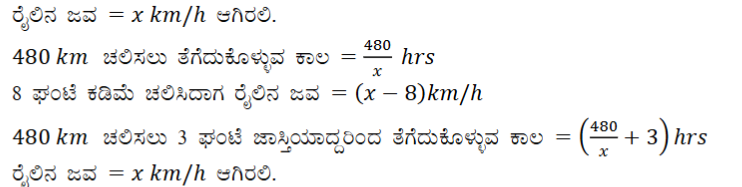

2. ಅಪವರ್ತನ ವಿಧಾನದಿಂದ ಕೆಳಗಿನ ವರ್ಗ ಸಮೀಕರಣಗಳ ಮೂಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
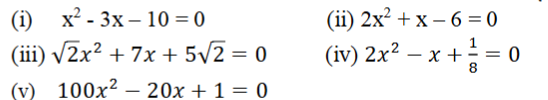
ಉತ್ತರ:


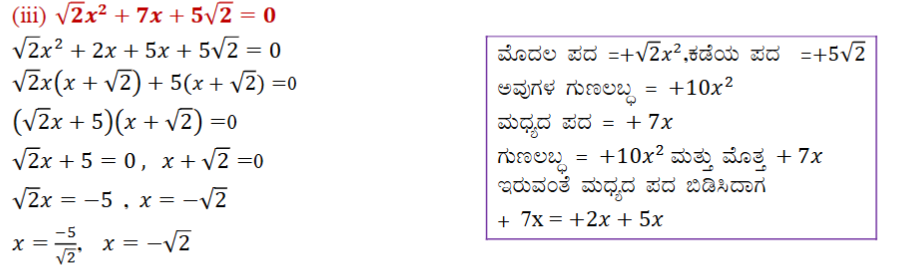

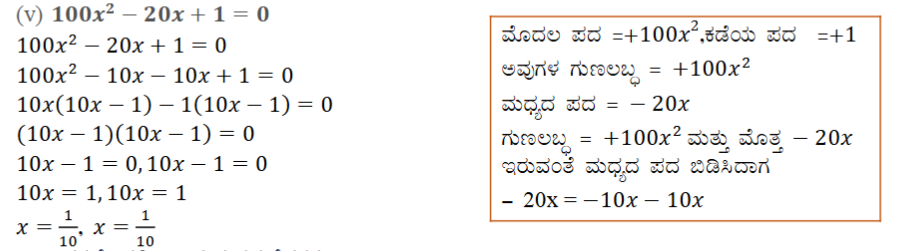
2. ಉದಾಹರಣೆ1 ರಲ್ಲಿ ನೀಡಿರುವ ಸಮಸ್ಯೆಗಳನ್ನು ಬಿಡಿಸಿ.
(i) (1) ಜಾನ್ ಮತ್ತು ಜೀವಂತಿ ಇವರಿಬ್ಬರ ಬಳಿ ಇರುವ ಒಟ್ಟು ಗೋಲಿಗಳ ಸಂಖ್ಯೆ 45 ಆಗಿದೆ. ಇವರಿಬ್ಬರೂ ತಲಾ 5 ಗೋಲಿಗಳನ್ನು ಕಳೆದುಕೊಂಡರೆ ಇವರ ಬಳಿ ಇರುವ ಗೋಲಿಗಳ ಸಂಖ್ಯೆಗಳ ವರ್ಗ ಸಮೀಕರಣಗಳು 23 ಗುಣಲಬ್ಧ 124 ಆಗುತ್ತದೆ. ಹಾಗಾದರೆ ಆರಂಭದಲ್ಲಿ ಅವರ ಬಳಿ ಇದ್ದ ಗೋಲಿಗಳ ಸಂಖ್ಯೆ ಎಷ್ಟು ಎಂಬುದನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
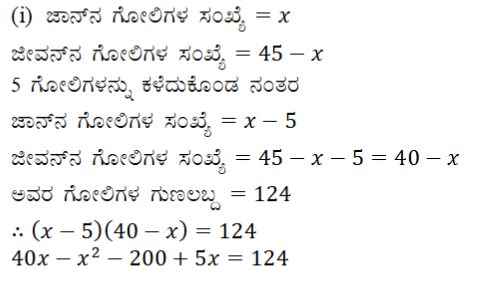
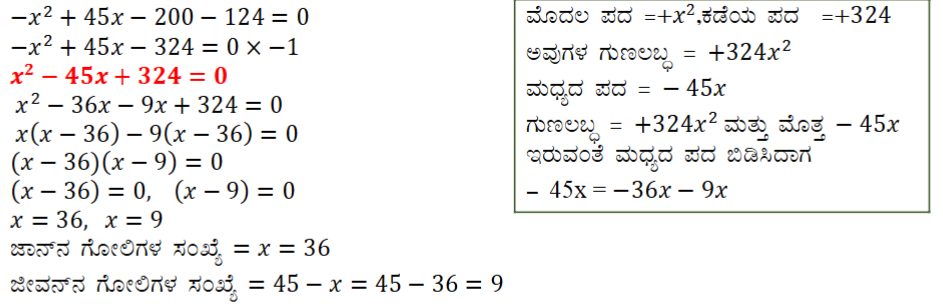
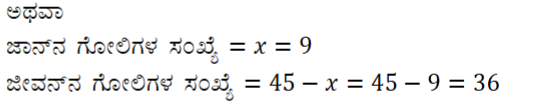
(ii) ಒಂದು ಗುಡಿ ಕೈಗಾರಿಕೆಯು ಒಂದು ದಿನದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ಆಟಿಕೆಗಳನ್ನು ತಯಾರಿಸುತ್ತದೆ. ಪ್ರತಿ ಆಟಿಕೆಯ ಉತ್ಪಾದನಾ ವೆಚ್ಚವು, (ರೂಪಾಯಿಗಳಲ್ಲಿ) 55ರಿಂದ, ಒಂದು ದಿನದಲ್ಲಿ ಉತ್ಪಾದಿಸಿದ ಆಟಿಕೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಕಳೆದಷ್ಟಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ. ಒಂದು ನಿರ್ದಿಷ್ಟ ದಿನದಲ್ಲಿ ಆಟಿಕೆಗಳ ಒಟ್ಟು ಒತ್ಪಾದನಾ ವೆಚ್ಚವು ₹ 750 ಆಗಿದ್ದರೆ, ಆ ದಿನ ಉತ್ಪಾದಿಸಿದ ಆಟಿಕೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

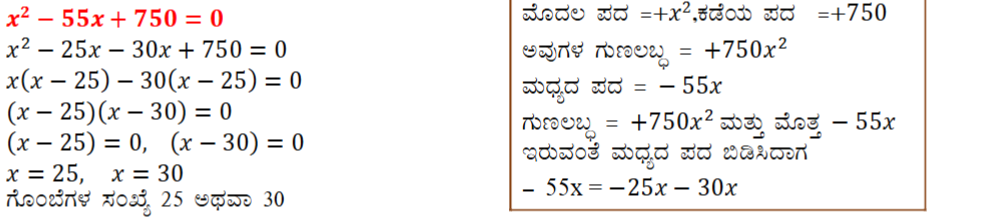
3. ಎರಡು ಸಂಖ್ಯೆಗಳ ಮೊತ್ತ 27 ಮತ್ತು ಗುಣಲಬ್ಧ 182 ಆದರೆ ಆ ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

4. ಎರಡು ಅನುಕ್ರಮ ಧನ ಪೂರ್ಣಾಂಕಗಳ ವರ್ಗಗಳ ಮೊತ್ತವು 365 ಆದರೆ ಆ ಸಂಖ್ಯೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

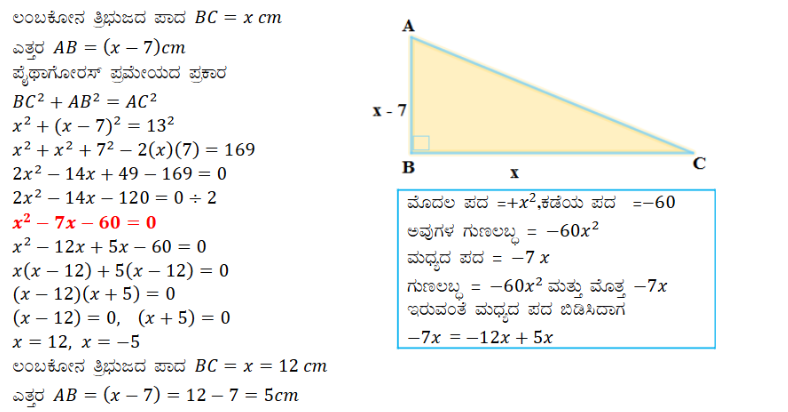
5. ಒಂದು ಲಂಬಕೋನ ತ್ರಿಭುಜದ ಎತ್ತರವು ಅದರ ಪಾದಕ್ಕಿಂತ 7cm ಕಡಿಮೆ ಇದೆ. ಅದರ ವಿಕರ್ಣದ ಉದ್ದವು 13cm ಆದರೆ ಉಳಿದೆರಡು ಬಾಹುಗಳ ಉದ್ದಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
6. ಒಂದು ಗುಡಿ ಕೈಗಾರಿಕೆಯು ಒಂದು ದಿನದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ಮಡಿಕೆಗಳನ್ನು ತಯಾರಿಸುತ್ತದೆ. ಒಂದು ನಿರ್ದಿಷ್ಟ ದಿನದಲ್ಲಿ, ಪ್ರತಿ ಮಡಿಕೆಯ ಉತ್ಪಾದನಾ ವೆಚ್ಚವು (ರೂಪಾಯಿಗಳಲ್ಲಿ), ಆ ದಿನ ತಯಾರಿಸಿದ ಮಡಿಕೆಗಳ ಸಂಖ್ಯೆಯ ಎರಡರಷ್ಟಕ್ಕಿಂತ 3 ಹೆಚ್ಚಾಗಿರುವುದನ್ನು ಗಮನಿಸಲಾಯಿತು. ಆ ದಿನದ ಒಟ್ಟು ಉತ್ಪಾದನಾ ವೆಚ್ಚವು ರೂ 90 ಆದರೆ ಆ ದಿನ ತಯಾರಿಸಿದ ಮಡಿಕೆಗಳ ಸಂಖ್ಯೆಯನ್ನು ಹಾಗೂ ಪ್ರತಿ ಮಡಿಕೆಯ ವೆಚ್ಚವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
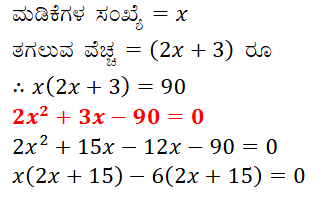

ಅಭ್ಯಾಸ 10.3
1. ಈ ಕೆಳಗಿನ ವರ್ಗ ಸಮೀಕರಣಗಳು ವಾಸ್ತವ ಮೂಲಗಳನ್ನು ಹೊಂದಿದ್ದರೆ, ವರ್ಗ ಪೂರ್ಣಗೊಳಿಸುವ ವಿಧಾನದಿಂದ ಅವುಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(1) 2x2 – 7x + 3 = 0
(ii) 2x2 + x – 4 = 0
(iii) 4x2 + 4√3x + 3 = 0
(iv) 2x2 + x + 4 = 0
ಉತ್ತರ:
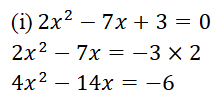

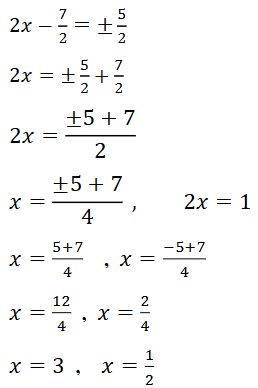
(ii) 2x2 + x – 4 = 0
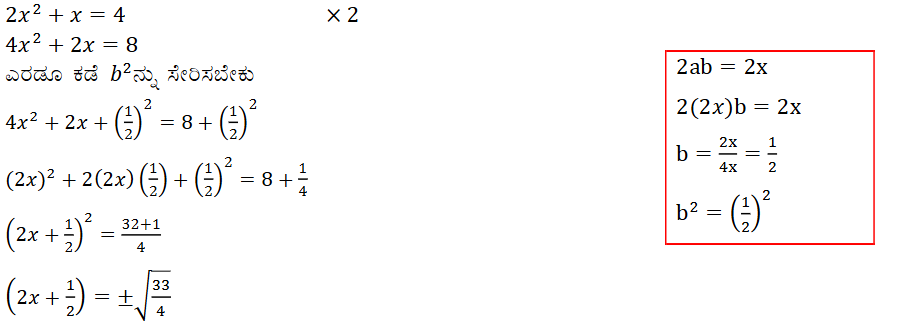
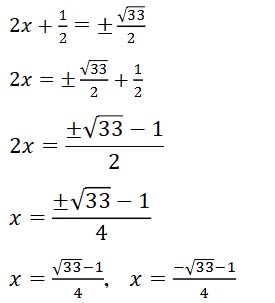
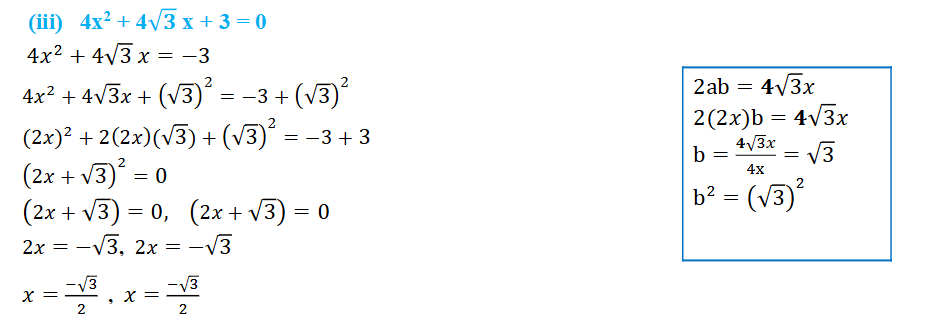
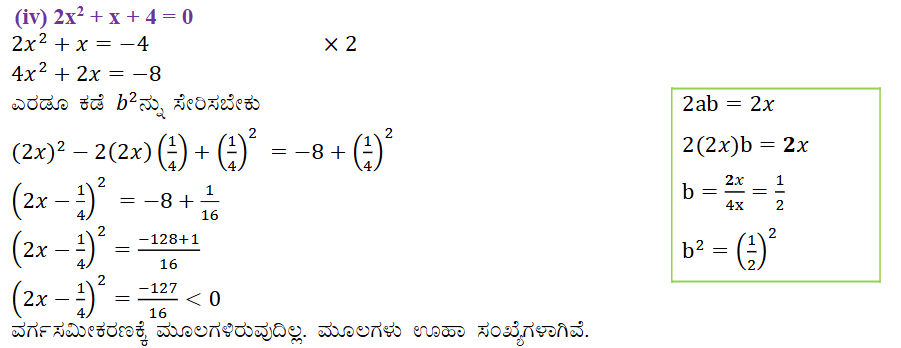
2. ಪ್ರಶ್ನೆ 1ರಲ್ಲಿ ನೀಡಲಾದ ವರ್ಗ ಸಮೀಕರಣಗಳ ಮೂಲಗಳನ್ನು ವರ್ಗಸಮೀಕರಣದ ಸೂತ್ರದ ಸಹಾಯದಿಂದ ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
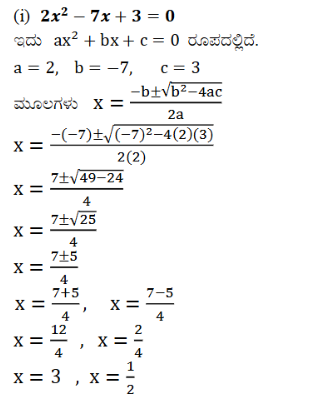
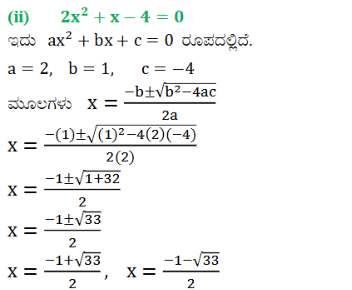
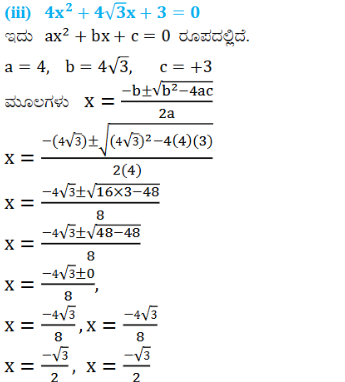

3. ಈ ಕೆಳಗಿನ ಸಮೀಕರಣಗಳ ಮೂಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

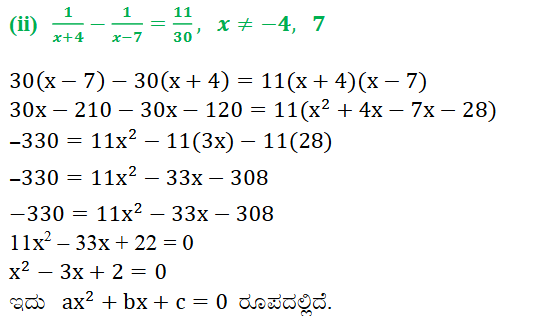
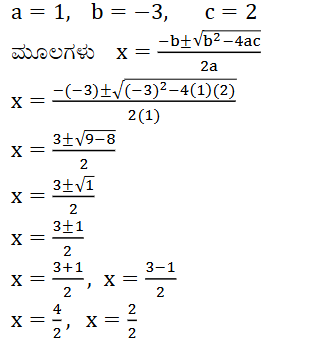
4. ಮೂರು ವರ್ಷಗಳ ಹಿಂದಿನ ರೆಹಮಾನನ ವಯಸ್ಸು (ವರ್ಷಗಳಲ್ಲಿ) ಮತ್ತು 5 ವರ್ಷಗಳ ನಂತರದ ಅವನ ವಯಸ್ಸು ಇವುಗಳ ವ್ಯುತ್ಕ್ರಮಗಳ ಮೊತ್ತ 1/3 ಆದರೆ ಅವನ ಈಗಿನ ವಯಸ್ಸನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
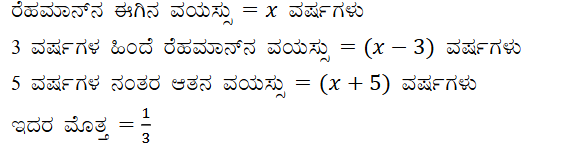
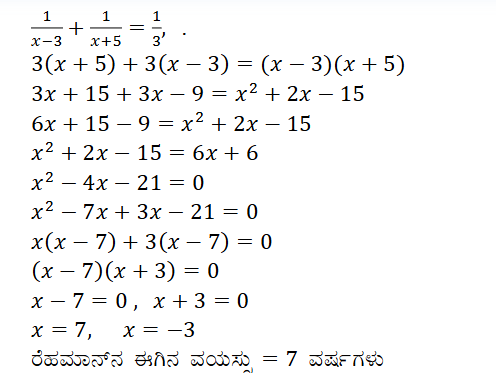
5. ಒಂದು ಕಿರು ಪರೀಕ್ಷೆಯಲ್ಲಿ ಶಿಫಾಲಿಯು ಗಣಿತ ಮತ್ತು ಇಂಗ್ಲೀಷ್ ವಿಷಯಗಳಲ್ಲಿ ಪಡೆದ ಅಂಕಗಳ ಮೊತ್ತ 30 ಆಗಿದೆ. ಅವಳು ಗಣಿತದಲ್ಲಿ ಇನ್ನೂ 2 ಹೆಚ್ಚು ಅಂಕಗಳನ್ನು ಮತ್ತು ಇಂಗ್ಲೀಷ್ನಲ್ಲಿ 3 ಕಡಿಮೆ ಅಂಕಗಳನ್ನು ಪಡೆದಿದ್ದರೆ, ಆಗ ಆ ಅಂಕಗಳ ಗುಣಲಬ್ಧ 210 ಆಗುತ್ತಿತ್ತು. ಅವಳು ಗಣಿತ ಮತ್ತು ಇಂಗ್ಲೀಷ್ನಲ್ಲಿ ಪಡೆದ ಅಂಕಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

6. ಒಂದು ಆಯತಾಕಾರದ ಹೊಲದ ಕರ್ಣವು ಅದರ ಚಿಕ್ಕ ಬಾಹುವಿಗಿಂತ 60 m ಹೆಚ್ಚಾಗಿದೆ. ಅದರ ದೊಡ್ಡ ಬಾಹುವು ಚಿಕ್ಕ ಬಾಹುವಿಗಿಂತ 30 m ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಆ ಹೊಲದ ಬಾಹುಗಳ ಉದ್ದಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
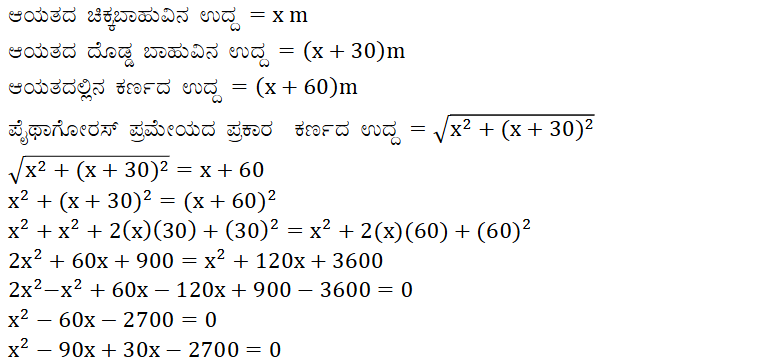
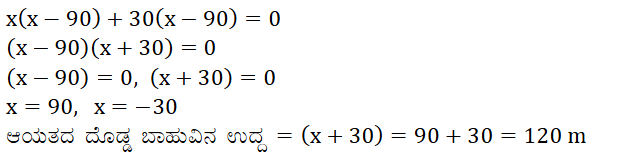
7. ಎರಡು ಸಂಖ್ಯೆಗಳ ವರ್ಗಗಳ ವ್ಯತ್ಯಾಸವು 180 ಆಗಿದೆ. ಚಿಕ್ಕ ಸಂಖ್ಯೆಯ ವರ್ಗವು ದೊಡ್ಡ ಸಂಖ್ಯೆಯ ಎಂಟರಷ್ಟಿದ್ದರೆ ಆ ಎರಡು ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

8. ಒಂದು ರೈಲು 360 km ದೂರವನ್ನು ಏಕರೂಪ ಜವದೊಂದಿಗೆ ಕ್ರಮಿಸುತ್ತದೆ. ಅದರ ಜವವು 5 km/h ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಅಷ್ಟೇ ದೂರವನ್ನು ಕ್ರಮಿಸಲು ಅದು 1 ಘಂಟೆ ಕಡಿಮೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತಿತ್ತು. ರೈಲಿನ ಜವವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ
ಉತ್ತರ:


ಉತ್ತರ:
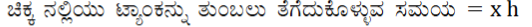

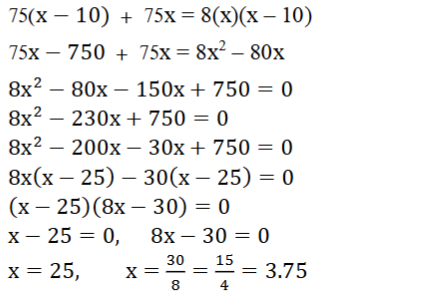

10. ಒಂದು ಎಕ್ಸಪ್ರೆಸ್ ರೈಲು ಮೈಸೂರು ಮತ್ತು ಬೆಂಗಳೂರಿನ ನಡುವಿನ 132 km ದೂರವನ್ನು ಕ್ರಮಿಸಲು ಪ್ಯಾಸೆಂಜರ್ ರೈಲಿಗಿಂತ 1 ಘಂಟೆ ಕಡಿಮೆ ಸಮಯವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ (ಮಧ್ಯಂತರ ನಿಲ್ದಾಣಗಳಲ್ಲಿ ರೈಲು ನಿಲ್ಲುವ ಸಮಯವನ್ನು ಪರಿಗಣಿಸಿಲ್ಲ). ಎಕ್ಸ್ಪ್ರೆಸ್ ರೈಲಿನ ಸರಾಸರಿ ಜವವು ಪ್ಯಾಸೆಂಜರ್ ರೈಲಿನ ಸರಾಸರಿ ಜವಕ್ಕಿಂತ 11 km/h ಹೆಚ್ಚಾಗಿದ್ದರೆ, ಆ ಎರಡೂ ರೈಲುಗಳ ಸರಾಸರಿ ಜವವನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

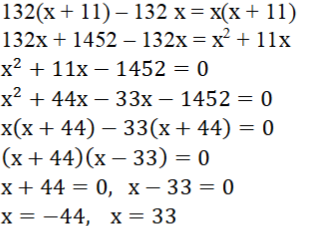
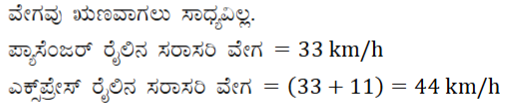
ಅಭ್ಯಾಸ 10.4
1. ಕೆಳಗಿನ ವರ್ಗಸಮೀಕರಣಗಳ ಮೂಲಗಳ ಸ್ವಭಾವವನ್ನು ವಿವೇಚಿಸಿ, ಅವು ವಾಸ್ತವ ಮೂಲಗಳಾಗಿದ್ದರೆ, ಅವುಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) 2x²-3x+5=0
(ii) 3x²-4√3x+4=0
(iii) 2x²-6x+3=0
ಉತ್ತರ :
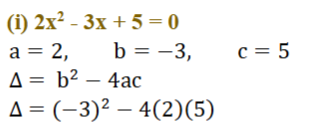


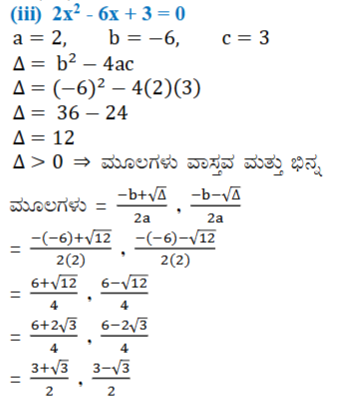
2. ಕೆಳಗಿನ ಪ್ರತಿಯೊಂದು ವರ್ಗ ಸಮೀಕರಣವು ಸಮನಾದ ಎರಡು ಮೂಲಗಳನ್ನು ಹೊಂದಿದ್ದರೆ k ಯ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
(i) 2x²+kx+3=0
(ii) kx (x-2)+6=0
ಉತ್ತರ:
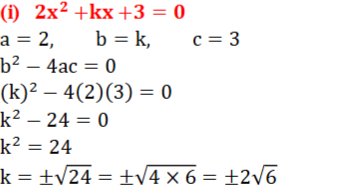
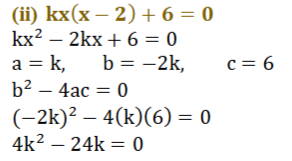
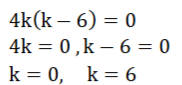
3. 800m² ವಿಸ್ತೀರ್ಣವುಳ್ಳ ಮತ್ತು ಉದ್ದವು ಅಗಲದ ಎರಡರಷ್ಟಿರುವ ಒಂದು ಆಯತಾಕಾರದ ಮಾವಿನ ತೋಪನ್ನು ನಿರ್ಮಿಸಲು ಸಾಧ್ಯವೇ? ಹೌದು ಎಂದಾದರೆ, ಅದರ ಉದ್ದ ಮತ್ತು ಆಗಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:

4. ಕೆಳಗೆ ಸೂಚಿಸಿರುವಂತಹ ಸನ್ನಿವೇಶವಿರಲು ಸಾಧ್ಯವೇ? ಹಾಗಿದ್ದರೆ ಅವರ ಈಗಿನ ವಯಸ್ಸುಗಳನ್ನು ನಿರ್ಧರಿಸಿ. ಇಬ್ಬರು ಸ್ನೇಹಿತರ ವಯಸ್ಸುಗಳ ಮೊತ್ತವು 20 ವರ್ಷಗಳಾಗಿವೆ. ನಾಲ್ಕು ವರ್ಷಗಳ ಹಿಂದೆ, ಅವರ ವಯಸ್ಸುಗಳ ಗುಣಲಬ್ಧವು 48 ವರ್ಷಗಳಾಗಿತ್ತು.
ಉತ್ತರ:

5. ಸುತ್ತಳತೆ 80m ಮತ್ತು ವಿಸ್ತೀರ್ಣ 400m² ಇರುವ ಒಂದು ಆಯತಾಕಾರದ ಉದ್ಯಾನವನವನ್ನು ನಿರ್ಮಿಸಲು ಸಾಧ್ಯವೇ? ಹೌದು ಎಂದಾದರೆ ಅದರ ಉದ್ದ ಮತ್ತು ಅಗಲಗಳನ್ನು ಕಂಡುಹಿಡಿಯಿರಿ.
ಉತ್ತರ:
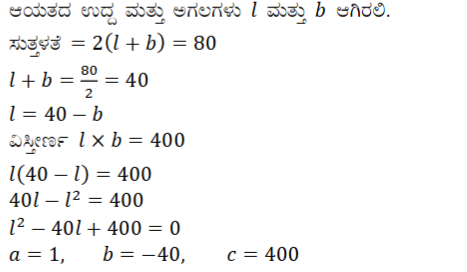

ನೆನಪಿನಲ್ಲಿಡ ಬೇಕಾದ ಅಂಶಗಳು
1. ಸಾಮಾನ್ಯವಾಗಿ, ax2 + bx + c = 0, a ≠ 0 ವರ್ಗ ಸಮೀಕರಣದಲ್ಲಿ ಒಂದು ವಾಸ್ತವ ಸಂಖ್ಯೆಗೆ α ಗೆ ax2 + bx + C =0 ಆದರೆ, ಆಗ α ವನ್ನು ಆ ವರ್ಗ ಸಮೀಕರಣದ ಒಂದು ಮೂಲ ಎನ್ನುತ್ತಾರೆ.
2. x = α ಎಂಬುದು ವರ್ಗ ಸಮೀಕರಣದ ಒಂದು ಪರಿಹಾರವಾಗಿದೆ ಅಥವಾ α ಇದು ವರ್ಗ ಸಮೀಕರಣವನ್ನು ಸರಿದೂಗಿಸುತ್ತದೆ ಎಂದೂ ನಾವು ಹೇಳುತ್ತೇವೆ. ax2 + bx + c ವರ್ಗ ಬಹುಪದೋಕ್ತಿಯ ಶೂನ್ಯತೆಗಳು ಮತ್ತು ax2 + bx + c = 0 ವರ್ಗ ಸಮೀಕರಣದ ಮೂಲಗಳು ಒಂದೇ ಆಗಿರುತ್ತವೆ.
3. b2 – 4ac < 0 ಆದರೆ, ಸಮೀಕರಣವು ವಾಸ್ತವ ಮೂಲಗಳನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ,
4. ಒಂದು ವರ್ಗ ಸಮೀಕರಣವನ್ನು ವರ್ಗ ಪೂರ್ಣಗೊಳಿಸುವ ವಿಧಾನದಿಂದಲೂ ಬಿಡಿಸಬಹುದು.
5. b2 – 4ac >= 0 ಆದರೆ ax2 + bx + c = 0 ವರ್ಗ ಸಮೀಕರಣದ ಮೂಲಗಳ
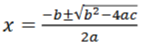
ಆಗಿರುತ್ತದೆ.
6. x2 + bx + c = 0 ವರ್ಗ ಸಮೀಕರಣವು
(i) b2 – 4ac > 0 ಆದರೆ ಎರಡು ಭಿನ್ನವಾದ ವಾಸ್ತವ ಮೂಲಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.
(ii) b2 – 4ac = 0 ಆದರೆ ಎರಡು ಸಮನಾದ ವಾಸ್ತವ ಮೂಲಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ.
(iii) b2 – 4ac < 0 ಆದರೆ ಯಾವುದೇ ವಾಸ್ತವ ಮೂಲಗಳನ್ನು ಹೊಂದಿರುವುದಿಲ್ಲ.
7. b2 – 4ac ಯ ಬೆಲೆಯು, ax2 + bx + c = 0 ವರ್ಗ ಸಮೀಕರಣದ ಮೂಲಗಳು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳಾಗಿವೆಯೇ ಅಥವಾ ಇಲ್ಲವೇ ಎಂಬುದನ್ನು ನಿರ್ಧರಿಸುವುದರಿಂದ b2 – 4ac ಯನ್ನು ವರ್ಗ ಸಮೀಕರಣದ ಶೋಧಕ ಎನ್ನುತ್ತಾರೆ.
8. ವರ್ಗ ಸಮೀಕರಣಗಳು ಚರಾಕ್ಷರವುಳ್ಳ ಒಂದು ವರ್ಗ ಸಮೀಕರಣವು ax2 + bx + c = 0 ರೂಪದ ಒಂದು ಸಮೀಕರಣವಾಗಿದ್ದು, ಇಲ್ಲಿ a,b,c ಗಳು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳು ಮತ್ತು a ≠ 0.
ಇತರೆ ವಿಷಯಗಳು :
ತ್ರಿಕೋನಮಿತಿಯ ಪ್ರಸ್ತಾವನೆ ನೋಟ್ಸ್
